2.1 Difrakce na rovinné pohlcující překážce

Základní teorie

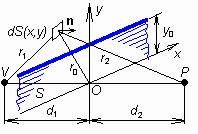
Obr. 2.1A.1

Difrakce na polorovině

Budeme se zabývat difrakcí vln v následující situaci. Mezi zdrojem vlnění V a místem příjmu P je tenká rovinná přepážka, která elektromagnetické vlny nepropouští ani neodráží (tzv. pohlcující přepážka). V přepážce je vyříznuto okénko nebo jiný otvor, kterým může vlnění procházet do oblasti místa příjmu. Přepážka může být také polorovinou, jak je nakresleno na obr. 2.1A.1 (okénkem je pak celá horní polorovina). Úkolem je vypočítat intenzitu pole v bodu P.

Popsaná situace je aproximací některých v praxi se vyskytujících úloh, např. šíření vln přes horský hřbet. Připomeňme, že při aplikacích v radiotechnice v souvislosti s šířením vln v terénu se místo termínu přepážka používá termín překážka (terénní překážka). Zde budeme používat oba termíny ve stejném významu.

Takto formulovanou úlohu řešil poprvé A.J. Fresnel (čti "Frenel", 1788 - 1827) poměrně jednoduchým způsobem, který nyní vysvětlíme. Pro Fresnelův způsob řešení difrakční úlohy se někdy používá termín Fresnelova difrakce.

Rovinu přepážky si označíme S a budeme předpokládat, že je kolmá na spojnici VP. Konkrétně budeme sledovat difrakci na přepážce - polorovině (obr. 2.1A.1), ale postup lze rozšířit i na jiné tvary okénka.

Nejprve vypočteme intenzitu pole E^(S) na rovině přepážky S tak, jakoby tam přepážka nebyla. Předpokládáme, že od zdroje V se šíří kulová vlna (obr. 2.1A.1), takže

E^{(S)} = C \frac{e^{- j k r_{1}}}{r_{1}}

( 2.1A.1 )

Zde C značí konstantu závislou na vyzařovaném výkonu zdroje a k je vlnové číslo.

Nyní použijeme Huygensův princip. Rovina S je zleva ozářena a každý její element dS je zdrojem záření pro poloprostor vpravo. Intenzita ozáření E^(S) je dána vztahem (2.1A.1) pro oblast od hrany přepážky nahoru (polorovina S₁), ale E^(S) = 0 od hrany přepážky směrem dolů, protože přepážka vlny nepropouští.

Každý element volné části roviny S můžeme tedy považovat za Huygensův zdroj ozářený vlnou s intenzitou (2.1A.1). Je už jen třeba sečíst intenzity vytvořené těmito zdroji v bodu P. S odvoláním na vztah pro intenzitu pole vytvořenou Huygensovým zdrojem (ozářenou ploškou) je:

E^{(P)} = \frac{j}{λ} \int_{S_{1}} E^{(S)} \cos (n, r_{2}) \frac{e^{- j k r_{2}}}{r_{2}} d S

( 2.1A.2 )

Integruje se po volné (propustné) části roviny S (v integrálu je formálně označena S₁). Po fyzikální stránce je problém vyřešen.

Aby Fresnel mohl matematicky vyřešit integrál (2.1A.2), musel přijmout některá zjednodušení. Všechna plynou z předpokladu, že největší podíl na intenzitě v bodě P mají ty Huygensovy zdroje, které leží blízko horní hrany přepážky, tedy i poměrně blízko počátku O (obr. 2.1A.1). Pro tyto zdroje úhel mezi normálou n k rovině přepážky a průvodičem r₂ k bodu příjmu je malý, a proto lze položit cos( n, r₂) = 1. Dále lze předpokládat, že souřadnice x, y jednotlivých Huygensových zdrojů jsou (číselně) malé vůči vzdálenostem d₁ a d₂. Pak, s odvoláním na pravidla počítání s malými čísly, přibližně platí:

r_{1} = \sqrt{d_{1}^{2} + x^{2} + y^{2}} = d_{1} \sqrt{1 + {(\frac{x}{d_{1}})}^{2} + {(\frac{y}{d_{1}})}^{2}} ≅ d_{1} [1 + \frac{1}{2} {(\frac{x}{d_{1}})}^{2} + \frac{1}{2} {(\frac{y}{d_{1}})}^{2}]

( 2.1A.3 )

Nakonec ještě ve jmenovatelích zlomků v (2.1A.1) a (2.1A.2) lze položit r₁ = d₁ a r₂ = d₂, protože tato zjednodušení pouze nepatrně ovlivní hodnotu amplitudy výsledné intenzity elektrického pole. Po těchto zjednodušeních se stane integrál (2.1A.2) řešitelným a jeho výsledek lze vyjádřit (pro jednodušší tvary okénka S₁ uzavřeným a nepříliš složitým vzorcem. Podrobnosti jsou uvedeny ve vrstvě B knihy.

Dnes lze řešit integrál (2.1A.2) numericky bez jakýchkoli zjednodušení. Až na malé výjimky se však numerický výpočet používá pouze při složitých tvarech okénka. Jedná-li se o difrakci na polorovině, je Fresnelovo (analytické) řešení jednoduché, přehledné a jeho přesnost dostačuje pro většinu aplikací.

Ještě si připomeňme - pro Fresnelovu difrakci jsou charakteristické tyto skutečnosti:

rovinná a pro vlny nepropustná přepážka,
aplikace Huygensova principu,
výše popsaná zjednodušení, přijatá pro analytické řešení integrálu.

Tvar propustného okénka může být různý.

Obr. 2.1A.2

Závislost intenzity |E(P)| na výšce překážky

V následujícím výkladu se omezíme na přepážku ve tvaru poloroviny, tedy situace nakreslené na obr. 2.1A.1. Výše popsaný postup umožňuje vypočítat intenzitu pole v bodě P v závislosti na vzdálenostech d₁ a d₂, výšce horní hrany přepážky y₀ (která může být i záporná, když přepážka končí pod spojnicí VP), na vlnové délce a na vlastnostech zdroje V. Aby vstupních veličin bylo méně, vztahuje se obvykle intenzita pole k intenzitě, která by byla v tomtéž místě bez přepážky; počítá se tedy poměr E (za přepážkou) / E (ve volném prostoru). Kromě toho ještě souřadnice horní hrany přepážky y₀ se neudává v délkových jednotkách, ale v poloměrech Fresnelových zón r_0n. Pak se výsledek stane nezávislý na konkrétních hodnotách d₁, d₂ a λ. Fresnelovy zóny na rovině překážky mají tvar mezikruží (hranice mezi sousedními zónami jsou kružnice se společným středem v průsečíku spojnice VP s rovinou překážky (O). Poloměry jednotlivých Fresnelových zón vypočítáme ze vzorce

r_{0 n} ≅ \sqrt{n} \sqrt{λ \frac{d_{1} d_{2}}{d_{1} + d_{2}}}

( 2.1A.4 )

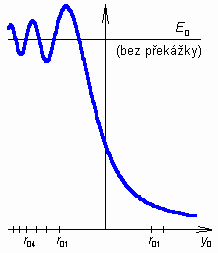
který platí s dobrou přesností, pokud vypočtený poloměr je malý vůči kterékoli vzdálenosti d₁ a d₂. Podrobněji je pojednáno o Fresnelových zónách ve vrstvě B.

Závislost relativní intenzity pole (E/E_vp) za překážkou na převýšení hrany překážky y₀ je nakreslena na obr. 2.1A.2. Všimněme si, že překážka ovlivňuje intenzitu pole v bodu P i tehdy, když y₀ je záporné a přímá spojnice VP není překážkou přerušena. Blíží-li se y₀ od záporných hodnot k nule, intenzita pole střídavě narůstá a zase klesá a amplituda kolísání se zvětšuje až téměř na 3 dB. Když y₀ = r₀₁/2 (mezi přímou spojnicí VP a hranou překážky zůstává volná přibližně polovina první Fresnelovy zóny), je intenzita pole ještě stejně velká jako ve volném prostoru bez překážky. Leží-li hrana překážky ještě blíže spojnici VP nebo dokonce nad ní (y₀ je kladné, spojnice VP je překážkou přerušena), překážka stíní a intenzita pole monotónně klesá. Při y₀ = 0 je E/E_vp = 1/2.

Střídavé narůstání a klesání intenzity pole při y₀ < 0 je zajímavý jev, který lze při pečlivé práci pozorovat i experimentálně, a to jak na rádiových, tak dokonce i na optických kmitočtech. V literatuře bývá vysvětlován střídavým zakrýváním a odkrýváním Fresnelových zón, ale to je nepřesné a málo názorné. Exaktní a názornější výklad je uveden ve vrstvě B. Příslušnou grafickou reprezentaci přináší program, popsaný ve vrstvě C.

Jako Fresnelova difrakce se v radiotechnice počítá intenzita pole za překážkami, které jsou poměrně úzké ve směru šíření vlny a které jsou protáhlé ve směru příčném. Mohou to být např. příčně protáhlé kopce (nebo ve větším měřítku horské hřbety), střechy budov ap. Pro číselnou představu uvažme např. rádiový spoj s délkou 40 km na frekvenci 600 MHz (V. televizní pásmo), který je na rušený příčnou překážkou uprostřed délky trasy. Poloměr první Fresnelovy zóny na rovině překážky je přibližně 70 m. Pokud tedy mezi vrcholem překážky a spojnicí VP zůstává mezera alespoň 35 m, pak překážka šíření vln ovlivní jen nepatrně. Tato mezera se nazývá světlost trasy. Když se spojnice VP právě dotýká vrcholu, nastává útlum 6 dB (na polovinu). Když vrchol leží např. 200 m nad spojnicí VP (to jsou přibližně 3 poloměry 1. Fresnelovy zóny), je útlum již téměř 26 dB (intenzita pole se sníží dvacetkrát). Další a podrobnější číselné údaje o útlumu a o velikosti Fresnelových zón v různých situacích nalezneme v programu, popsaném ve vrstvě C.

Nakonec ještě jedno upozornění. V okolí dobře vodivé překážky, (která elektromagnetické vlny nepropouští, nepohlcuje, ale odráží), jsou difrakční jevy poněkud jiné. Takovou situací se zabýváme v části 2.2.