2.1 Diffraction on a planar absorbing objectBasic theory
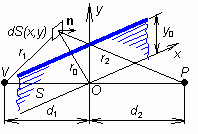
We are going to study the wave diffraction in the following situation. Between the wave source V and the observation point P, a thin planar object, which neither reflects nor transmits electromagnetic waves, (so called absorbing object) is placed. In the object, a small window is cut. Through the window, the wave can propagate from the source to the observation point. The object can have a form of a half-plane as depicted in fig. 2.1A.1 (the free upper half-plane plays the role of the window here). Computing the intensity in the observation point P is our task. The described situation approximates a certain category of practical problems (wave propagation behind a chine, e.g). For the first time, A. J. Fresnel (1788 - 1827) solved the above-formulated task. He elected a relatively simple approach we are going to explain now. The Fresnel solution is usually called the Fresnel diffraction. The plane of the object is signed S. The plane is assumed being perpendicular to the line VP. No matter the problem is solved for the half-plane (fig. 2.1A.1), the approach can be extended even to differently shaped windows. First, electric-field intensity E(S) is computed in the plane of the object S the same way as the object is absent. More, the spherical wave is assumed to propagate from the source V (fig. 2.1A.1), and therefore
Here, C is a constant dependent on the radiated power and k denotes wave number. Now, Huygens principle is applied. The plane S is left-illuminated and every its element dS is considered to be a radiation source for the right-hand half-space. Illumination intensity E(S) is given by eqn. (2.1A.1) for the region lying above the edge of the object (half-plane S1), but E(S) = 0 below the edge due to the absorption nature of the object. Each element of the free part of the plane S can be therefore considered as Huygens source illuminated by the wave of the intensity (2.1A.1). Now, we have to perform summation of field intensities created by those sources in the point P. Using the relation for the field intensity created by the Huygens source, we get
Integration is performed on the free (transmitting) part of the plane S (in the integral, we formally sign that as S1). From the physical point of view, the problem is solved out. In order to solve the integral (2.1A.2), Fresnel had to accept some simplifications. All these simplifications are based on the assumption that the most important contribution to the intensity in P is caused by the Huygens sources lying near to the upper edge of the object (i.e., even relatively near to the origin O as depicted in fig. 2.1A.1). For those source, the angle between the normal n to the object plane and the radius vector r2 to the observation point is small, and therefore, we can assume cos( n, r2) = 1. Next, the coordinates x, y of single Huygens sources can be assumed to be (numerically) small comparing to distances d1 and d2. Exploiting rules for small-numbers computation, we get
Finally, we assume r1 = d1 and r2 = d2 in the denominators of the fractions (2.1A.1) a (2.1A.2) because these assumptions negligibly influence the amplitude value of the total electric field intensity only. Performing these simplifications, the integral (2.1A.2) becomes solvable and the result can be expressed (for simpler shapes of the window S1) in closed, relatively simple form. The details are given in the layer B of the textbook. Using numerical methods, the integral (2.1A.2) can be solved without simplifications. Nevertheless, numerical methods are usually exploited in the case of complicated shapes of the window only. For the half-plane diffraction, the Fresnel (analytical) solution is simple, well understandable and its accuracy is sufficient for most applications. Let us remind the reader that the Fresnel diffraction considers:
The transmitting window can be of an arbitrary shape. In the following, we consider a half-plane object (fig. 2.1A.1).
Exploiting the above-described approach, the field intensity in the observation point P can be computed depending on the distances d1 and d2, on the upper-edge height y0 (which can be even negative if the edge is below the line VP), on the wavelength and on the source properties V. In order to reduce the number of input quantities, field intensity is usually related to the field intensity in the same point in the situation when the object is removed; we therefore compute the ratio E (behind the object) / E (in free space). Moreover, the upper-edge coordinate y0 is not given in meters but in Fresnel zone radii r0n. Then the result is independent on values of d1, d2 and λ. In the object plane, Fresnel zones are of the shape of annuli (the border between the neighboring zones are circles with the common center in the intersect of the line VP and the object plane (O). Fresnel zone radii can be computed according to
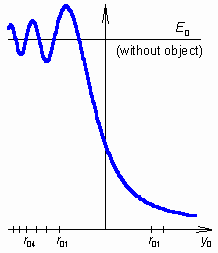
which accurate enough if the computed radius is small with respect to the distances d1 and d2. More detailed information about Fresnel zones is given in the layer B. Relative field-intensity (E/Evp) dependency on the edge height y0 is depicted in fig. 2.1A.2. We can see that the half-plane influences field-intensity in P even if y0 is negative and the line VP is not interrupted by the object. If y0 goes from negative values to zero, field intensity rises and drops down in cyclic way, and the variation amplitude increases up to nearly 3 dB. If y0 = r01/2 (approximately one half of the first Fresnel zone is free between the line VP and the edge), magnitude of the intensity is the same as in free space without objects. If the edge is nearer to the line VP or even above it (y0 is positive, the line VP is interrupted by the object), the object shades and the field intensity monotonously decreases. For y0 = 0, E/Evp = 1/2. A cyclic variation of field intensity for y0 < 0 is a rather interesting phenomenon, which can be observed even experimentally both on radio frequencies and on optical ones. In literature, a cyclic covering and uncovering Fresnel zones explain the phenomenon. Unfortunately, this explanation is not accurate and well understandable. Exact explanation is presented in the layer B. Graphical representation is provided by a program, which is introduced in the layer C. Finally, a small note. In the surrounding of a well conducting object, which does not transmit and absorb electromagnetic waves but reflect them, the diffraction phenomena are of different nature. This situation is described in the chapter 2.2. |