2.1 Difrakce na rovinné pohlcující překážcePodrobnější popis
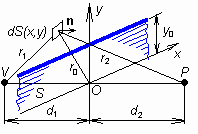
Za rovinnou překážku považujeme rovinu, která je kolmá ke spojnici VP (zdroj vlnění - bod pozorování), a která je zčásti pokryta materiálem, jenž elektromagnetické vlny dokonale pohlcuje (a tedy nepropouští). Zbývající část roviny je nepokryta, takže vlnění zde může volně procházet na odvrácenou stranu roviny, tedy do poloprostoru, kde leží bod pozorování P. Úkolem je vypočítat intenzitu pole v bodu P. S výjimkou případu, kdy je popsaná rovina celá volná, jedná se o difrakční úlohu. Klasickým řešením takto formulované úlohy je řešení Fresnelovo (Fresnelova difrakce). Fresnel uvažoval, že zdrojem vlnění pro poloprostor obsahující bod P je sama rovina překážky, resp. intenzita pole na její odvrácené straně. Na překážku se tedy Fresnel díval jako na velikou plošnou anténu. Fresnel dále předpokládal, že intenzita pole na odvrácené straně překážky je nulová v místech, kde překážka vlny nepropouští, a je nenulová a překážkou neovlivněná tam, kde překážka je volná. Oba předpoklady nejsou zcela přesné, ale většinou se jim skutečnost dobře blíží. Díky této představě se difrakční úloha řeší velmi pohodlně jako dvě samostatné navzájem nesouvisející běžné úlohy: šíření od zdroje na rovinu překážky a šíření od volných částí roviny překážky do bodu pozorování. Samotná překážka vlastně z výpočtu úplně vypadla a výsledek ovlivňuje jen tvarem propustných částí. Ve vrstvě A bylo naznačeno Fresnelovo řešení v situaci, kdy zakrytou částí roviny překážky je dolní polorovina a kdy volnou částí je polorovina horní (obr. 2.1B.1). Ze zdroje V se šíří kulová vlna, takže intenzita pole na rovině překážky je
v němž k je vlnové číslo, C je konstanta závislá na vyzařovaném výkonu a činiteli směrovosti vysílací antény, a kde vzdálenost r1 je dána vztahem . Symboly x, y označují souřadnice bodu na rovině překážky. Každý bod (x, y), resp. každý element dS = dxdy je ozářen zleva intenzitou (2.1B.1) a podle Huygensova principu je zdrojem vlnění pro oblast vpravo. K intenzitě pole v bodě P přispívá příspěvkem . Integrací všech příspěvků po volné části roviny překážky (tj. po horní polorovině v mezích -∞ < x < +∞, y0 < y < +∞) získáme výslednou intenzitu pole v bodě P, a tedy cílové řešení úlohy:
Připomeňme na tomto místě, že při jiném tvaru volné části roviny překážky změní se pouze meze integrace. Aby bylo možné výpočet bez potíží dokončit, přijal Fresnel některá zjednodušení, která jsou pro jeho postup charakteristická. Vesměs vycházejí z předpokladu, že hlavní podíl na intenzitě pole v bodě P mají elementární zdroje dxdy, ležící blízko přímé spojnice VP, tedy elementy, jejichž souřadnice vyhovují nerovnostem x << d1,2 a y << d1,2. Pak lze položit cos(n,r2) = 1 a ve jmenovatelích r 1 = d1, r2 = d2. Ve fázových činitelích musíme vyjádřit vzdálenosti r1 a r2 přesněji:
Po těchto úpravách má výsledný vztah tvar
kde
Protože v integrandu (2.1B.4) je každý činitel funkcí jen jedné proměnné, stačí k integraci znát řešení integrálu typu . Substitucí
převedeme tento integrál na Fresnelovy integrály
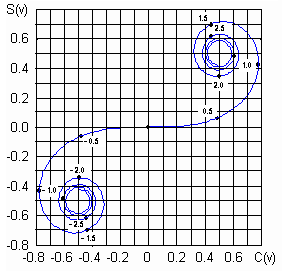
Hodnoty Fresnelových integrálů C(v) a S(v) jsou tabelovány, jsou v knihovnách některých počítačových jazyků a jsou také souřadnicemi křivky nakreslené na obr. 2.1B.2. Křivka se nazývá klothoida. Čísla na křivce jsou hodnoty argumentu v a příslušné hodnoty integrálů C(v) a S(v) čteme na osách. Pravá (horní) větev končí v bodě C(v=∞) = 0.5, S(v=∞) = 0.5 a levá větev je souměrná podle počátku. Konečné řešení úlohy má tvar
Závislost intenzity pole v bodě P (za překážkou) na výšce překážky y0 byla diskutována ve vrstvě A učebnice. Zde pouze připomeneme, že překážka ovlivňuje šíření, i když přímá spojnice VP není přerušena, a že v takovém případě může překážka způsobit i mírný vzestup intenzity vůči trase bez překážky. Teprve když mezera mezi vrcholem překážky a spojnicí VP (tzv. světlost trasy) se zmenší pod polovinu první Fresnelovy zóny, začne intenzita pole za překážkou klesat pod úroveň, odpovídající volnému prostoru. Protože v integrandu integrálu (2.1B.4) je každý činitel funkcí jen jedné proměnné, můžeme tento integrál zapsat jako součin dvou samostatných integrálů: jeden podle dx, druhý podle dy. Integrál podle dx má nekonečné meze, jeho hodnota nezávisí na výšce překážky a je pro danou situaci konstantou. To znamená, že intenzita pole v bodě P je úměrná pouze hodnotě integrálu podle y a tedy, s využitím substituce (2.1B.6), integrálu
Pravou stranu (2.1B.9) snadno vyložíme jako rozdíl dvou komplexních čísel v komplexní rovině C(v), jS(v), tedy i v rovině klothoidy na obr. 2.1B.2, kde svislou osu považujeme za její osu imaginární. Rozdíl souřadnic dvou bodů v komplexní rovině je, jak známo, roven délce úsečky z jednoho bodu do druhého. Poslední krátkou úvahu můžeme tedy uzavřít následujícím zjištěním: intenzita pole v bodě P je úměrná délce úsečky z bodu [C(v0), S(v0)] do bodu [C(∞), S(∞)] na klothoidě. Bod [C(∞), S(∞)] je bod se souřadnicemi 0.5, 0.5 a je pevný. Když si představíme, že vrchol překážky se postupně zdola přibližuje přímé spojnici VP (a trasa je ještě volná), bod [C(v0), S(v0)] leží na levé (dolní) větvi klothoidy. Jak se překážka zvyšuje, posunuje se tento bod po jednotlivých závitech křivky směrem k počátku a délka spojnice obou inkriminovaných bodů střídavě narůstá a klesá. Proto se také intenzita pole v bodě P střídavě zvětšuje a zmenšuje. Až když se bod [C(v0), S(v0)] přiblíží počátku natolik, že se dostane za poslední (vnější) závit levé větve, oscilace přestanou a délka úsečky i intenzita pole monotónně klesají. Uvedené skutečnosti demonstruje program, popsaný ve vrstvě C , ve kterém lze sledovat pro zvolenou konkrétní rádiovou trasu kvantitativní údaje, týkající se útlumu, souvislosti útlumu se světlostí trasy a postupným zakrýváním Fresnelových zón na rovině překážky. Pro ilustraci vlivu Fresnelových zón na intenzitu pole za překážkou se vraťme ještě k obecnému výsledku (2.1B.2). Místo souřadnic x, y plošky dS zaveďme radiální vzdálenost plošky od počátku. Pak je
Vidíme, že příspěvky plošek různě vzdálených od počátku mají různou fázi (-ar02). V odstupu vzdáleností r01, r02, ... r0n určených rovnicí
se mění (zpožďuje se) fáze o 180°. Příčinou je prodlužování lomené spojnice V - dS - P vždy o l /2. Poloměry r0n v rovnici (2.1B.11) jsou tedy poloměry vnější hranice jednotlivých Fresnelových zón. Skutečně, po dosazení za a ze vztahu (2.1B.5) do (2.1B.11) obdržíme výsledek shodný s (2.1A.4). Skutečnost, že fáze příspěvků ze sousedních Fresnelových zón (na rovině S) se liší o 180° (a tudíž, že jejich příspěvky se navzájem ruší), má zajímavé důsledky. Trochu pozměňme výše řešenou úlohu. Představme si, že nepropustná přepážka zakrývá celou rovinu S. Máme však možnost vyříznout v ní kruhový otvor se středem v O a s libovolným poloměrem r0. Tímto otvorem prochází vlnění do bodu P. K výpočtu intenzity E(P) vyjdeme ze vztahu (2.1B.10) a vzhledem k rotační symetrii otvoru použijeme při integraci na rovině S polárních souřadnic: dS = r0 djdr 0. Integrujeme po ploše otvoru:
Integrál je snadno řešitelný substitucí r02 = r. Označíme-li
intenzitu pole v P ve volném prostoru (bez přepážky), pro různé poloměry otvoru r0 dostaneme následující konkrétní výsledky:
Na první pohled se zdá, že intenzita pole E0, kterou zjistíme v bodě P při zcela volném prostoru (bez přepážky), je tam proto, že je volná část (přibližně polovina) první Fresnelovy zóny, a že příspěvky všech ostatních zón, (které jsou také volné), se navzájem ruší. To je ale závěr nesprávný přinejmenším proto, že nelze říci, část které Fresnelovy zóny dává právě ten příspěvek, který se neruší s ostatními. Přesto však účelným zakrýváním jednotlivých zón lze vzájemné rušení potlačit a intenzitu pole v bodě P zvětšit. Tak například přepážka ve tvaru soustředných mezikruží, které by zakryly všechny sudé (anebo všechny liché) Fresnelovy zóny způsobí, že intenzita pole E(P) = ∞. Výsledek je sice překvapující, ale není ani chybný ani akademický. Taková překážka působí totiž jako spojná čočka (Fresnelova destička) a bod P je jejím ohniskem, do něhož je koncentrováno (se stejnou fází) veškeré vlnění, které ze zdroje na přepážku dopadá. |