2.2 Obecná teorie difrakceZákladní teorieFresnelova difrakce dává správné výsledky jen když překážka je rovinná, tenká a když vlny neodráží (je pohlcující). Ohybové jevy na trojrozměrných tělesech se musí počítat jinak. Seznámíme se s hlavními kroky obecného řešení difrakční úlohy.
Těleso známého tvaru a známých elektrických vlastností (permitivita, měrná vodivost ap.) je ozařováno vlnou, jejíž intenzitu v každém bodě prostoru známe. To je tzv. primární vlna, primární vlnění. Působením primární vlny se těleso polarizuje (je-li dielektrické) anebo se na jeho povrchu indukují proudy, je-li vodivé. V důsledku polarizace či indukovaných proudů se stává samo zdrojem nového vlnění; to je tzv. sekundární vlnění, sekundární vlna. Ta se šíří od tělesa všemi směry. Výsledná intenzita pole kdekoli v okolí tělesa (i za ním) je součtem intenzity primární a sekundární vlny. Matematické vyjádření sekundárního vlnění nalezneme řešením homogenní vlnové rovnice a velikost sekundárního vlnění se určí z požadavku, aby výsledná intenzita pole na povrchu tělesa (součet intenzit primární a sekundární vlny) splňovala okrajovou podmínku. Postup řešení ukážeme na příkladu. Půjde o difrakci rovinné vlny na nekonečně dlouhém, dokonale vodivém kruhovém válci. Řez válcem je nakreslen na obr. 2.2A.1. Jeho osa je totožná s osou z kartézské soustavy, jeho poloměr je a. Válec je ozařován rovinnou vlnou, jež přichází zprava (šíří se směrem -x) a má jen složku Ez: Ez prim = E0exp(jkx). Protože ve všech řezech rovnoběžných s rovinou xy je situace stejná, řešíme úlohu jako dvojrozměrnou. V dalším bude třeba přejít od kartézské soustavy x, y k soustavě polární r, φ (obr. 2.2A.1). Proto ve výše uvedeném vztahu dosadíme x = r cos(φ). Intenzita pole ozařující (tj. primární) vlny je tudíž
Tato vlna budí na povrchu válce proudy, které jsou zdrojem sekundárního vlnění. O indukovaných proudech nevíme v tuto chvíli nic. Víme však, že sekundární vlnění musí vyhovovat homogenní vlnové rovnici. Její obecné řešení má tvar
Zde m je separační konstanta, Am jsou integrační konstanty a Hm(2)(kr) je Hankelova funkce m-tého řádu druhého druhu argumentu (kr). Protože po každé otočce o 360 stupňů ve směru φ se hodnoty intenzity pole opakují, musí být konstanta m číslo celé a sčítání (2.2A.2) probíhá pro všechna celá m. Odvození (2.2A.2) je uvedeno ve vrstvě B. Zbývá ještě nalézt integrační konstanty Am. K tomuto cíli poslouží okrajová podmínka: tečná složka výsledné intenzity pole na povrchu dokonale vodivého válce musí být nulová. Protože sama složka Ez je tečná, musí platit
Po dosazení ze vztahů (2.2A.1) a (2.2A.2) do (2.2A.3) a po několika matematických úpravách lze získat následující vztahy pro integrační konstanty Am:
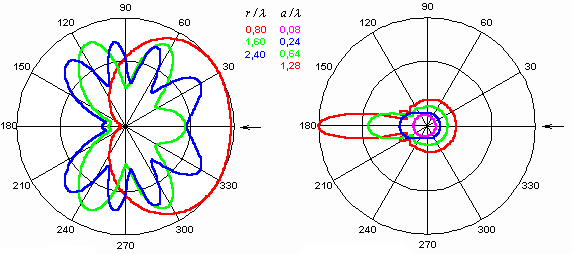
Ve výše uvedeném vztahu značí E0 amplitudu primární vlny, k je vlnové číslo prostředí, v němž se válec nachází, a je poloměr válce, Jm(ka) Besselova funkce m-tého řádu argumentu ka, Hm(2)(kr) je Hankelova funkce m-tého řádu druhého druhu argumentu (ka) a j je imaginární jednotka. Odvození je uvedeno ve vrstvě B. Výsledná intenzita v okolí válce je rovna součtu intenzit primární a sekundární vlny. Výsledek vychází ve tvaru nekonečné řady – sekundární vlna (2.2A.2) v součtu s vlnou primární (2.2A.1). Tím je řešení úlohy dokončeno. V aplikacích je někdy potřeba zabývat se ještě urychlením konvergence výsledné řady. Obraťme nyní pozornost ke struktuře vlnění v okolí válce. Ta je složitá. Radiálně od válce se šíří válcové vlny určené řadou (2.2A.2). Ty interferují s primární rovinnou vlnou, takže v okolí existuje jak postupné, tak i stojaté vlnění. Každý radiální směr svírá jiný úhel se směrem šíření primární vlny, a proto délka stojatého vlnění je v každém směru jiná. Důsledkem je skutečnost, že směrové charakteristiky pozorované v různých vzdálenostech od válce se liší. Příklady vidíme na obr. 2.2A.2. Směr šíření dopadající vlny je označen šipkou. Vlevo jsou charakteristiky výsledného vlnění, vpravo charakteristiky samotného sekundárního vlnění. Je zajímavé, že sekundární vlnění má maximum ve směru za válec.
Strukturu vlnění v okolí vodivého válce si můžeme podrobněji prohlédnout pomocí programů pro matlab. První z nich zobrazuje směrové charakteristiky jak samotného sekundárního vlnění tak i vlnění výsledného, pozorované v různých vzdálenostech od osy válce. Druhý program ukazuje, jak vypadá výsledné (stojaté) vlnění v různých radiálních směrech. Programy a další podrobnosti k nim jsou uvedeny ve vrstvě C. Dnes je známo řešení difrakční úlohy pro různá geometricky jednoduchá tělesa. Praktický význam má řešení pro obecný (trojosý) elipsoid; volbou poloos lze aproximovat některé technicky užitečné tvary. Při a = b = c přechází elipsoid v kouli. Když a = b << c, je elipsoid protáhlý a aproximuje válcový vodič konečné délky. Když naopak a = b >> c, je jeho tvar blízký kruhové destičce. Na závěr ještě jednu poznámku. Při řešení difrakce na válci jsme předpokládali, že primární vlnění samo existuje všude v prostoru, tedy i za válcem. Tedy i za válcem na odvrácené straně musí být splněna okrajová podmínka (2.2A.3). Tato drobnost, která se snadno přehlédne, umožnila začátkem 20. století řešit mnohé difrakční problémy, tehdy důležité pro rozvoj radiotechniky. | ||||||||||||||||||||||||