2.2 General Theory of diffractionBasic theoryFresnel diffraction gives correct results for planar, thin and absorbing obstacles only. Diffraction phenomena on three-dimensional objects have to be therefore computed a different way. Hence, we have to study the basic steps of the general solution of diffraction tasks.
An objects of a known shape and of known electrical properties (permittivity, conductivity, etc.) is illuminated by a wave, which intensity is known in every point of the environment. This is so called primary wave. Reacting to the primary wave, the object is polarized (if the object is of dielectric nature) or currents are induced on the surface of the object (if the object is conductive). As a cause of polarization or current induction, the object becomes a source of a new wave (secondary wave). The secondary wave propagates in all the directions from the object. The total field intensity in the object surrounding (even behind the object) is then given by the summation of the primary wave and secondary one. Mathematical description of the secondary wave can be obtained by solving homogeneous wave equation. Magnitude of the secondary wave can be determined from the requirement that the total field intensity on the object surface (summation of the primary wave and the secondary one) meets the boundary condition. The algorithm of the solution is shown on an example. We are going to compute plane-wave diffraction on an infinitely long perfectly conducting circular cylinder. The cross-section of the cylinder is depicted in figure 2.2A.1. The cylinder axis identical with the z axis of the
Cartesian coordinate system,
the cylinder radius is denoted as a. The cylinder is illuminated by the
plane wave
propagating in the direction -x and consisting of the component:
This wave excites currents on the surface of the cylinder, which act as sources of the secondary wave. Dealing with induced currents, we do not have any information about them now. We know only that the secondary wave has to meet the homogeneous wave equation . Its general solution is of the form
Here, m is a separation constant, Am are integration constants and Hm(2)(kr) is Hankel function of order m of second kind and of the argument (kr). After the rotation for 360 degrees in the direction φ, values of the field intensity have to repeat, and therefore, the constant m is integer number and summation (2.2A.2) is performed for all the integer m. Derivation of (2.2A.2) is given in the layer B. Finally, values of the integration constants Am have to be found. To reach that, the boundary condition has to be applied: tangential component of the total field intensity on the surface of perfectly conducting cylinder has to be zero. Since Ez is tangential, we get
Substituting (2.2A.1) and (2.2A.2) to (2.2A.3) and performing several mathematical re-arrangements, we get relations for computing integration constants Am:
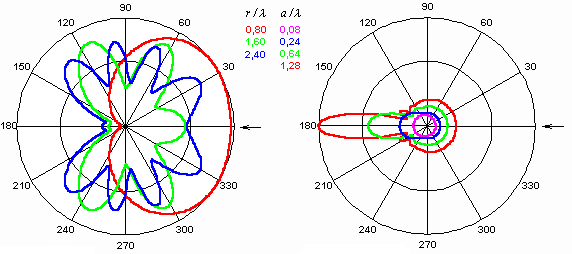
In the above-given relation, E0 denotes the primary wave amplitude, k is wave-number of the environment containing the cylinder, a is radius of the cylinder, Jm(ka) is Bessel function of order m and of the argument ka, Hm(2)(kr) is Hankel function of order m of second kind and of the argument (ka) and j denotes imaginary unit. Derivation is given in the layer B. The total intensity in the surrounding of the cylinder equals to the summation of the primary wave intensity and the secondary one. The result is obtained in the form of an infinite series - the secondary wave (2.2A.2) summed with the primary one (2.2A.1). That way, the solution is finished. In applications, even the speeding-up the convergence of the final series has to be solved. Now, turn our attention to the structure of the wave in the surrounding of the cylinder. The structure is complicated. In the radial direction, cylindrical waves given by (2.2A.2) propagate. These waves interfere with the primary wave, and therefore, both the traveling wave, and the standing one exist in the surrounding of the cylinder. Since each radial direction contains a different angle with the propagation direction of the primary wave, the standing-wave wavelength is different in every direction. As a result, directivity patterns in different distances are different as shown in fig. 2.2A.2. In this figure, the propagation direction of an incident wave is indicated by an arrow. In the left, directivity patterns of the total wave is depicted, in the right, directivity patterns of only secondary wave are shown. Surprisingly, the maximum of the secondary wave is in the direction behind the cylinder.
The wave structure near the conducting cylinder can be observed using matlab programs. The first program displays directivity patterns of both the single secondary wave and the total wave, which are observed in various distances from the cylinder axis. The second program shows the total (standing) wave in various radial directions. Programs are described in the layer C. Today, solution of the diffraction task is known for various geometrically simple objects. From the practical point of view, the solution for a general ellipsoid is of great importance because the proper choice of the half-axis length enables to approximate technically useful shapes. For a = b = c the ellipsoid becomes a sphere. For a = b << c the ellipsoid approximates a cylindrical conductor of a finite length. For a = b >> c the ellipsoid approaches a circular slab. Finally, a small note. During the solution of the diffraction on the cylinder, the primary wave was assumed to exist everywhere in the space, i.e. even behind the cylinder. I.e. even behind the cylinder on the reverse side, the boundary condition (2.2A.3) has to be fulfilled. This fact enabled to solve many diffraction problems at the beginning of the 20th century, which was very important for the development of radio electronics. | ||||||||||||||||||||||||