2.2 Obecná teorie difrakcePodrobnější popisSeznámíme se nyní s teorií, umožňující analyticky řešit difrakční úlohy na tělesech obecnějších tvarů. Jak však uvidíme, obecnost řešení se týká pouze fyzikálního přístupu. Z formálních (matematických) důvodů je dále popsaný postup prakticky použitelný jen pro tělesa, která mají jednoduchý geometrický tvar.
Jak již bylo řečeno ve vrstvě A, fyzikální princip řešení je následující. V okolí tělesa existuje známé, tzv. primární vlnění, kterým je těleso ozařováno. V důsledku ozáření (např. v důsledku v tělese indukovaných proudů) je těleso samo zdrojem vlastního, tzv. sekundárního vlnění. To se šíří od tělesa všemi směry. Výsledná intenzita pole v okolí tělesa (v prostoru) je součtem intenzit polí primárního a sekundárního vlnění. Protože intenzita primárního vlnění je známá, stačí nějak zjistit intenzitu vlnění sekundárního. K tomu nám dopomohou dvě podmínky:
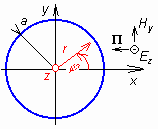
Až sem se zdá všechno jednoduché, celkem jasné a téměř samozřejmé. Ovšem konkrétní postup přináší (jako obvykle) některé záludnosti. Proto si nyní popíšeme bez větších matematických skoků řešení difrakce rovinné vlny na nekonečně dlouhém, dokonale vodivém kruhovém válci. Řez válcem je nakreslen na obr. 2.2B.1. Osa válce je totožná s osou z kartézské souřadné soustavy, poloměr válce je a. Válec je ozařován rovinnou vlnou přicházející zprava (šíří se směrem -x) a vektor E má jen složku Ez (je tedy tečný k povrchu válce). Protože ve všech řezech rovnoběžných s rovinou xy je situace stejná, můžeme řešit úlohu jako dvourozměrnou. Vzhledem k osové symetrii povrchu válce použijeme při řešení válcovou souřadnou soustavu, v rovinném řezu pak polární souřadnice r, φ (viz obr. 2.2B.1). Je zřejmé, že platí x = r cos(φ). Intenzita pole primárního vlnění je podle předchozího
Intenzita pole sekundárního vlnění musí vyhovovat vlnové rovnici
Rozepíšeme-li operátor ∇2 pro válcovou souřadnou soustavu [1] a položíme-li d/dz = 0, získáme rovnici
Rovnici budeme řešit separací proměnných. Položíme Ez = R(r) Φ(φ) a dosadíme do (2.2B.3), přičemž pro derivaci podle φ je R konstantou a naopak. Pak rovnici dělíme součinem RΦ a snadno osamostatníme člen, obsahující pouze φ a Φ, zatímco ostatní členy obsahují pouze r a R. Rovnice je tedy separována. Má-li rovnice platit pro jakoukoliv kombinaci proměnných r a φ, musí být každá z obou separovaných částí rovnice konstantní. Člen obsahující pouze φ a Φ položíme roven –m2, kde m je tzv. separační konstanta. Tak získáme rovnici
Rovnice (2.2B.4) je diferenciální rovnice druhého řádu s konstantními koeficienty (m). Řeší se pomocí charakteristické rovnice a výsledek lze vyjádřit buď exponenciálními nebo goniometrickými funkcemi. Protože výsledek, tj. funkce Φ(φ), udává závislost intenzity pole na souřadnici φ, tj. dokola kolem osy válce, a protože v tomto směru nepředpokládáme šíření vlny, použijeme funkce goniometrické:
A a B, resp. C a φ0 jsou integrační konstanty. Zde dáme přednost poslednímu tvaru, v němž konstanta φ0 závisí pouze na tom, od jakého směru měříme úhel φ. Vzhledem k osové symetrii válce můžeme volit směr φ = 0 libovolně a proto položíme φ0 = 0. Konečný vztah se tak formálně zjednoduší. Ještě jeden důležitý poznatek vyplývá z rovnice (2.2B.5). Změní-li se úhel φ o 2π, dostaneme se do stejného bodu v prostoru, takže se vrátíme do stejné intenzity pole, a tedy i ke stejné hodnotě funkce Φ. A to je možné jen tehdy, je-li separační konstanta m číslo celé. Nyní obrátíme pozornost k druhé části separované rovnice (2.2B.3), obsahující proměnné r a R. Ta má nyní tvar
Substitucí ρ = kr a po drobných úpravách ji snadno převedeme na rovnici Besselovu:
Protože konstanta m je celé číslo, je řešením Besselovy rovnice buď lineární kombinace Besselových a Neumannových funkcí nebo lineární kombinace Hankelových funkcí prvního a druhého druhu. Protože funkce R udává závislost intenzity pole na radiální souřadnici r (směrem od válce) a v tom směru se vlnění šíří, dáme přednost Hankelovým funkcím. A protože Hankelova funkce prvního druhu popisuje vlnění šířící se z nekonečna ke svému zdroji a Hankelova funkce druhého druhu naopak popisuje vlnění šířící se od zdroje pryč, použijeme pouze funkci druhého druhu. Spojíme-li řešení rovnic (2.2B.4) a (2.2B.7), získáme obecný integrál rovnice (2.2B.3):
Rovnici (2.2B.3) vyhovuje řešení (2.2B.8) pro každé celé m. Protože to správné m zatím neznáme, musíme připustit řešení pro všechny možné hodnoty separační konstanty m a také libovolnou lineární kombinaci těchto řešení. Konečný výsledek řešení rovnice (2.2B.3) zapíšeme ve tvaru nekonečné řady
Výsledek (2.2B.9) si můžeme vyložit tak, že od válce se šíří soubor nekonečného počtu vln, které dohromady skládají sekundární vlnění. Každý sčítanec řady (2.2B.9) představuje jednu z těchto dílčích vln. Tyto vlny se navzájem liší svými amplitudami (to jsou zatím neznámé koeficienty Am), závislostí na radiální vzdálenosti r (koeficient Hm(2)(kr) závisí na m) a také závislostí na φ, tedy na směru od válce. Vlna pro m = 0 se šíří všemi směry se stejnou amplitudou cos(mφ) = cos(0) = 1 = konst., vlna pro m = 1 vykazuje osmičkovou směrovou charakteristiku (maximum pro φ = 0, π; nulová amplituda pro φ = ±π/2), atd. V tuto chvíli se zdá, že se všechno trochu komplikuje. Ale je to právě ta nekonečná řada (2.2B.9), která umožní řešení úspěšně dokončit. Účelnou volbou koeficientů Am můžeme totiž téměř vždy dosáhnout toho, aby řada (2.2B.9) jako celek splnila právě ty okrajové podmínky, které musí být splněny na povrchu tělesa (je to podobné jako třeba u Fourierovy řady: správnou volbou koeficientů u jednotlivých složek můžeme vyjádřit téměř jakýkoli časový průběh signálu). Pro dokonale vodivý a nekonečně dlouhý válec je formulace okrajové podmínky jednoduchá: tečná složka výsledné intenzity pole na plášti musí být nulová. Protože v našem případě má vlnění jen složku Ez, a ta je tečná, musí být
a po dosazení z rovnic (2.2B.1) a (2.2B.9), je
Z této rovnice musíme vypočítat zatím neznámé koeficienty Am. Máme ovšem k dispozici pouze jedinou rovnici pro nekonečný počet koeficientů. V podobných situacích vede někdy k cíli metoda neurčitých součinitelů ([1], [4]). Ta ale vyžaduje, aby všechny sčítance (v našem případě oba sčítance) v rovnici (2.2B.11) byly vyjádřeny řadou stejného typu (v našem případě řadou, obsahující členy cos(mφ). Pokud tomu tak je, pak stačí do příslušné rovnice postupně dosazovat m = 0, 1, 2, ... ∞ a z jediné rovnice získáme tak nekonečně mnoho rovnic pro koeficienty (součinitele) Am. Na štěstí pro nás je známý rozvoj
který dovoluje rozvinout primární vlnění v řadu se členy typu cos(mφ). Rozvoj dosadíme do (2.2B.11) a postupně srovnáváme koeficienty stojící u cos(φ), cos(2φ), cos(3φ) atd. Tak získáme vztahy
a z nich
Tím je analytické řešení úlohy dokončeno. Nejprve vypočteme koeficienty Am a pak samotné sekundární vlnění je dáno řadou (2.2B.9). Výsledné intenzity pole v okolí válce získáme součtem intenzit sekundárního vlnění (2.2B.9) a primárního vlnění (2.2B.1). Ještě si připomeňme podmínky, za kterých je popsaná metoda úspěšná. Především tvar tělesa musí být jednoduchý; jeho povrch musí být souřadnou plochou v nějaké souřadné soustavě, ve které umíme vyřešit vlnovou rovnici (2.2B.2). Druhou podmínkou je znalost rozvoje primárního vlnění v řadu téhož typu, jakou dostáváme při řešení vlnové rovnice. A konečně v praxi může sehrát určitou roli ještě další podmínka: řada pro sekundární vlnění musí přiměřeně rychle konvergovat. S konvergencí vznikají nesnáze v situacích, kdy rozměry tělesa jsou o několik řádů větší, než je vlnová délka. Např. když počítáme difrakci velmi krátkých (rádiových) vln na povrchu zeměkoule, pak k dostatečně přesnému vyjádření sekundárního pole v některých místech by bylo třeba sčítat desítky a stovky miliónů členů řady. Dnes je známo řešení difrakční úlohy pro různá geometricky jednoduchá tělesa: kouli, válec (kruhový, eliptický, parabolický) a pro obecný (trojosý) elipsoid; volbou jeho poloos (a, b, c) lze dobře aproximovat některé technicky užitečné tvary. Při a = b = c přechází elipsoid v kouli. Když a = b << c, je elipsoid protáhlý a aproximuje válcový vodič konečné délky (popřípadě dlouhý pásek, když a << b << c). Když naopak a = b >> c, je tvar elipsoidu blízký kruhové destičce. Struktura vlnění v okolí válce byla stručně komentována ve vrstvě A. V okolí válce existuje jak postupné, tak stojaté vlnění, které vzniká skládáním vlnění primárního a sekundárního. Protože tato vlnění mají různý směr šíření a protože se poněkud liší i jejich fázové rychlosti, jsou délky stojatého vlnění v různých směrech od válce různé. Je zajímavé, že samotné sekundární vlnění má největší intenzitu ve směru za válec. Pokud poloměr válce je menší než asi 1/10 vlnové délky, je vliv válce na primární vlnění malý. Podrobněji se můžeme seznámit se strukturou vlnění pomocí počítačových programů (viz vrstva C). První program zobrazuje intenzity pole sekundárního a výsledného vlnění v okolí válce v polárních souřadnicích formou směrových charakteristik. Sledují se intenzity pole v různých směrech v konstantní vzdálenosti od osy válce. Druhý program zobrazuje rozložení intenzit polí podél radiálních přímek vedených v různých směrech. Podrobnější výklad je ve vrstvě C. Na závěr ještě stručnou zmínku k řešení difrakční úlohy v případě, kdy vodivost válce není nekonečná nebo když jde o dielektrický válec. V takovém případě se musí vlnová rovnice (2.2B.2) vyřešit i pro oblast uvnitř válce. Tam se vlny nešíří, je tam stojaté vlnění. Proto pro řešení vlnové rovnice nepoužijeme funkce Hankelovy, ale funkce Besselovy a Neumannovy. A protože ještě pro r = 0 (tj. na ose válce) Neumannova funkce nabývá nekonečné hodnoty, zatímco intenzita pole tam musí být konečná, musíme tuto funkci z řešení vyloučit. V analogii k (2.2B.9) platí tedy pro oblast uvnitř válce:
Pro určení koeficientů řady má okrajová podmínka tvar
I zde je nutné vyjádřit všechny intenzity řadami téhož typu, a pak se aplikuje metoda neurčitých součinitelů [4]. Protože se zde vyskytují dva nekonečné soubory neznámých součinitelů (Am, Bm), tak samotná podmínka (2.2B.16) nestačí. Řešení je nutné opakovat ještě pro magnetické pole včetně příslušné okrajové podmínky. |