2.3 Geometrická optika

Základní teorie

Fresnelova teorie difrakce je jednoduchá, ale umí řešit jen tenké rovinné překážky. Obecná teorie, popsaná v čl. 2.2, je formálně složitá a výběr těles je značně limitovaný nejen geometrickou jednoduchostí, ale i dalšími požadavky. Proto se hledaly jiné cesty. Jednou z nich je Geometrická teorie difrakce (GTD), která numerickou cestou s pomocí počítače zvládne i složité situace. Před výkladem podstaty GTD se seznámíme se základními pojmy geometrické optiky(GO).

Současná geometrická optika je účinná metoda pro řešení vlnových dějů (šíření vln) ve složitějších prostředích. Není omezená na oblast optických frekvencí a lze ji použít i na rádiových vlnách. Od klasické geometrické optiky převzala představu o šíření vln podél paprsků, avšak umožňuje počítat nejen dráhy (trajektorie) vln, ale i změny intenzity pole a polarizace vln při šíření. Teorie GO vychází ze dvou předpokladů:

Vlnová délka je malá, takže vlnové číslo k je velké.
Vlnění sledujeme daleko od zdroje, takže jeho amplituda se mění ve směru šíření jen pozvolna, ale jeho fáze se mění rychle. Smysl tohoto požadavku si nejlépe uvědomíme na jednoduchém číselném příkladu: zajímáme se např. o šíření kulové vlny ve vzdálenosti deseti vlnových délek od zdroje; zvětší-li se vzdálenost třeba o polovinu vlnové délky, tj. o 5 %, zmenší se amplituda intenzity přibližně také o 5 % (málo), ale fáze se změní o π (podstatně).

Výklad GO začneme tím, že poněkud pozměníme dosud používaný vztah pro intenzitu pole elektromagnetické vlny. Místo E = E_m exp(-jkr) budeme psát

E = E_{m} \exp [- j k_{0} L (x, y, z)]

( 2.3A.1 )

V exponentu bude vždy k₀ = ω (ε₀μ₀)^1/2 a parametry prostředí budou zahrnuty ve funkci L. Snadno domyslíme, že L( x, y, z) = konst je rovnice ekvifázové plochy (vlnoplochy) a vektor grad L má směr kolmý na vlnoplochu, tedy směr šíření.

Vztah (2.3A.1) dosadíme do Maxwellových rovnic a za předpokladu, že vlnové číslo k je velké, dojdeme po dosti složitých úpravách k rovnici

{| g r a d L |}^{2} = n^{2}

( 2.3A.2 )

ve které

n = k / k_{0} = \sqrt{ε_{r e l} μ_{r e l}}

( 2.3A.3 )

je index lomu prostředí.

Rovnici (2.3A.2) budeme nazývat základní rovnicí geometrické optiky. Funkce L(x,y,z) je tzv. eikonála. Je to skalární funkce souřadnic. Vektor grad L má v každém bodě směr šíření vlny. Křivka, jejíž tečna má v každém bodě směr grad L, je paprsek. Paprsek má v každém bodě směr nejstrměji se měnící fáze a je to i směr Poyntingova vektoru, tedy směr toku energie. V nehomogenním prostředí mohou být paprsky zakřivené a rovnice (2.3A.2) je diferenciální rovnicí paprsků.

Pro praktické výpočty průběhu paprsků není tvar (2.3A.2) vhodný. Pro výpočet trajektorií paprsků se proto používají následující vztahy:

\frac{\partial}{\partial s} (n \frac{\partial x}{\partial s}) = \frac{\partial n}{\partial x}

\frac{\partial}{\partial s} (n \frac{\partial y}{\partial s}) = \frac{\partial n}{\partial y}

\frac{\partial}{\partial s} (n \frac{\partial z}{\partial s}) = \frac{\partial n}{\partial z}

( 2.3A.4 )

{(\frac{\partial x}{\partial s})}^{2} + {(\frac{\partial y}{\partial s})}^{2} + {(\frac{\partial z}{\partial s})}^{2} = 1

( 2.3A.5 )

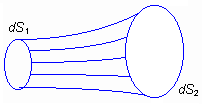
Proměnná s je křivočará souřadnice podél paprsku. Více k tomu je uvedeno ve vrstvě B včetně odvození a ilustrativního příkladu.

Geometrická optika umožňuje počítat nejen dráhy paprsků, ale i změny amplitudy a fáze intenzity pole podél paprsku. Postup je následující. Ve výchozím místě (např. A) zvolíme na vlnoploše (nekonečně) malou plošku dS₁ a každým bodem na okraji této plošky vedeme paprsek. Tak získáme paprskovou trubici. Na některé z následujících vlnoploch (B) má paprsková trubice jiný průřez dS₂ (obr. 2.3A.1). Protože energie se šíří podél paprsků, tak bočními stěnami z trubice nevystupuje. V bezeztrátovém prostředí jsou tedy výkony procházející ploškami dS₁ a dS₂ stejné. Jelikož P = Π S = (E²/Z₀) S a Z₀ = (μ/ε)^1/2, snadno odvodíme vztah mezi intenzitami na obou ploškách

\sqrt{\frac{ε_{1}}{μ_{1}}} {| E_{1} |}^{2} d S_{1} = \sqrt{\frac{ε_{2}}{μ_{2}}} {| E_{2} |}^{2} d S_{2}

( 2.3A.6 )

Fázi intenzity pole v místě B vypočítáme pomocí eikonály, konkrétně pomocí rovnic (2.3A.1), resp. (2.3A.2). Je-li na počátku uvažované dráhy (A) hodnota eikonály L_A, je v místě B (které musí být na tomtéž paprsku):

L_{B} = L_{A} + \int_{A}^{B} n d s

( 2.3A.7 )

Obr. 2.3A.1

Paprsková trubice

Integruje se podél paprsku.

Rovnice (2.3A.6) neplatí tam, kde se paprsky protínají (dostali bychom nekonečně velkou intenzitu pole). Taková situace nastává v ohnisku a na ploše zvané kaustika (viz poznámku ve vrstvě B).

Ve složitějších případech mají paprsky v různých příčných rovinách různé poloměry křivosti svých vlnoploch (jsou to např. astigmatické paprsky). V takových případech vztah (2.3A.6) také neplatí. Výpočet intenzity je však možný (viz vrstva B).