2.4 Geometrická teorie difrakce

Základní teorie

Geometrická optika je vhodnou metodou pro výpočty šíření vln v homogenních prostředích nebo v prostředích se spojitě proměnnými parametry. Selhává však v prostředích, v nichž jsou rozmístěna tělesa.

Obr. 2.4A.1 Ozářená odrážející polorovina z hlediska geometrické optiky

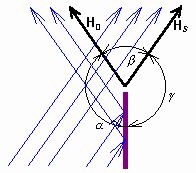
Všimněme si obrázku 2.4A.1. Tam je nakreslena situace v okolí ozářené odrážející poloroviny z pohledu geometrické optiky. Prostor v okolí poloroviny můžeme rozdělit na tři sektory: na sektor a , v němž se šíří jak dopadající tak i odražená vlna, na sektor b, kde je jen dopadající vlna, a na sektor g, v němž není (z pohledu geometrické optiky) žádná vlna. Sektory jsou od sebe přesně odděleny rovinami H₀ (hranice odrazu) a H_S (hranice stínu). Podle teorie geometrické optiky vzniká na těchto plochách nespojitost (skok) v průběhu intenzity pole, neboť na každé straně H₀ nebo H_S se počítá intenzita jinak. Ve skutečnosti je ovšem průběh intenzity spojitý a v oblasti stínu není intenzita nulová. V šedesátých letech 20. století navrhl Keller trochu svéráznou korekci geometrické optiky, aby odstranil nespojitosti pole v okolí těles. Tím dal základ k vytvoření tzv. geometrické teorie difrakce.

Geometrická teorie difrakce (GTD) je rozšířením geometrické optiky na nehomogenní prostředí. Řeší se interakce paprsků s tělesy a zákony geometrické optiky se doplní tak, aby se odstranily zjevné nesprávnosti (nespojitosti intenzit na hranici odrazu a stínu), ale aby se zachovaly hlavní přednosti GO (představa paprsků).

Původní rozpory geometrické optiky se odstraní těmito postuláty:

1. Paprsky dopadající vlny vybudí na ozářeném tělese nové vlny. Ty se šíří od tělesa, ne od původního zdroje. Jsou to tzv. difrakční vlny. Difrakční vlny lze také popisovat (počítat) pomocí paprsků. Difrakční vlny (difrakční paprsky) mají takové amplitudy a fáze, aby odstranily nespojitosti intenzit na rozhraních.
   Difrakční vlny se vybudí pouze těmi paprsky, které
   • dopadají na hrany tělesa, na ostří, na hranice různých poloměrů křivosti povrchu ap.
   • dotýkají se povrchu tělesa.
2. Amplituda difrakčních vln je úměrná amplitudě dopadající vlny. Konstanta úměrnosti se nazývá difrakční činitel.
3. Difrakční činitel je určen lokálními (!) vlastnostmi povrchu tělesa.

Tak např. na obr. 2.4A.2a jsou šipkami naznačeny paprsky difrakčních vln, vybuzených dopadem ozařující vlny na hranu poloroviny. Difrakční vlny tvoří soubor válcových vln, jejichž společným zdrojem je hrana poloroviny. V součtu s dopadající a odraženou vlnou zabezpečí spojité přechody intenzit na hranici odrazu i na hranici stínu a dají také nenulovou intenzitu za tělesem. Na obr. 2.4A.2b jsou nakresleny paprsky difrakčních vln vybuzených paprskem dopadající vlny, který se právě dotýká povrchu tělesa. Jakmile paprsek difrakční vlny opustí těleso, platí pro něj geometrická optika.

Velmi důležitý je poslední postulát o lokálních parametrech tělesa. V situaci na obr. 2.4A.2b je difrakční činitel určen pouze parametry e, m povrchu tělesa a poloměrem křivosti povrchu v místě, kde paprsek po povrchu klouže (je vyznačeno šrafovaně). Vůbec nezáleží na tom, jaký tvar a jaké vlastnosti má těleso někde dál. Díky tomu je možné řešit i složité difrakční situace, které se vyskytnou např. při šíření elektromagnetických vln v členitém terénu nebo ve městě (obr. 2.4A.2c).

a)	b)	c)
Obr. 2.4A.2 Geometrická teorie difrakce. Paprsky difrakčních vln a) na hraně poloroviny, b) na povrchu koule, c) na překážkách při šíření elektromagnetických vln terénem

Ale díky tomuto postulátu je možné také vypočítat hodnoty difrakčních činitelů. Tak např. pro všechna protáhlá tělesa, která mají na části svého povrchu stejný poloměr křivosti, platí stejný difrakční činitel. Ten musí být také stejný jako difrakční činitel pro (přesný) válec s týmž poloměrem. A difrakci na válci lze řešit exaktně. Jen je třeba výsledky exaktní teorie (takové, jaké jsme získali v čl. 2.2) upravit do tvaru, který je vhodný pro aplikaci v teorii geometrické optiky. To řeší tzv. kanonické problémy.

GTD společně s GO jsou účinnou metodou pro řešení difrakčních úloh. Předností je, že zůstává zachována představa paprsků, a že se pracuje s lokálními vlastnostmi povrchu tělesa. Pro aplikaci je bezpodmínečně nutný počítač a počáteční příprava je náročná.