2.4 Geometric theory of diffraction

Basic theory

Geometrical optics is a proper method for computing wave propagation in homogeneous media or in the environment exhibiting a continuous variation of parameters. If the environment contains objects, the method fails.

Fig. 2.4A.1 Illuminated reflecting half-plane from point of view of geometric optics

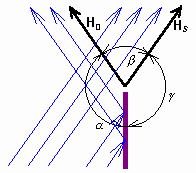
Look at the fig. 2.4A.1. We can observe the situation in the surrounding of an illuminated reflecting half-plane from the point of view of geometrical optics. The space around the half-plane can be subdivided into three sections: into the section a, where both the incident wave and the reflected one are present, into the section b, which contains the incident wave only, and to the section l, where no wave (from the point of view of geometrical optics) propagates. Moreover, exactly defined planes H₀ (border of reflection) and H_S (border of shade) separate the sections. From the point of view of geometrical optics, a discontinuity of the field distribution appears on those planes because on different sides of H₀ and H_S, intensity is computed in a different way. In real world, the field distribution is continuous, and in the section of shade, intensity is non-zero. In the sixties of 20^th century, Keller proposed a specific correction of geometrical optics in order to eliminate field discontinuities in the surrounding of objects. That way, the basics of the geometric theory of diffractionwere built.

Geometric theory of diffraction (GTD) is an extension of geometrical optics to inhomogeneous media. GTD solves interaction of beams and objects according to the laws of geometrical optics, which is completed that way to eliminate obvious incorrectness (intensity discontinuities at the border of the reflection section and the shade one) and to preserve the main advantages of geometrical optics (conception of beams). The incorrectness of geometric optics is eliminated following the below-described postulates:

1. Beams of the incident wave excite new waves on the illuminated object. Those waves propagate away from the object (not from the primary source). Those waves are called diffraction waves. Diffraction waves can be described (computed) using beams. Diffraction waves (diffraction beams are of such amplitudes and phases to eliminate field discontinuities on boundaries.
   Diffraction waves are excited only by the beams, which
   • "fall to the edges of the object, to the boundaries of different curvature radii of the surface, etc.
   • "touch the surface of the object.
2. Amplitude of diffraction waves is proportional to the amplitude of the incident wave. Proportionality coefficient is called diffraction factor.
3. Diffraction constant is given by local (!) properties of the object surface.

In fig. 2.4A.2a, arrows indicate diffraction waves excited by an incident wave illuminating the edge of the half-plane. Diffraction waves create the set of cylindrical waves, which common source is the half-plane edge. Adding incident and reflected wave together, continuous intensity transitions on the border of the reflection region and the shade one is ensured.

In fig. 2.4A.2b, beams of diffraction waves excited by the incident wave beam are depicted for the situation when the beam touches the object surface. In the moment when the beam of the diffraction wave leaves the object surface, it starts to behave according to the geometric optics rules.

Finally, the postulate about the local parameters of objects is very important. In the situation of fig. 2.4A.2b, the diffraction factor is given by parameters e, m of the object surface and by the curvature radius of the surface in the region, where the beam slides (over the surface. Parameters of the rest of the object do not play any role. Thanks to this property, even complicated diffraction situations appearing in a real terrain can be solved (fig. 2.4A.2c).

a)	b)	c)
Fig. 2.4A.2 Geometric theory of diffraction. Diffraction waves beams a) on the half-plane edge, b) on the spherical surface, c) on obstacles in the real terrain

Thanks to the above-mentioned postulate, values of diffraction factors can be computed. E.g., all the oblong objects, which have the same curvature radius of a certain part of their surface, have the same diffraction factor. The factor has to be the same as for the cylinder of the same radius. And the diffraction on a cylinder can be solved exactly. We only have to rearrange the results of the exact theory (see the chapter 2.2) to the form applicable to the theory of geometric optics. This is solved by so called canonical problems.

GTD is together with geometrical optics an efficient tool for solving diffraction problems. Preserving the conception of beams and computing with local object properties are the main advantages of the method. The method has to be implemented using computer.