2.5 Šíření vln ve vrstevnatém prostředí

Základní teorie

V některých technických zařízeních se využívají prostředí, složená z několika těsně k sobě přiléhajících vrstev, lišících se permitivitou (případně permeabilitou) a také svou tloušťkou. Rozhraní mezi nimi jsou obvykle rovinná a navzájem rovnoběžná. Vrstevnaté prostředí je tedy složeno z určitého počtu planparalelních dielektrických vrstev (případně desek).

Vrstevnatá prostředí (hovoří se také o vrstevnatých strukturách) umožňují realizovat např. bezodrazové plochy (stěny). Vlna, dopadající na plochu pokrytou několika dielektrickými vrstvami se správně zvolenými parametry, se ve vrstvách pohltí, aniž by se větší mírou odrážela zpět (činitel odrazu je blízký nule). S aplikacemi se setkáme např. v bezodrazových komorách, na měřicích pracovištích a také u některých vojenských prostředků.

Vrstevnaté struktury mohou také zajistit bezodrazový přechod vlnění z jednoho prostředí do prostředí jiného (např. ze vzduchu do vody) ve smyslu impedančního přizpůsobení. Přizpůsobovacím obvodem je v tomto případě soubor několika dielektrických vrstev vložených mezi obě prostředí. Do této skupiny patří i dielektrické kryty antén a jiných vysokofrekvenčních zařízení. Kryt musí příslušný objekt mechanicky chránit, ale pro elektromagnetické vlny se musí chovat tak, jakoby tam nebyl.

Další aplikační oblastí vrstevnatých prostředí jsou kmitočtové filtry. Ty propouštějí (nebo nepropouštějí) elektromagnetické vlnění jen v určitém kmitočtovém pásmu. Filtrem je opět blok několika dielektrických vrstev. Filtry tohoto typu se používají častěji v optice, ale setkáme se s nimi i na rádiových kmitočtech.

V dalším výkladu se omezíme na případy, kdy vlnění dopadá na rozhraní mezi vrstvami kolmo. Výklad rozdělíme do dvou částí. V prvé části (vrstva A) budeme sledovat, co se děje uvnitř prostředí, jak se mění intenzity polí na jednotlivých rozhraních a v jednotlivých dielektrických vrstvách. V druhé části (vrstva B) bude náš pohled spíše globální a stanovíme parametry prostředí jako celku.

Ve vrstevnatém prostředí dochází k vícenásobnému odrazu a vniku vlnění na jednotlivých rozhraních. Proto si nejprve připomeneme důležité pojmy týkající se odrazu a vniku.

kolmá polarizace

rovnoběžná polarizace

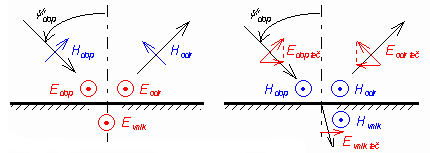
Obr. 2.5A.1

Tečné složky výsledné intenzity po obou stranách rozhraní jsou stejné. Z grafických důvodů jsou vektory nakresleny mimo rozhraní.

Rovina rozhraní je rovina, oddělující dvě prostředí. Rovina dopadu je určena těmito podmínkami: je kolmá na rovinu rozhraní a je rovnoběžná se směrem šíření vlny. Vlna kolmo polarizovaná má vektor E kolmý na rovinu dopadu. Vlna rovnoběžně polarizovaná má vektor E rovnoběžný s rovinou dopadu. Orientace vektorů pro obě polarizace je nakreslena na obr. 2.5A.1. Rovina rozhraní je kolmá k nákresně a je vyznačena šrafováním. Rovina dopadu je rovina nákresny.

Každý bod roviny rozhraní musíme považovat za dva body nekonečně blízké. Jeden leží v jednom prostředí, druhý v druhém. V každém místě roviny rozhraní jsou proto dvě různé intenzity pole E₁, E₂ a H₁, H₂ - každá je v jiném prostředí. Vždy však musí platit rovnost tečných složek intenzit elektrického pole a rovnost normálových složek dielektrického posuvu:

E_{1 t e č} = E_{2 t e č}

ε_{1} E_{1 n o r m} = ε_{2} E_{2 n o r m}

(na rovině rozhraní)

( 2.5A.1 )

Analogické vztahy platí i pro vektory H, pokud na rozhraní netečou proudy. Ze základní okrajové podmínky (2.5A.1) vyplývají bezprostředně důležité vztahy mezi intenzitami, označenými v obr. 2.5A.1:
při kolmé polarizaci:

E_{v n i k} = E_{d o p} + E_{o d r} = E_{d o p} (1 + ρ_{⊥})

( 2.5A.2a )

při rovnoběžné:

E_{v n i k} \cos ψ_{v n i k} = E_{d o p} \cos ψ_{d o p} - E_{o d r} \cos ψ_{o d r} = E_{d o p} (1 - ρ_{∥}) \cos ψ_{d o p}

;

( 2.5A.2b )

ρ_⊥ a ρ_|| jsou činitele odrazu pro kolmo a rovnoběžně polarizovanou vlnu.

Obecně

ρ = \frac{E_{o d r}}{E_{d o p}}

Jak jsme již uvedli, budeme se zabývat pouze případy, kdy vlnění dopadá na rozhraní mezi vrstvami kolmo. Činitele odrazu pak závisejí pouze na vlnových impedancích Z₀₁ a Z₀₂ obou prostředí

ρ_{⊥} = \frac{Z_{02} - Z_{01}}{Z_{02} + Z_{01}}

ρ_{∥} = \frac{Z_{01} - Z_{02}}{Z_{01} + Z_{02}} = - ρ_{⊥}

( 2.5A.3 )

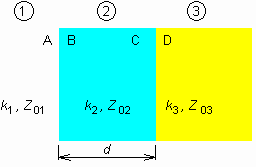
Obr. 2.5A.2

Vrstevnaté prostředí

Při kolmém dopadu mizí rozdíl mezi polarizacemi. Činitelé odrazu se sice liší znaménkem, ale kladný směr E_odr se zase liší orientací (viz obr. 2.5A.1), takže výsledek je pro obě polarizace stejný.

Po tomto úvodu můžeme přistoupit k vlastnímu výkladu. Při šíření ve vrstevnatém prostředí se mnohokrát opakuje stejný děj: vlnění přechází přes rozhraní a pak se volně šíří dielektrickou vrstvou k dalšímu rozhraní. Stačí tedy fyzikálně a matematicky zvládnout ony dva jevy: přechod přes rozhraní a šíření vrstvou.

K výkladu použijeme obrázek 2.5A.2, na němž máme 3 prostředí 1 až 3 (tedy o jedno více než nutně k výkladu potřebujeme). Shodně jsou indexovány i jejich vlnové impedance Z_0i = (μ_i / ε_i)^1/2 a vlnová čísla v nich k_i = ω (μ_iε_i)^1/2. Prostředí jsou oddělena dvěma rozhraními, z nichž každé má dvě plochy (A, B; C, D): jedna leží v jednom prostředí, druhá plocha v druhém prostředí. Vlnění přichází zleva, prochází přes rozhraní kolmo, a jak jsme již uvedli, je kolmo polarizované; vektory E a H jsou tečné k rozhraní. V obecném případě se šíří ve všech prostředích vlna přímá i vlna zpětná (odražená) a je tam tudíž stojaté vlnění. Intenzity (E i H) přímé vlny označíme indexem p, intenzity zpětné vlny indexem z. Další index udává, ve kterém místě, resp. na které ploše (A, B, C, D) příslušná intenzita je. Výsledné intenzity označíme jen písmenem (bez indexu p nebo z)

E = E^{(p)} + E^{(z)}

H = H^{(p)} - H^{(z)}

( 2.5A.4 )

(záporné znaménko v rovnici (2.5A.4b) vyplývá z obr. 2.5A.1). Podle uvedeného je tedy např. E_B je výsledná intenzita na rozhraní 1-2, ale v prostředí 2, E_A^(z) je intenzita odražené vlny na tomtéž rozhraní, ale v prostředí 1.

Analýzu poměrů ve vrstevnatém prostředí je možné vést dvojím způsobem. Rozdíl je sice jen formální, ale v jednotlivých situacích může hrát určitou roli z hlediska techniky výpočtu. Ať použijeme kterýkoli způsob, je výhodné (a často nutné) postupovat od konce prostředí k jeho počátku (proti směru šíření přímé vlny).

První způsob vychází bezprostředně z okrajové podmínky (2.5A.1). Výsledné intenzity na obou stranách rozhraní musí být stejné. Tedy např. pro rozhraní 2-3 je:

E_{C}^{(p)} + E_{C}^{(z)} = E_{D}^{(p)} + E_{D}^{(z)}

( 2.5A.5a )

H_{C}^{(p)} - H_{C}^{(z)} = H_{D}^{(p)} - H_{D}^{(z)}

( 2.5A.5b )

V druhé rovnici vyloučíme H dosazením H^(p) = E^(p) / Z₀, H^(z) = E^(z) / Z₀ a získáme dvě rovnice pro E_C^(p) a E_C^(z), když veličiny ve třetím prostředí považujeme za známé (postupujeme od konce). Z těchto rovnic nalezneme:

E_{C}^{(p)} = \frac{1}{2} [E_{D}^{(p)} (1 + \frac{Z_{02}}{Z_{03}}) + E_{D}^{(z)} (1 - \frac{Z_{02}}{Z_{03}})] = \frac{1}{2} [(E_{D}^{(p)} + E_{D}^{(z)}) + (E_{D}^{(p)} - E_{D}^{(z)}) \frac{Z_{02}}{Z_{03}}]

( 2.5A.6a )

E_{C}^{(z)} = \frac{1}{2} [E_{D}^{(p)} (1 - \frac{Z_{02}}{Z_{03}}) + E_{D}^{(z)} (1 + \frac{Z_{02}}{Z_{03}})] = \frac{1}{2} [(E_{D}^{(p)} + E_{D}^{(z)}) - (E_{D}^{(p)} - E_{D}^{(z)}) \frac{Z_{02}}{Z_{03}}]

( 2.5A.6b )

Tím je vyřešen přechod přes rozhraní. Pro šíření vlny ve vrstvě platí dobře známé vztahy

E_{B}^{(p)} = E_{C}^{(p)} \exp (+ j k_{2} d)

( 2.5A.7a )

E_{B}^{(z)} = E_{C}^{(z)} \exp (- j k_{2} d)

( 2.5A.7b )

v nichž d je tloušťka vrstvy. (v první rovnici se postupuje proti směru šíření vlny, a proto je kladné znaménko v exponentu; v druhé rovnici je tomu naopak). Intenzity E₂^(p) a E₂^(z) jsou vstupními veličinami pro předchozí rozhraní 1-2. Při analýze šíření ve vrstevnatém prostředí se tedy opakovaně aplikují rovnice (2.5A.6) a (2.5A.7) po patřičné záměně indexů.

Kdekoli uprostřed vrstvy můžeme vypočítat výsledné intenzity polí tak, že do rovnic (2.5A.7) dosadíme souřadnici požadovaného místa místo tloušťky d a pak použijeme vzorce (2.5A.4). Pro činitele odrazu a poměr stojatých vln (ve kterémkoli místě) platí známé vzorce:

ρ = \frac{E^{(z)}}{E^{(p)}}

P S V = \frac{1 + ρ}{1 - ρ}

( 2.5A.8 )

Vnucuje se otázka, proč máme (a většinou musíme) postupovat od konce vrstevnaté struktury k jejímu počátku, když bude předem známa spíše intenzita pole na počátku než na konci. Důvod je ve fyzikální podstatě věci. Poměry kdekoli v prostředí jsou závislé na tom, co je na jeho konci. Rovnice (2.5A.6) a (2.5A.7) sice formálně připouštějí postup od počátku ke konci, ale ve skutečné situaci, když budeme znát třeba výslednou intenzitu pole na počátku, tak předem nevíme, jak ji rozložit na intenzitu přímé vlny a intenzitu odražené vlny. A právě obě tyto intenzity vstupují do rovnic (2.5A.6) a (2.5A.7). Naproti tomu na konci prostředí je situace jiná. Pomineme-li zcela výjimečné případy, může být na konci prostředí buď volný prostor anebo dokonale vodivá stěna (kdyby tam bylo něco jiného, tak to ještě není konec prostředí). Je-li na konci volný prostor, tak tam odražená vlna neexistuje (E^(z) = 0) a pro výpočet stačí znát jedinou intenzitu E^(p). Je-li prostředí akončeno vodivou stěnou, víme předem, že E^(z) = - E^(p), a tedy rovněž stačí znát jedinou intenzitu. Tuto intenzitu zvolíme např. jednotkovou a počítáme směrem dopředu, až dojdeme k některé předem známé (zadané) intenzitě. Pak v poměru zadané intenzity a námi vypočtené hodnoty přepočítáme všechny předchozí výsledky; všechny použité vztahy jsou totiž lineární.

Jiný způsob řešení poměrů ve vrstevnaté struktuře využívá transformace činitele odrazu. Jde o stejný postup, který se používá v teorii vedení při řešení poměrů na soustavě vedení, spojených v kaskádě (za sebou). V obou případech jde totiž o stejnou situaci: máme několik úseků (prostředí) řazených za sebou v kaskádě a každé má svou charakteristickou (vlnovou) impedanci Z₀ a svou délku (tloušťku) d. Napětí a proudu na vedení odpovídají intenzity E a H v dielektrickém prostředí.

Postup řešení je následující. Vypočteme činitele odrazu na posledním rozhraní v předposledním prostředí (viz obr. 2.5A.2):

ρ_{C} = \frac{Z_{03} - Z_{02}}{Z_{03} + Z_{02}}

( 2.5A.9 )

Činitele odrazu přepočítáme na počátek předposledního prostředí, na plochu B:

ρ_{B} = ρ_{C} \exp (- 2 j k d)

( 2.5A.10 )

Abychom nalezli činitele odrazu na ploše A, musíme nejprve vypočítat impedanci na ploše B

Z_{B} = Z_{02} \frac{1 + ρ_{B}}{1 - ρ_{B}}

( 2.5A.11 )

a z ní teprve činitele odrazu na A:

ρ_{A} = \frac{Z_{B} - Z_{01}}{Z_{B} + Z_{01}}

( 2.5A.12 )

Má-li struktura více vrstev, pak se uvedené výpočty jen opakují po potřebné záměně indexů.

Tato část řešení musí opět probíhat směrem od konce struktury k počátku. Výpočty intenzit polí pak mohou proběhnout v libovolném směru od známé (zadané) intenzity k ostatním. Je-li známa např. výsledná intenzita elektrického pole E_A na ploše A, rozložíme ji nejprve na intenzity přímé a zpětné vlny. Protože

E_{A}^{(p)} + E_{A}^{(z)} = E_{A}^{(p)} + ρ_{A} E_{A}^{(p)} = E_{A}

E_{A}^{(p)} = \frac{E_{A}}{1 + ρ_{A}}

E_{A}^{(z)} = E_{A}^{(p)} ρ_{A}

( 2.5A.13 )

Stejný rozklad můžeme provést ve kterémkoli prostředí (vrstvě) po patřičné změně indexů. Pro výpočet intenzit polí uvnitř struktury využijeme okrajovou podmínku (2.5A.1) a rozklad (2.5A.13). Například

E_{B} = E_{A}

E_{B}^{(p)} = \frac{E_{B}}{(1 + ρ_{B})}

E_{B}^{(z)} = E_{B}^{(p)} ρ_{B}

Pomocí rovnic (2.5A.7) vypočteme E_C^(p) a E_C^(z), pak výslednou E_C, atd. K výpočtu intenzit je možné po malé úpravě použít také rovnic (2.5A.5) resp. (2.5A.6).

Další způsob analýzy šíření vln ve vrstevnatém prostředí je popsán ve vrstvě B. Tam jsou uvedeny i některé podrobnější informace k aplikacím vrstevnatých struktur.