2.5 Šíření vln ve vrstevnatém prostředíPodrobnější popisVe vrstvě A jsme si ukázali dva postupy, umožňující řešit šíření elektromagnetického vlnění vrstevnatým prostředím. První postup vycházel z rozložení intenzit polí a ze základní okrajové podmínky, druhý postup využíval transformace činitele odrazu a byl v podstatě totožný s běžně užívaným postupem při řešení obdobných úloh na vedení. Zde uvedeme ještě jeden postup, který celé řešení více formalizuje a proto je vhodný zvláště pro složitější situace.
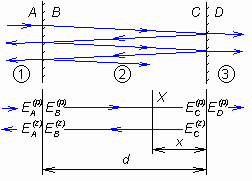
Pro základní výklad zvolíme opět jen tři prostředí (dvě rozhraní), stejně jak jsme to učinili již ve vrstvě A. Situace nakreslena na obr. 2.5B.1. Není obtížné si představit, že ve vrstevnatém prostředí dochází k mnohonásobným odrazům a v každé vrstvě existuje nekonečný počet vln šířících se jedním i druhým směrem. Všechny vlny jsou však koherentní a víme, že koherentní vlny šířící se stejným směrem lze vždy sečíst a výsledkem je jediná harmonická vlna. Proto stačí, abychom i v naší úloze uvažovali v každém prostředí jen dvě vlny, jak je nakresleno na obr. 2.5B.1 dole (i toto jsme již mlčky uvažovali při výkladu ve vrstvě A). Jednotlivá prostředí označíme 1, 2, 3, a dále A je povrch rozhraní 1-2 ležící v prostředí 1, B je povrch rozhraní 1-2 v prostředí 2, atd. Pomocí indexů A, B, C, D označíme povrch, na kterém intenzitu pole počítáme a závorkovanými exponenty (p), (z) označíme směr šíření (přímá vlna, zpětná vlna). Tak např. EB(z) je intenzita zpětné (odražené) vlny na ploše B, tj. na rozhraní 1-2 v prostředí 2. Vrstevnaté prostředí jsou střídavě naskládaná rozhraní a vrstvy; vyšetříme samostatně přechod vlnění přes rozhraní a jeho přechod vrstvou. Uvážíme rozhraní 1-2 a vyjádříme intenzity vln, které se od tohoto rozhraní rozbíhají. Odražená vlna s intenzitou EA(z) vzniká jednak odrazem dopadající vlny s intenzitou EA(p), jednak prostupem vlny EB(z) z prostředí 2 do prostředí 1. Podobně vlna s intenzitou EB(p) vzniká jednak prostupem vlny EA(p) z prostředí 1 do prostředí 2, jednak odrazem vlny s intenzitou EB(z). Platí tedy rovnice:
kde ρ12 je činitel odrazu vlny šířící se prostředím 1 a odrážející se od rozhraní s prostředím 2 a ρ21 je činitel odrazu vlny šířící se prostředím 2 a odrážející se od rozhraní s prostředím 1. Analogicky jsou indexovány činitele vniku (prostupu) τ12 a τ21. Rovnice (2.5B.1) přepíšeme do maticového tvaru:
Matice na pravé straně, která je složená z činitelů odrazu a vniku, je rozptylová matice rozhraní. Jak je vidět, rozptylová matice se celkem snadno sestaví, a navíc její prvky mají zřejmý a jednoduchý fyzikální význam (jsou to činitelé odrazu a vniku). Pro řešení naší úlohy však rovnice (2.5B.2) vhodná není, protože ve vstupní a výstupní sloupcové matici jsou intenzity vstupního a výstupního vlnění prostřídány. Rovnici (2.5B.2) proto vyřešíme pro EA(p) a EA(z). Při úpravě vezmeme v úvahu, že ρ21 = -ρ12 a τ12 τ21 - ρ12 ρ21 = 1. Výsledek zapíšeme hned v maticovém tvaru:
Matice na pravé straně je kaskádní maticí rozhraní. Sloupcová matice na levé straně obsahuje intenzity vstupního vlnění, sloupcová matice na pravé straně pak intenzity výstupního vlnění. Kaskádní matice je vhodná právě pro kaskádní řazení prvků (dvojbranů), které máme i v naší úloze. Při kaskádním řazení libovolného počtu prvků stačí jen násobit jejich kaskádní matice. Nyní musíme ještě odvodit kaskádní matici dielektrické vrstvy. To se nám podaří přímo (bez nutnosti sestavovat rozptylovou matici). V dielektrické vrstvě jsou dvě proti sobě se šířící postupné vlny. Zřejmě platí EB(z) = EC(z) exp(-jk2d), EB(p) = EC(p) exp(+jk2d). Tudíž
kde k2 je vlnové číslo v druhém prostředí. V soustavě planparalelních vrstev jde o kaskádní řazení jednotlivých rozhraní a vrstev. Výslednou rovnici sestavíme ze součinů příslušných matic. Pro situaci na obr. 2.5B.1:
Ve výsledku předpokládáme, že ve třetím prostředí je jen postupná vlna. Kdyby tomu tak nebylo, objeví se v poslední sloupcové matici intenzita ED(z). Možnost rozšíření úvahy na libovolný počet vrstev je zřejmá. Rozepsáním (2.5B.5) dostaneme:
Poměr EA(z) / EA(p) udává skutečnou hodnotu činitele odrazu na rozhraní 1-2. Poměr intenzit polí ED(p) / EA(p) je celkový činitel prostupu. Obě veličiny lze vypočítat z posledních rovnic. Připomeňme ještě, že při kolmém dopadu kolmo polarizované vlny na jediné rozhraní (za ním nesmí existovat odražená vlna!) platí pro činitele odrazu a prostupu následující vztahy:
Uvedená metoda řešení poměrů ve vrstevnatých prostředích je výhodná ve složitějších případech. Běžné úlohy lze řešit numericky pomocí Smithova diagramu nebo přímo z okrajové podmínky na rozhraní, jak bylo popsáno ve vrstvě A. Jak jsme uvedli v úvodních odstavcích této kapitoly, jednou z praktických aplikací vrstevnatých struktur je zabezpečení bezodrazového přechodu elektromagnetického vlnění z jednoho prostředí do jiného. Takový požadavek se může vyskytnout např. při buzení vln v zemi nebo jiných materiálech (elektromagnetický průzkum, defektoskopie), při buzení vln v tělní tkáni anebo u dielektrických krytů antén, kdy vlna musí do dielektrika vstoupit a pak opět vystoupit pokud možno se stejnou intenzitou a ekvifázovou plochou. Požadavek lze více či méně úspěšně řešit tím, že rozhraní mezi oběma prostředími se pokryje jednou nebo několika dielektrickými vrstvami s přesně stanovenými permitivitami a tloušťkami. Tyto vrstvy plní funkci přizpůsobovacího obvodu (transformátoru) stejně, jako je tomu u přizpůsobovacích obvodů na vedení. V obou případech se strukturou šíří elektromagnetické vlnění. Na vedení je charakterizované napětím a proudem, v dielektrické vrstvě intenzitou elektrického a magnetického pole. Vzájemně si odpovídají U a E, a pak I a H. Charakteristická impedance vedení odpovídá vlnové impedanci prostředí (vrstvy). Rozdíl mezi oběma případy je ve struktuře obvodů. Na vedení bylo možné tvořit přizpůsobovací obvody vkládáním úseků vedení a také připojováním paralelních či sériových reaktancí. Přizpůsobovací vrstvy lze řadit pouze za sebou (do kaskády), nikoli paralelně nebo sériově. Důvod je principiální. Např. na vedení v místě, kde je připojená paralelní reaktance, vzniká skok proudu; část proudu totiž protéká onou reaktancí. U vrstevnatého ekvivalentu by musel v příslušném místě (na rozhraní) existovat skok v intenzitě magnetického pole. To není na prostém rozhraní fyzikálně možné, odporuje to základní okrajové podmínce. Obecně ovšem skok v intenzitě H na rozhraní možný je, pokud připustíme, aby po rozhraní tekl elektrický proud. Okrajová podmínka má v takovém případě tvar n × H1 = K + n × H2. Indexy je rozlišeno jedno a druhé prostředí, vektorové součiny s normálou n dávají tečné složky a K [A m-1] je povrchová hustota elektrického proudu na rozhraní. V praxi se používají konstrukce využívající této možnosti. Jejich technologické řešení musí ovšem umožňovat tok elektrických proudů po ploše rozhraní. Běžně lze navrhovat a konstruovat přizpůsobovací obvody složené z jedné čtvrtvlnné dielektrické vrstvy (čtvrtvlnný transformátor) nebo z jedné vložené vrstvy určité délky a druhé vrstvy čtvrtvlnné. Je jedno, zda se jedná o úseky vedení nebo o dielektrické vrstvy. Pokud je to účelné, je možné použít Smithův diagram. Pro demonstraci působení takovýchto přizpůsobovacích obvodů a pro ilustraci jejich vlastností je ve vrstvě C prezentován matlabovský program. Program není určen pro výpočet (návrh) těchto obvodů, ale pro obvod se známými parametry (permitivity a tloušťky vrstev) vypočítá rozložení E a H v jednotlivých vrstvách a činitele odrazu a poměry stojatých vln v různých místech přizpůsobovací struktury. Je tedy možné na číselných hodnotách sledovat, jak obvod vlastně pracuje. Lze programovat struktury složené až ze čtyř dielektrických vrstev (např. kaskádní transformátor). Lze také sledovat, jak se obvod chová v širším (i poměrně velmi širokém) kmitočtovém pásmu. Jinou aplikační oblastí vrstevnatých struktur jsou kmitočtové filtry. Základním prvkem těchto filtrů je půlvlnná dielektrická vrstva. Ta, stejně jako půlvlnné vedení, transformuje intenzity i impedance v poměru 1:1. Chová se tedy tak, jakoby tam nebyla. Jinak řečeno, vlnění odražené na začátku vrstvy se právě ruší s vlněním, odraženým na konci vrstvy. Jestliže však přichází vlnění s odlišným kmitočtem (pro který již vrstva není přesně půlvlnná), pak už k úplnému zrušení odražených vln nedochází. Vrstva jako celek odráží část energie a o tuto část je ochuzeno vlnění, které vrstvou prochází. Procházející vlnění je zeslabeno, za vrstvou má menší intenzitu než před ní. Před rozladěnou vrstvou se ovšem objeví stojaté vlnění. Prakticky použitelné filtry vznikají kombinací několika půlvlnných vrstev oddělených vzájemně vrstvami s jinou permitivitou a jinou délkou (např. λ/4). Protože vlastnosti půlvlnné vrstvy se opakují na dvoj-, troj- a vícenásobném kmitočtu (tloušťka vrstvy λ, 3λ/2 atd.), opakují se i vlastnosti těchto filtrů na násobcích základního kmitočtu. Jsou to filtry hřebenové. Vlastnosti vrstevnatých struktur jako filtrů lze demonstrovat dalším programem ve vrstvě C. Tam je i podrobnější popis tohoto programu. |