3.1 Vlnovody

Základní teorie

Vrstva A tohoto článku přináší základní informace o šíření elektromagnetického vlnění ve vlnovodu. Ve vrstvě B pak uvádíme anglický překlad vrstvy A. Chceme tím čtenáři pomoci seznámit se s anglickou terminologií z oblasti vlnovodů a mikrovlnných vedení.

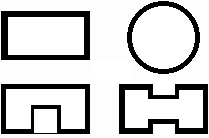
Obr. 3.1A.1

Vlnovody

Druhy vedení, které známe z každodenního života (koaxiální vedení, dvojlinka), jsou jen omezeně použitelné v mikrovlnných kmitočtových pásmech, protože s růstem kmitočtu přenášeného signálu významně rostou ztráty v dielektriku těchto vedení. Proto se na vyšších kmitočtech používají pro přenos signálu velmi často vlnovody.

Termínem vlnovod většinou označujeme kovovou trubici, jejíž příčné rozměry jsou srovnatelné s délkou vlny. Vnitřní stěny vlnovodu bývají upraveny tak, aby byly minimalizovány ztráty v kovu (obvykle lze stěny vlnovodu pokládat za dokonalý elektrický vodič). Příčný profil vlnovodu má obvykle obdélníkový nebo kruhový tvar. Ve speciálních případech může mít průřez vlnovodu tvar písmene Π nebo H (obr. 3.1A.1); tyto vlnovody jsou širokopásmovější než běžný obdélníkový vlnovod, avšak na druhou stranu přenášejí menší výkon.

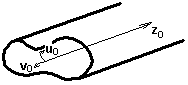
Obr. 3.1A.2

Podélně homogenní vlnovod. u,v: příčné směry, z: podélný směr.

S vlnovody se setkáváme na kmitočtech řádu gigahertzů, protože na nižších kmitočtech by měly příliš velké příčné rozměry. Vlnovody nacházíme zejména u radiolokátorů a u systémů pro družicovou komunikaci. Slouží zde jednak pro přenos energie z vysokofrekvenčního generátoru k anténě, jednak pro přenos signálu z antény k vysokofrekvenčnímu stupni přijímače.

Předpokládejme, že máme k dispozici podélně homogenní kovový vlnovod libovolného průřezu (obr. 3.1A.2). Zajímá nás, jaké se v něm vybudí pole, vsuneme-li do něj sondu, protékanou vysokofrekvenční proudem.

Předpokládáme-li, že jsme hodně vzdáleni od zdroje pole, tj. od místa buzení vlnovodu, můžeme vyjít z homogenních vlnových rovnic pro podélnou složku elektrického a magnetického Hertzova vektoru Π_z^e a Π_z^m. Jelikož rozložení pole v podélném směru z je nezávislé na rozložení pole v příčných směrech u a v, lze každý Hertzův vektor rozepsat jako součin dvou funkcí, z nichž jedna je závislá pouze na příčných souřadnicích u, v a druhá jen na souřadnici podélné z, tj. Π_z = T₁(u,v) × T₂(z). Metodou separace proměnných dospějeme k separačním konstantám Γ a γ, které jsou svázány vzájemně vztahem

γ^{2} + k^{2} = Γ^{2}

( 3.1A.1 )

V tomto vztahu je Γ separační konstanta svázaná s rozložením elektromagnetického pole v příčných směrech vlnovodu, γ je konstanta svázána s šířením vlnění v podélném směru vlnovodu a k je vlnové číslo prostředí ve vlnovodu (vakuum s permitivitou ε₀ a permeabilitou μ₀)

k = ω \sqrt{μ_{0} ε_{0}}

( 3.1A.2 )

a ω je úhlový kmitočet vlny.

Podrobnější matematický popis uvedeného postupu nalezneme v [1].

Řešením rovnice pro šíření elektromagnetického vlnění v podélném směru vlnovodu dospějeme ke vztahu

T_{2} = C_{1} e^{γ z} + C_{2} e^{- γ z}

( 3.1A.3 )

C₁ a C₂ jsou integrační konstanty. První sčítanec popisuje zpětnou vlnu (šíří se proti směru osy z), druhý sčítanec vlnu přímou (šíří se ve směru z). Separační konstantu γ nazýváme součinitelem přenosu (konstantou šíření) a rozepisujeme ji jako

γ = β + j α

( 3.1A.4 )

Z (3.1A.3) je zřejmé, že β má význam měrného útlumu a α je měrná fáze (fázová konstanta).

Jelikož vlnové číslo k je reálné (ve vlnovodu uvažujeme bezeztrátové prostředí) a jelikož separační konstanta Γ je reálná také (jak ukážeme za chvíli), může součinitel přenosu nabývat následujících hodnot:

γ = β pro k < Γ v podélném směru se bude šířit tzv. evanescentní vlna;
γ = α pro k > Γ v podélném směru se šíří netlumená vlna;
γ = jk pro Γ = 0 nezáleží na průřezu vlnovodné struktury (viz dvouvodičová vedení).

Protože vlnové číslo je přímo úměrné kmitočtu vlny, můžeme z prvních dvou výše uvedených bodů vyvodit zajímavý závěr: Zatímco vlny, jejichž kmitočet je nižší nežli

ω_{k r i t} = Γ / \sqrt{μ ε}

( 3.1A.5 )

se vlnovodem vůbec nešíří, vlny o kmitočtu vyšším nežli ω_krit se stejným vlnovodem budou šířit bez útlumu. Onen význačný kmitočet (3.1A.5) je nazýván kmitočtem kritickým.

Obr. 3.1A.3

Závislost fázové a skupinové rychlosti na kmitočtu.

Věnujme se nyní jevům, které se objeví na nadkritických kmitočtech f > f_krit. Ze vztahu (3.1A.1) dostaneme po dosazení za γ = jα výraz

α = \sqrt{k^{2} - Γ^{2}}

( 3.1A.6 )

Vyjádříme-li separační konstantu Γ ze vztahu (3.1A.5)

Γ = ω_{k r i t} \sqrt{μ ε}

a vezmeme-li vlnové číslo k ze vztahu (3.1A.2) po jednoduché úpravě dospějeme ke vztahu pro fázovou konstantu v podélném směru

α = k \sqrt{1 - {(f_{k r i t} / f)}^{2}}

( 3.1A.7 )

Dosadíme-li fázovou konstantu (3.1A.7) do vztahu pro fázovou rychlost

v_{f} = ω / α

dostáváme závislost fázové rychlosti ve vlnovodu na kmitočtu

v_{f} = \frac{v}{\sqrt{1 - {(f_{k r i t} / f)}^{2}}}

( 3.1A.8 )

Symbol v ve vztahu (3.1A.8) značí fázovou rychlost naší vlny z vlnovodu ve volném prostoru, který by měl stejné parametry jako obsah vlnovodu (v našem případě vakuum)

v = 1 / \sqrt{μ ε}

( 3.1A.9 )

Obr. 3.1A.4

Disperze vln

Ze známé fázové rychlosti odvodíme dosazením do vztahu mezi délkou vlny a fázovou rychlostí

λ_{g} = v_{f} / f

( 3.1A.10 )

vztah pro délku vlny ve vlnovodu v podélném směru

λ_{g} = \frac{λ}{\sqrt{1 - {(f_{k r i t} / f)}^{2}}}

( 3.1A.11 )

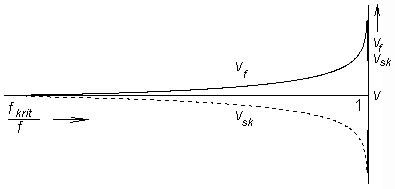
kde λ značí délku naší vlny ve volném prostoru, jehož parametry odpovídají parametrům prostředí uvnitř vlnovodu.

Pokud se zajímáme o rychlost šíření energie vlnovodem (a nikoli o rychlost šíření fáze), musíme vypočíst skupinovou rychlost. Jelikož součin skupinové rychlosti a rychlosti fázové musí být roven kvadrátu rychlosti světla, pro skupinovou rychlost dostáváme vztah

v_{s k} = v \sqrt{1 - {(f_{k r i t} / f)}^{2}}

( 3.1A.12 )

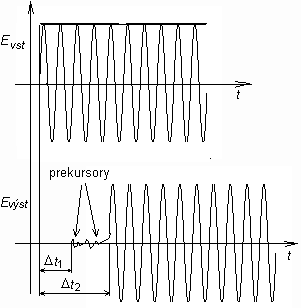
kde v je opět fázová rychlost ve volném prostoru.

Dosud jsme předpokládali, že se vlnovodem šíří harmonická vlna. Co se však bude dít při přenosu vlny, složené z několika kmitočtů? Z výše uvedeného je zřejmé, že každá frekvenční složka se bude šířit jinou rychlostí, takže výstupní signál bude odlišný od signálu vstupního, bude zkreslený. Říkáme, že dochází k disperzi vln (obr. 3.1A.4).

Prozatím jsme se zabývali analýzou rozložení pole v podélném směru. Výsledky této analýzy nezávisejí na příčném průřezu, a tudíž platí pro jakýkoli homogenní vlnovod. Pro příčné směry vlnovodu je situace zcela opačná:

V příčném směru se nešíří vlnění (nemá kam se šířit). V těchto směrech se vzájemně sčítají vlny odražené od stěn vlnovodu, takže zde vzniká stojaté vlnění.
Jelikož odrazy od stěn (a tedy i charakter stojatého vlnění) závisejí na profilu vlnovodu, je zapotřebí analýzu pole v příčných směrech provádět vždy pro specifický tvar profilu. V našem výkladu se omezíme na profil obdélníkový.

Analýzu vykonáme pro dva typy vln, které se mohou vlnovodem šířit. Jedná se o vlny příčně magnetické (TM), u nichž má vektor magnetické intenzity nenulové složky pouze v příčném směru, a o vlny příčně elektrické (TE), u nichž má vektor intenzity elektrického pole nenulové složky jen ve směru příčném. Postupem uvedeným v [1] bychom dospěli pro oba typy vln k následujícímu vztahu pro kritický úhlový kmitočet:

ω_{k r i t} = \frac{1}{\sqrt{μ ε}} \sqrt{{(\frac{m π}{a})}^{2} + {(\frac{n π}{b})}^{2}}

( 3.1A.13 )

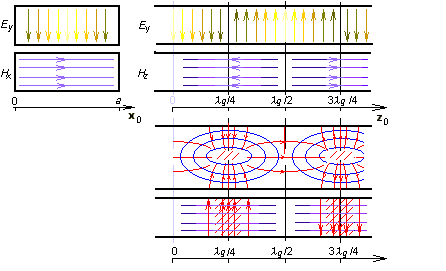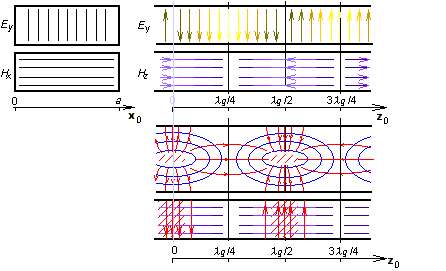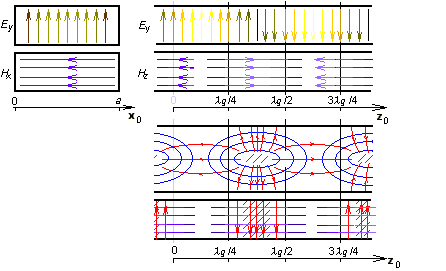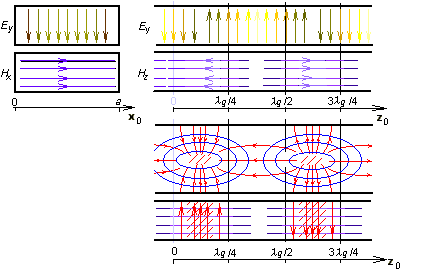
V této rovnici se permitivita a permeabilita vztahují k prostředí uvnitř vlnovodu, a je šířka obdélníkového vlnovodu a b je jeho výška. Celočíselné koeficienty m a n nazýváme vidovými čísly. Se zvyšováním vidových čísel roste kritický kmitočet (vyšší vidy vznikají na vyšších frekvencích).

Přelaďujme postupně generátor, napájející vlnovod, od nižších k vyšším kmitočtům a sledujme co se bude dít. Po překročení kritického kmitočtu nejnižšího vidu se bude vlnovodem šířit jediná vlna. Jakmile však překročíme kritický kmitočet následujícího vidu, budeme mít ve vlnovodu dvě vlny dvou různých vidů. Tyto vlny spolu interferují, což může způsobit mnohé komplikace. Proto jsou vlnovody provozovány téměř výhradně v pásmu jednovidovosti. Dolní kmitočet tohoto pásma je dán kritickým kmitočtem nejnižšího vidu, horní kmitočet je roven kritické frekvenci vidu následujícího. Vid s nejnižším kritickým kmitočtem je nazýván dominantním videm.

Závěrem si popišme siločáry dominantního vidu TE₁₀ v okamžiku t = t₀ (obr. s animací).

Obr. 3.1A.5

Vid TE₁₀

Kdybychom vlnovod podélně rozřízli rovinou kolmou na širší stranu, uviděli bychom harmonický průběh příčné složky elektrické intenzity E_y. Maximální intenzita se na obrázku nachází v místech z = λ_g/4 a z = 3λ_g/4 (zde má však opačnou fázi). Nulová je intenzita v místech z = 0 a z = λ_g/2. V místech maximální elektrické intenzity E_y je nulová podélná složka H_z a maximální příčná složka H_x magnetické intenzity. V příčném řezu v místě z = λ_g/4 je elektrická intenzita E_y největší uprostřed a nulová na okrajích (splněna okrajová podmínka). Příčná složka magnetické intenzity H_x je v z = λ_g/4 v příčném řezu konstantní.

Provedeme-li podélný řez rovinou kolmou na užší stranu vlnovodu, budou se nám siločáry magnetické intenzity jevit jako elipsy. Jejich tvar připomíná siločáry magnetické intenzity přímého vodiče, protékaného vysokofrekvenčním vodivým proudem. V případě vlnovodu je zdroj těchto siločar podobný – je jím posuvný proud, tekoucí dielektrikem vlnovodu ze spodní strany pláště vlnovodu na horní (z = 0) a naopak (z = λ_g /2). Omezme se na první případ. Když posuvný proud dorazí na horní stranu pláště, odtéká ve formě vodivého proudu po vnitřní straně pláště jednak zpět dolů, jednak ve vodorovném směru k sousedním ústím posuvného proudu. V obou případech jsou siločáry proudové hustoty J uzavřené.

Závěrem upozorněme na skutečnost, že elektromagnetické pole v příčném směru musí být rozloženo takovým způsobem, aby byly splněny okrajové podmínky na dokonale elektricky vodivých stěnách vlnovodu (tečné složky vektoru elektrické intenzity musejí být nulové a derivace tečných složek vektoru magnetické intenzity podle normály ke stěně musejí být rovněž rovny nule). Tuto skutečnost ilustruje matlabovský program pro analýzu obdélníkového vlnovodu pomocí metody konečných prvků. Uživatelský popis programu je uveden ve vrstvě C. Krátký úvod do metody konečných prvků a popis softwarové implementace je uveden ve vrstvě D.