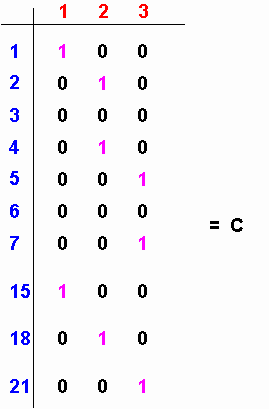3.1 VlnovodyVývoj programu
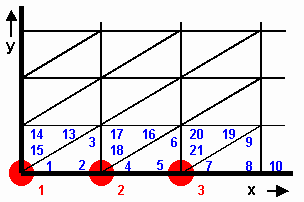 |
| Obr. 3.1D.1 | Příklad dvojrozměrné sítě konečných prvků. Modrá čísla: lokální uzly. Červená čísla: globální uzly. |
|
Metoda konečných prvků je obecná numerická
metoda pro řešení parciálních diferenciálních rovnic. Jelikož Maxwellovy rovnice, které popisují šíření elektromagnetické vlny
ve vlnovodu, patří do rodiny parciálních diferenciálních rovnic, můžeme metodu konečných prvků k analýze pole ve vlnovodu použít.
Základní postup při výpočtu rozložení pole ve vlnovodu lze shrnout do několika kroků:
- Profil vlnovodu rozdělíme na konečné prvky. V případě podélně homogenního vlnovodu rozdělíme profil na malé
trojúhelníky. Každý trojúhelník je konečný prvek, vrcholy trojúhelníků nazýváme uzly.
- Rozložení podélné složku elektrické intenzity u vidů TM a magnetické intenzity u vidů TE formálně aproximujeme
nad každým konečným prvkem lineární, kvadratickou nebo kubickou funkcí. Formální aproximací rozumíme skutečnost, že funkce je
vyjádřena pomocí neznámých hodnot intenzity v uzlech a pomocí známých bázových funkcí (lineárních, kvadratických, kubických).
Každá bázová funkce nabývá jednotkové hodnoty v jednom uzlu a nulové hodnoty v uzlech ostatních. Aproximace je formálně jednou
rovnicí pro N neznámých uzlových hodnot.
- Formální aproximaci dosadíme do výchozího vztahu, tj. do řešené rovnice. Jelikož aproximace díky své přibližnosti
nesplňuje řešenou rovnici zcela přesně, musíme k našemu vztahu přičíst chybovou funkci (tzv. reziduum). Čím menší je reziduum,
tím přesnější je aproximace.
- Reziduum minimalizujeme metodou vážených reziduí. Tato metoda spočívá v postupném vynásobením rezidua vhodnými váhovými
funkcemi a v integrování tohoto součinu přes celý profil analyzovaného vlnovodu. Zvolíme-li za váhové funkce bázové funkce
všech uzlů, v nichž neznáme hodnotu intenzity, dostaneme N rovnic pro N neznámých. Popsaná volba váhových funkcí
je nazývána Galerkinovou metodou.
- Vyřešíme maticovou rovnici, kterou dostaneme jako výsledek Galerkinovy metody. Tím získáme hodnoty doposud neznámých
uzlových intenzit. Maticová rovnice, kterou řešíme v případě vlnovodu, je tzv. zobecněný problém vlastních čísel. Výsledkem je
vektor vlastních čísel (vektor kvadrátů kritických vlnových čísel jednotlivých vidů) a matice odpovídajících vlastních vektorů
(uzlové hodnoty podélných složek intenzit jednotlivých vidů).
- Dosazením uzlových hodnot do formální aproximace získáme aproximační funkci hledané podélné složky intenzity v každém bodě
profilu analyzovaného vlnovodu. Z podélné složky intenzity můžeme vypočíst všechny ostatní složky vektorů intenzity elektrického
i magnetického pole.
Při praktických výpočtech metodou konečných prvků postupujeme poněkud odlišně. V literatuře jsou totiž k dispozici
již hotové matice koeficientů pro normovaný konečný prvek. Stačí nám vzít tyto matice koeficientů, upravit je pro naše konkrétní
prvky a spojit tyto matice společně s konečnými prvky do sítě. Celou proceduru lze opět popsat v několika krocích:
- Profil vlnovodu rozdělíme na konečné prvky. Tento úkol je naprosto shodný
s předchozím postupem.
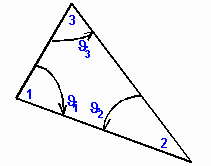 |
| Obr. 3.1D.2 | Dvojrozměrný konečný prvek pro lineární aproximaci |
|
- V literatuře nalezneme vztahy pro výpočet koeficientů jednotlivých konečných prvků. Dosazením plochy e-tého
konečného prvku A(e) a úhlů u vrcholů e-tého trojúhelníkového prvku (viz obr. 2) do těchto vztahů
dostaneme koeficienty pro naše konkrétní prvky. Vztahy pro matice koeficientů lineární aproximace následují:
|
,
,
,
,
|
( 3.1D.1 )
|
- Sestavíme diagonální matice pro "izolované" konečné prvky, tj. pro prvky dosud nespojené do sítě (symboly 0 značí nulové
matice o rozměrech 3x3)
|
,
|
( 3.1D.2 )
|
- Sestavíme vazební matici, která určuje vzájemný vztah mezi lokálními uzly (modrá čísla v obr. 1) a uzly globálními
(červená čísla v obr. 1). Sloupce matice odpovídají globálním uzlům, řádky matice uzlům lokálním. Pokud má být lokální uzel přidružen
k příslušnému uzlu globálnímu, napíšeme do řádku odpovídajícího číslu lokálního uzlu ve sloupci odpovídajícím uzlu globálnímu
hodnotu 1. V opačném případě je hodnota prvku matice nulová. Pro uzly z obr. 1 by vazební matice vypadala následovně:
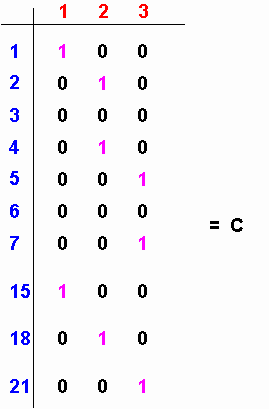 |
| Obr. 3.1D.3 | Vazební matice |
|
- Sdružíme nezávislé konečné prvky do propojené sítě elementů. Matematicky tomu odpovídají následující maticová
operace:
|
,
|
( 3.1D.3 )
|
- Vyřešením maticové rovnice (je stejná jako u dříve popsaného postupu)
získáme kritická vlnová čísla jednotlivých vidů k a uzlové hodnoty intenzity elektrického pole E těchto vidů.
Dosazením uzlových hodnot do formální aproximace získáme aproximační funkci hledané podélné složky intenzity v každém bodě
profilu analyzovaného vlnovodu.
Náš matlabovský program je založen na právě popsaném algoritmu. Zjednodušený výpis matlabovského kódu následuje. Jelikož
kód je pečlivě komentován, nebudeme ho dále nijak popisovat.
function kn = linearTE( Nx, Ny); iNx = Nx + 1; iNy = Ny + 1;
a = 22.86e-3;
b = 10.16e-3;
dx = ones(1,Nx) * (a/Nx);
dy = ones(1,Ny) * (b/Ny);
Q1 = [ 0 0 0; 0 1 -1; 0 -1 1] / 2;
Q3 = [ 1 -1 0; -1 1 0; 0 0 0] / 2;
Te = [ 2 1 1; 1 2 1; 1 1 2] /12;
N = 2 * Nx * Ny;
St = sparse( 3*N, 3*N);
Tt = sparse( 3*N, 3*N); n = 0; for ny=1:Ny
for nx=1:Nx
n = n + 1;
lw = 3*n-2;
hg = 3*n;
St(lw:hg,lw:hg) = Q1 * dx(nx)/dy(ny) + Q3 * dy(ny)/dx(nx);
Tt(lw:hg,lw:hg) = Te * dx(nx)*dy(ny)/2;
St(lw+3*Nx:hg+3*Nx,lw+3*Nx:hg+3*Nx) = St(lw:hg,lw:hg);
Tt(lw+3*Nx:hg+3*Nx,lw+3*Nx:hg+3*Nx) = Tt(lw:hg,lw:hg);
endn = n + Nx;
endC = get_c1( Nx, Ny, N) S = C'*St*C;
T = C'*Tt*C; clear C St Tt
[H,K] = eig( full(S), full(T));
kn = sqrt( diag( K));
|