3.2 Stíněné mikropáskové vedení

Základní teorie

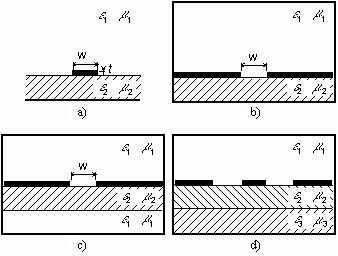
Obr. 3.2A.1

Vybrané typy planárních mikrovlnných vedení: a) otevřené mikropáskové vedení, b) stíněné štěrbinové vedení, c) ploutvové vedení, d) stíněné koplanární vedení

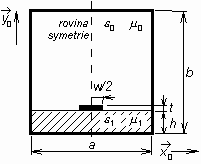
Stíněné mikropáskové vedení je členem rodiny planárních mikrovlnných vedení. Mezi často používaná planární vedení patří např. otevřené mikropáskové vedení (open microstrip line, obr. 3.2A.1a), stíněné štěrbinové vedení (shielded slotline, obr. 3.2A.1b), ploutvové vedení (shielded finline, obr. 3.2A.1c) či stíněné koplanární vedení (coplanar waveguide, obr. 3.2A.1d).

Z úseků planárních vedení je možno sestavovat mikrovlnné obvody. Planární vodiče přitom mohou sloužit k vzájemnému propojení komponentů, z nichž obvod sestává, nebo je možné využít je k realizaci pasivních obvodových prvků, zejména kapacitorů a induktorů. Navíc lze planární obvody relativně snadno doplňovat aktivními prvky jako jsou tranzistory či diody. Proto je v současnosti planární technologie v mikrovlnné technice velmi rozšířena a proto stále více nabývá na důležitosti analýza a návrh planárních struktur.

V tomto článku se budeme zabývat výpočtem rozložení elektromagnetického pole v mikropáskovém stíněném vedení (obr. 3.2A.2), u něhož se parametry ve směru podélné osy nemění. Potom nám totiž stačí analyzovat jen dvojrozměrnou strukturu (příčný průřez vedením), což výrazně zjednodušuje výpočet [20].

Obr. 3.2A.2

Stíněné mikropáskové vedení (podélně homogenní)

I při takovém zjednodušení, jaké jsme právě popsali, dosud nejsme schopni exaktně analyticky vypočíst rozložení elektromagnetického pole na mikropáskovém stíněném vedení. Proto musíme k analýze využít numerické metody nebo metody přibližné. Všechny tyto metody přitom můžeme rozdělit do dvou základních skupin, a to na metody kvazi-statické (quasi-static methods) a metody vlnové (full-wave methods) [20].

Kvazi-statické metody jsou založeny na předpokladu, že dominantní vid vlny, šířící se podél mikropáskového vedení, je možno s dobrou přesností aproximovat příčně elektromagnetickou vlnou (transversal electromagnetic wave, TEM). Tento předpoklad lze ovšem použít jen na nízkých mikrovlnných kmitočtech (obvykle do 5 GHz), protože při zvyšování pracovního kmitočtu roste velikost podélných složek elektromagnetického pole, takže je nelze dále zanedbávat.

Pro analýzu planárních vedení na vyšších mikrovlnných kmitočtech tedy musíme použít tzv. vlnové metody (full-wave methods). Vlnové metody vycházejí z popisu elektromagnetického pole na vedení pomocí úplných, nezjednodušených Maxwellových rovnic. Jelikož vedení budeme analyzovat v ustáleném harmonickém stavu, budou mít Maxwellovy rovnice následující tvar

\nabla \times E = - j ω μ_{0} μ_{r} H

( 3.2A.1a )

\nabla \times H = + j ω ε_{0} ε_{r} E + σ E + J_{s}

( 3.2A.1b )

\nabla \cdot (ε_{0} ε_{r} E) = ρ

( 3.2A.1c )

\nabla \cdot (μ_{0} μ_{r} H) = 0

( 3.2A.1d )

Zde E značí vektor elektrické intenzity, H je vektor magnetické intenzity, operátor nabla je v kartézském souřadném systému dán vztahem

\nabla = x_{0} \frac{\partial}{\partial x} + y_{0} \frac{\partial}{\partial y} + z_{0} \frac{\partial}{\partial z}

J_S značí hustotu proudů, které jsou vnuceny analyzovanému systému zdroji, ω je úhlový kmitočet, ε₀ a μ₀ jsou permitivita a permeabilita vakua, ε_r a μ_r značí relativní permitivitu a permeabilitu dielektrika uvnitř analyzované struktury, ρ je objemová hustota volného náboje v dielektriku a σ měrná elektrická vodivost dielektrika.

Předpokládejme, že zdroje elektromagnetického pole jsou umístěny ve velké vzdálenosti od oblasti, v níž provádíme výpočet (pak jsou v oblasti analýzy vnucené proudy J_s nulové), že je v dielektriku obklopujícím mikropásek nulová objemová hustota náboje ρ, že prostředí ve stínicím vlnovodu je lineární a izotropní (permitivita a permeabilita jsou skaláry, jejichž hodnota nezávisí na velikosti příslušné intenzity), že dielektrikum vykazuje elektrické ztráty (reprezentováno měrnou elektrickou vodivostí σ) a že všechny kovové části (stínicí vlnovod, mikropásek) jsou dokonalými elektrickými vodiči.

Všechny uvedené předpoklady dosaďme do soustavy (3.2A.1). Poté vynásobme obě strany rovnice (3.2A.1a) vektorově zleva operátorem nabla. Tím dostaneme na pravé straně vztahu (3.2A.1a) rotaci vektoru magnetické intenzity, kterou nahradíme pravou stranou rovnice (3.2A.1b). Dojdeme tak ke vztahu

\nabla \times (\nabla \times E) = - j ω μ_{0} μ_{r} (σ + j ω ε_{0} ε_{r}) E

( 3.2A.2 )

Pokud označíme druhou mocninu vlnového čísla ve vakuu jako

k_{0}^{2} = - j ω μ_{0} j ω ε_{0}

( 3.2A.3 )

a komplexní relativní permitivitu dielektrika jako

\tilde{ε_{r}} = \frac{σ}{j ω ε_{0}} + ε_{r}

( 3.2A.4 )

můžeme vztah (3.2A.2) přepsat do tvaru

\nabla \times (\nabla \times E) - \tilde{ε_{r}} μ_{r} k_{0}^{2} E = 0

( 3.2A.5 )

Analyzované mikropáskové vedení umístíme do kartézského souřadného systému (souřadnice x a y v příčném směru, souřadnice z podélná). Potom můžeme říci, že se elektromagnetická vlna bude ve struktuře šířit ve směru podélné osy z (podél mikropásku) a že závislost vektoru elektrické intenzity na této podélné souřadnici bude popsána vztahem

E (x, y, z) = E (x, y) \exp (- γ z)

( 3.2A.6 )

kde γ je konstanta šíření (propagation constant)

γ = β + j α

;

( 3.2A.7 )

β je měrný útlum (attenuation constant) a α značí měrnou fázi (phase constant).

Matematický popis elektromagnetické vlny, šířící se ve směru osy z (3.2A.6), dosadíme do vektorové rovnice (3.2A.5). Potom můžeme vyčíslit všechny parciální derivace podle z (ty přejdou na násobení příslušného členu rovnice konstantou šíření se záporným znaménkem -γ). Vyjádříme-li navíc všechny vektory v rovnici (3.2A.5) jako součet vektoru příčného (index t jako transversal) a vektoru podélného (index z podle podélné osy)

E = E_{t} + z_{0} E_{z}

( 3.2A.8a )

\nabla = \nabla_{t} + z_{0} \frac{\partial}{\partial z} = \nabla_{t} - γ z_{0}

( 3.2A.8b )

dostáváme

\nabla_{t} \times (\nabla_{t} \times E_{t}) - γ (\nabla_{t} E_{z} + γ E_{t}) = k_{0}^{2} μ_{r} \tilde{ε_{r}} E_{t}

( 3.2A.9a )

\nabla_{t} \times [(\nabla_{t} E_{z} + γ E_{t}) \times z_{0}] = k_{0}^{2} μ_{r} \tilde{ε_{r}} E_{z} z_{0}

( 3.2A.9b )

Zatímco (3.2A.9a) je vektorovou rovnicí pro příčné složky vektorů, (3.2A.9b) je skalární rovnicí pro podélné složky vektorů.

Soustavu diferenciálních rovnic (3.2A.9) musíme doplnit okrajovými podmínkami, kterým musí řešení soustavy (3.2A.9) vyhovovat

\begin{array}{r} n_{0} \times E_{t} = 0 \\ E_{z} = 0 \end{array}} n a Γ_{1}

( 3.2A.10a )

\begin{array}{r} [\nabla_{t} E_{z} + γ E_{t}] \cdot n_{0} = 0 \\ \nabla_{t} \times E_{t} = 0 \end{array}} n a Γ_{2}

( 3.2A.10b )

Pomocí vztahu (3.2A.10a) vyjadřujeme skutečnost, že složky vektoru elektrické intenzity, které jsou tečné k dokonale elektricky vodivým povrchům Γ₁, musejí být na těchto površích nulové. Vztah (3.2A.10b) pak říká, že změna složek vektoru elektrické intenzity ve směru normály k dokonalému magnetickému povrchu Γ₂ musí být na tomto povrchu nulová.

Rovnice (3.2A.9), doplněné okrajovými podmínkami (3.2A.10), budou výchozími vztahy pro vlnovou analýzu našeho stíněného mikropáskového vedení. Musíme si však uvědomit, že v soustavě (3.2A.9), (3.2A.10) máme zahrnutu pouze první a druhou Maxwellovou rovnici, takže u získaných řešení musíme kontrolovat, zda vyhovují rovněž třetí a čtvrté Maxwellově rovnici. Kdyby tomu tak nebylo, získané řešení by bylo řešením fyzikálně neexistujícím (spurious solution).

V následujících odstavcích popíšeme, jak lze analýzu stíněného mikropáskového vedení, která vychází ze vztahů (3.2A.9), (3.2A.10), implementovat pomocí metody konečných prvků.

Dříve, než se pustíme do analýzy stíněného mikropáskového vedení metodou konečných prvků, budeme se chvíli věnovat popisu fyzikálních dějů, které v této struktuře probíhají. Aby totiž byla numerická analýza elektromagnetického pole úspěšná, musejí být všechny děje korektně modelovány.

Začněme u obdélníkového vlnovodu, v němž je vakuum. V něm se šíří vlny příčně elektrické (přítomna podélná složka magnetické intenzity) a vlny příčně magnetické (přítomna podélná složka intenzity elektrické). Pokud však do vakua ve vlnovodu vložíme dielektrický substrát (výplň se stane nehomogenní), budou ve vlnovodu přítomny podélné složky elektrické i magnetické intenzity současně. Kdyby tomu tak totiž nebylo, nebyly by splněny podmínky spojitosti na rozhraní dielektrika a vakua.

Šíření elektromagnetické vlny ve vlnovodu s nehomogenní výplní může být popsáno pomocí hybridních módů LSM (Longitudinal Section Magnetic) a LSE (Longitudinal Section Electric). Jestliže však navíc doplníme tuto nehomogenní výplň kovovým mikropáskem, jsou na tomto pásku indukovány příčné a podélné proudy, které mezi módy LSE a LSM způsobují vzájemnou vazbu.

Numerická analýza šíření elektromagnetických vln v kovovém vlnovodu vyplněném vakuem je relativně snadná, neboť při ní stačí řešit homogenní vlnovou rovnici buď pro podélnou složku elektrické intenzity (vidy TM) nebo pro podélnou složku intenzity magnetické (vidy TE). Pokud však přejdeme k numerické analýze mikropáskového vedení, musíme věnovat pozornost dvěma potenciálním zdrojům fyzikálně neexistujících řešení.

První příčinou vzniku fyzikálně neexistujících řešení je nekorektní modelování elektromagnetických poměrů na rozhraní mezi substrátem a vakuem, druhou příčinou pak může být nekorektní modelování vlivu kovových pásků. Obě ze zmíněných příčin lze odstranit použitím tzv. hybridních konečných prvků.

Při analýze stíněného mikropáskového vedení pomocí hybridních konečných prvků musíme zahrnout do výpočtů všechny složky elektrické intenzity nebo všechny složky intenzity magnetické. Výchozím vztahem analýzy přitom je (3.2A.9).

Podstata hybridních konečných prvků spočívá v modelování podélné složky elektrické nebo magnetické intenzity pomocí uzlové aproximace a v modelování příčných složek elektrické nebo magnetické intenzity pomocí aproximace, založené na hranových vektorech (edge vectors).

Věnujme se nejdříve obecnému postupu řešení (3.2A.9) za podmínek (3.2A.10) pomocí metody konečných prvků. U každého obecného kroku postupu si pak uvedeme, jak metoda pracuje v našem konkrétním případě (podélně homogenní stíněné mikropáskové vedení, analyzované pomocí hybridních konečných prvků.

V prvém kroku analyzovanou strukturu rozdělíme na podoblasti (konečné prvky, finite elements), které se vzájemně nepřekrývají a jejichž sjednocení zahrnuje všechny body analyzované oblasti. V prostoru konečného prvku musejí být parametry analyzované struktury (permitivita, permeabilita, vodivost) konstantní. Na velikost a na tvar konečných prvků přitom nejsou kladena žádná omezení. Síť konečných prvků (finite-element mesh) může být hustější v oblasti, v níž nás zajímají detaily řešení, a může být relativně řídká tam, kde nás detaily řešení nezajímají. Konečné prvky mohou být křivočaré, takže lze s jejich pomocí modelovat systémy s libovolnou geometrií.

Při analýze podélně homogenního mikropáskového vedení řešíme dvojrozměrný problém (v podélném směru se vlastnosti vedení nemění). Budeme se proto zabývat jen dvojrozměrnými konečnými prvky. Pomineme-li po částech konstantní aproximaci, je nejjednodušší aproximační funkcí funkce lineární. V případě dvojrozměrných konečných prvků je lineární aproximací rovina, ležící nad těmito prvky. Můžeme si představit, že hledaná veličina je vynášena kolmo k nákresně nad každý konečný prvek.

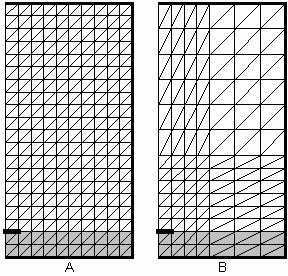
Obr. 3.2A.3

Příklady sítí obdélníkových dvojprvků pro analýzu stíněného mikropáskového vedení

Jelikož rovina je jednoznačně určena třemi body, je vhodné rozdělit analyzovanou oblast na trojúhelníkové konečné prvky a souřadnice vrcholů těchto trojúhelníkových prvků vzít jako nezávislé proměnné dvojrozměrné lineární aproximace. Závislými funkčními hodnotami ve vrcholech pak budou vzorky hledaného rozložení pole. Proložením roviny těmito závislými funkčními hodnotami ve vrcholech trojúhelníkového konečného prvku dostaneme jednoznačně určenou aproximační rovinu.

Rozdělení analyzované oblasti na konečné prvky je třeba věnovat velkou pozornost, neboť jak výsledná chyba řešení dané parciální diferenciální rovnice tak výpočetní čas, nutný k vyřešení problému, silně závisejí na geometrii sítě.

Na obr. 3.2A.3 jsou uvedeny příklady dvou trojúhelníkových sítí pro analýzu stíněného mikropáskového vedení. Pro jednoduchost vždy dva trojúhelníkové konečné prvky společně vytvářejí obdélníkový dvojprvek, který je pak v našem případě základním stavebním kamenem sítě.

Síť A je homogenní (sestává se z identických konečných prvků). Jelikož můžeme předpokládat, že velikost elektromagnetického pole velmi rychle klesá se vzdáleností od mikropásku, lze pokrýt vzdálenější oblast mnohem řidší sítí B. Jak ukážeme dále, tato volba se na jednu stranu pouze nepatrně projeví na výsledcích výpočtu, avšak na druhou stranu ušetříme významné množství výpočetního času (menší počet konečných prvků přirozeně znamená menší počet matematických operací).

V druhém kroku řešení formálně vyjádříme aproximaci hledané neznámé funkce nad celou plochou jednoho každého konečného prvku. Obvykle přitom neznámé řešení aproximujeme lineární kombinací zvolených aproximačních funkcí a neznámých aproximačních koeficientů. Nejjednodušší aproximační funkcí je funkce lineární. Jako příklad si vezměme obecnou rovinu, jednoznačně určenou funkčními hodnotami aproximované funkce ve třech zvolených bodech konečného prvku.

Tuto obecnou rovinu můžeme složit ze tří dílčích rovin (lineární kombinace), nabývajících v jednom zvoleném bodě konečného prvku jednotkové hodnoty a ve zbývajících dvou zvolených bodech prvku hodnoty nulové. Neznámé aproximační koeficienty, vystupující v lineární kombinaci u dílčích rovin, potom mají význam jakýchsi prostorových vzorků (samples) prostorového rozložení počítané veličiny v bodě, v němž nabývá dílčí funkce hodnoty 1 (ostatní dílčí funkce jsou v tomto bodě nulové, a proto se na vzorkování nepodílejí. Pro podélnou složku vektoru elektrické intenzity tudíž můžeme psát

E_{z}^{(n)} (x, y) \approx \sum_{m = 1}^{M_{n}} c_{m} N_{m}^{(n)} (x, y)

( 3.2A.11 )

kde E_z⁽ⁿ⁾ je aproximace průběhu hledané funkce nad plochou n-tého konečného prvku, c_m jsou neznámé aproximační koeficienty a N_m⁽ⁿ⁾ jsou zvolené dílčí aproximační funkce na n-tém konečném prvku, M_n značí počet dílčích aproximačních funkcí, použitých pro sestavení aproximace hledané funkce nad plochou n-tého konečného prvku.

Sloučením aproximací nad všemi N konečnými prvky pak dostáváme celkovou (globální) aproximaci nad analyzovanou oblastí

\tilde{E_{z}} (x, y) \approx \sum_{n = 1}^{N} E_{z}^{(n)} (x, y)

( 3.2A.12 )

Vztah (3.2A.12) je jedinou rovnicí o M neznámých aproximačních koeficientech c_m. Podaří-li se nám tyto neznámé koeficienty nalézt, získáme aproximaci rozložení hledané veličiny v celé analyzované oblasti.

Více informací o vhodných dílčích aproximačních funkcích a vysvětlení, jak je to s formální aproximací příčné složky vektoru elektrické intenzity, uvádíme ve vrstvě B.

V třetím kroku řešení dosadíme formální aproximaci řešení E_z^~ do výchozí parciální diferenciální rovnice. Jelikož se jedná o aproximaci řešení a ne o řešení zcela přesné, není tato rovnice splněna dokonale. Tuto skutečnost respektujeme zavedením zbytkové funkce (rezidua), která je rovna rozdílu mezi přesným řešením parciální diferenciální rovnice a mezi jeho aproximací

R (x, y) = \tilde{E} (x, y) - E (x, y)

( 3.2A.13 )

Aproximace bude přirozeně tím přesnější, čím menších hodnot bude nabývat zbytková funkce. Proto se budeme snažit zbytkovou funkci minimalizovat, a to přes celou zkoumanou oblast. Jednou z možností, která se nám pro minimalizaci nabízí, je metoda vážených reziduí (method of weighted residuals).

Postupujeme-li podle metody vážených reziduí, musíme vynásobit reziduum R(x, y) vhodnou váhovou (weighting) funkcí W(x, y). Získaný součin potom integrujeme přes celou zkoumanou oblast S a výsledek položíme roven nule

\int_{S} R (x, y) W (x, y) d S = 0

( 3.2A.14 )

kde dS = dx dy.

Použitím tolika různých, vhodně zvolených váhových funkcí W_n, kolik je neznámých aproximačních koeficientů, dostaneme lineární soustavu se stejným počtem rovnic, jaký je počet neznámých koeficientů. Vyřešením této soustavy neznámé aproximační koeficienty jednoznačně určíme. Volíme-li postupně za váhové funkce dílčí aproximační funkce těch uzlů, v nichž neznáme podélnou složku vektoru elektrické intenzity, mluvíme o Galerkinově metodě.

Výsledná maticová rovnice bude mít v našem případě pro n-tý konečný prvek tvar

[\begin{matrix} S_{t}^{(n)} - k_{0}^{2} μ_{r}^{(n)} {\tilde{ε}}_{r}^{(n)} T_{t}^{(n)} & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} E_{t}^{(n)} \\ E_{z}^{(n)} \end{matrix}] = γ^{2} [\begin{matrix} T_{t}^{(n)} & G^{(n)} \\ G^{{(n)}^{T}} & S_{z}^{(n)} - k_{0}^{2} μ_{r}^{(n)} {\tilde{ε}}_{r}^{(n)} T_{z}^{(n)} \end{matrix}] [\begin{matrix} E_{t}^{(n)} \\ E_{z}^{(n)} \end{matrix}]

kde

T_{t}^{(n)} E_{t}^{(n)} = \sum_{i, j} {e_{t, i j}^{(n)} \iint_{S^{(n)}} [N_{t, r s}^{(n)} \cdot N_{t, i j}^{(n)}] d S}

( 3.2A.15a )

G^{(n)} E_{z}^{(n)} = \sum_{m} {e_{z, m}^{(n)} \iint_{S^{(n)}} [N_{t, r s}^{(n)} \cdot (\nabla_{t} N_{z, m}^{(n)})] d S}

( 3.2A.15b )

S_{z}^{(n)} E_{z}^{(n)} = \sum_{m} {e_{z, m}^{(n)} \iint_{S^{(n)}} [(\nabla_{t} N_{z, q}^{(n)}) \cdot (\nabla_{t} N_{z, m}^{(n)})] d S}

( 3.2A.15c )

T_{z}^{(n)} E_{z}^{(n)} = \sum_{m} {e_{z, m}^{(n)} \iint_{S^{(n)}} [N_{z, q}^{(n)} N_{z, m}^{(n)}] d S}

( 3.2A.15d )

S_{t}^{(n)} E_{t}^{(n)} = \sum_{i, j} {e_{t, i j}^{(n)} \iint_{S^{(n)}} [(\nabla_{t} \times N_{t, r s}^{(n)}) \cdot (\nabla_{t} \times N_{t, i j}^{(n)})] d S}

( 3.2A.15e )

Ve výše uvedených vztazích je E_t⁽ⁿ⁾ sloupcový vektor tří neznámých hranových aproximačních koeficientů (pro aproximaci příčných složek vektoru elektrické intenzity) na ploše n-tého konečného prvku a E_z⁽ⁿ⁾ značí sloupcový vektor tří neznámých uzlových aproximačních koeficientů (pro aproximaci podélné složky vektoru elektrické intenzity) opět na n-tém konečném prvku. Dále, γ značí komplexní konstantu šíření, k₀ je vlnové číslo ve vakuu, μ_r⁽ⁿ⁾ je relativní permeabilita n-tého konečného prvku a ε^~_r⁽ⁿ⁾ je komplexní relativní permitivita téhož prvku. Symbol dS značí elementární plošku pro integraci po ploše n-tého konečného prvku a symbol S⁽ⁿ⁾ vyjadřuje celkovou plochu n-tého konečného prvku. Suma se sčítacím indexem m symbolizuje sčítání přes všechny uzly konečného prvku (tj. m = 0, 1, 2) a suma s indexy i, j znamená sčítání přes všechny hrany prvku (tj. i, j = 0-1, 1-2, 2-0). Symboly e_{t, ij}⁽ⁿ⁾ jsou hranové aproximační koeficienty, symboly e_{z, m}⁽ⁿ⁾ jsou aproximační koeficienty uzlové.

Matice T_t⁽ⁿ⁾, G⁽ⁿ⁾, S_z⁽ⁿ⁾, T_z⁽ⁿ⁾ a S_t⁽ⁿ⁾ jsou matice koeficientů n-tého konečného prvku o rozměru 3 × 3. Elementy zmíněných matic byly vypočteny integrací součinu dílčích aproximačních a váhových funkcí (nebo jejich derivací) na ploše n-tého konečného prvku. Tyto matice můžeme vyčíslit pomocí následujících vztahů

S_{t}^{(n)} = \frac{1}{A^{(n)}} [\begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix}]

( 3.2A.16a )

T_{t}^{(n)} = \frac{1}{12} \sum_{i = 0}^{2} Q_{i} c o t g [θ_{i}^{(n)}]

( 3.2A.16b )

G^{(n)} = \frac{1}{6} \sum_{i = 0}^{2} C_{i} c o t g [θ_{i}^{(n)}]

( 3.2A.16c )

S_{z}^{(n)} = \frac{1}{2} \sum_{i = 0}^{2} D_{i} c o t g [θ_{i}^{(n)}]

( 3.2A.16d )

T_{z}^{(n)} = \frac{A^{(n)}}{12} [\begin{matrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{matrix}]

( 3.2A.16e )

kde

Q_{0} = [\begin{matrix} 3 & - 1 & - 1 \\ - 1 & 1 & 1 \\ - 1 & 1 & 1 \end{matrix}], Q_{1} = [\begin{matrix} 1 & - 1 & 1 \\ - 1 & 3 & - 1 \\ 1 & - 1 & 1 \end{matrix}], Q_{2} = [\begin{matrix} 1 & 1 & - 1 \\ 1 & 1 & - 1 \\ - 1 & - 1 & 3 \end{matrix}],

C_{0} = [\begin{matrix} 0 & - 2 & 2 \\ 0 & 1 & - 1 \\ 0 & 1 & - 1 \end{matrix}], C_{1} = [\begin{matrix} - 1 & 0 & 1 \\ 2 & 0 & - 2 \\ - 1 & 0 & 1 \end{matrix}], C_{2} = [\begin{matrix} 1 & - 1 & 0 \\ 1 & - 1 & 0 \\ - 2 & 2 & 0 \end{matrix}],

D_{0} = [\begin{matrix} 0 & 0 & 0 \\ 0 & 1 & - 1 \\ 0 & - 1 & 1 \end{matrix}], D_{1} = [\begin{matrix} 1 & 0 & - 1 \\ 0 & 0 & 0 \\ - 1 & 0 & 1 \end{matrix}], D_{2} = [\begin{matrix} 1 & - 1 & 0 \\ - 1 & 1 & 0 \\ 0 & 0 & 0 \end{matrix}],

A⁽ⁿ⁾ je plocha n-tého konečného prvku a θ_i⁽ⁿ⁾ je úhel u i-tého vrcholu n-tého konečného prvku. Uvedené vztahy přitom platí pro následující organizaci uzlů a hran

E^{(n)} = {[\begin{matrix} e_{z,0}^{(n)} & e_{z,1}^{(n)} & e_{z,2}^{(n)} & e_{t,12}^{(n)} & e_{t,20}^{(n)} & e_{t,01}^{(n)} \end{matrix}]}^{T}

( 3.2A.16f )

Vyřešením maticové rovnice pro vektor neznámých aproximačních koeficientů získáme řešení problému. Dosazením aproximačních koeficientů do formální aproximace dostaneme skutečnou aproximaci hledané funkce v každém bodě n-tého konečného prvku, sjednocením aproximací nad všemi konečnými prvky pak získáme globální aproximaci ve všech bodech prostoru, nad kterým jsme hledali řešení zadané parciální diferenciální rovnice.

Ve vrstvě C nabízíme čtenáři matlabovský program, který pomocí právě popsané verze metody konečných prvků analyzuje stíněné mikropáskové vedení. Praktický programátorský popis programu uvádíme ve vrstvě D.