4.1 Drátový dipól

Základní teorie

V této kapitole se seznámíme s výpočtem parametrů drátového dipólu pomocí momentové metody. Veškeré informace se snažíme co nejsrozumitelněji vysvětlit ve vrstvě A. Vrstvu B v tomto případě využíváme k uvedení anglické verze této kapitoly. Činíme tak proto, abychom čtenáře seznámili s anglickou terminologií, využívanou v oblasti antén a numerických metod.

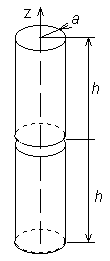
Obr. 4.1A.1

Drátový dipól

Všechny důležité technické parametry antén, jakými jsou např. zisk, vstupní impedance nebo směrová charakteristika, mohou být relativně snadno vypočteny, pokud známe rozložení proudu na anténním vodiči. Výpočet rozložení proudu je však bohužel dosti komplikovaný, protože při jeho určování je třeba řešit integrální rovnice.

K řešení integrálních rovnic existují dva základní přístupy – iterační a momentový. Iterační metody vycházejí z hrubé aproximace proudového rozložení (uvažujeme např. sinusové rozložení proudu na drátovém dipólu), která je iteračně zpřesňována. Oproti tomu momentové metody převádějí řešení integrální rovnice na řešení soustavy rovnic lineárních, s nimiž si bez problémů poradí např. Matlab.

V této kapitole naší učebnice se budeme zabývat pouze momentovou analýzou drátových antén. Ve všech případech budeme předpokládat, že anténa je tvořena kruhovým válcem o poloměru a a že je dlouhá 2h. Osu anténního vodiče umístíme do osy z (obr. 4.1A.1) válcového souřadného systému (r, ρ, z). Dále předpokládáme, že se anténa nachází ve vakuu (μ = μ₀, ε = ε₀, σ = 0) a že veškeré možné ztráty jsou nulové.

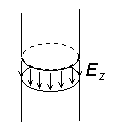
Obr. 4.1A.2

Budicí elektrické pole ve vstupní štěrbině

Uprostřed anténního vodiče (z = 0) budeme uvažovat krátkou štěrbinku. Tuto štěrbinku připojíme k hypotetickému harmonickému zdroji, který vytváří rotačně souměrné budicí pole (obr. 4.1A.2). Napětí ve štěrbince pak můžeme popsat vztahem

V = - \int_{g a p} E_{z} d z

( 4.1A.1 )

Dále předpokládáme, že toto napětí je rovno jednomu voltu. Ve vztahu (4.1A.1) značí E_z z-ovou složku intenzity budícího elektrického pole ve štěrbině, a tedy i na (válcovém) povrchu této krátké části antény (obr. 4.1A.2). Mimo štěrbinu je E_z nulové, protože předpokládáme dokonalou elektrickou vodivost vodiče antény.

I. Momentová metoda

Uvažujme obecnou integrální rovnici ve tvaru

\int_{a}^{b} f (z, ξ) d ξ = g (z)

( 4.1A.2 )

kde f je neznámá funkce (v našem případě rozložení proudu na anténě), <a,b> značí analyzovanou oblast a g je známá funkce, popisující působení zdrojů. Momentové řešení rovnice (4.1A.2) potom můžeme rozepsat do následujících tří kroků:

Neznámou funkci f aproximujeme pomocí lineární kombinace známých bázových funkcí f_n a neznámých koeficientů c_n
$f \approx \tilde{f} = \sum_{n = 1}^{N} c_{n} f_{n}$ . ( 4.1A.3 )
Formální aproximaci (formální proto, že neznáme koeficienty c_n) hledané funkce f^~ dosadíme zpět do řešené rovnice a zaměníme pořadí sčítání a integrování
$\sum_{n = 1}^{N} c_{n} \int_{a}^{b} f_{n} (z, ξ) d ξ = g (z) + R (z)$ . ( 4.1A.4 )
V uvedeném vztahu značí R(z) tzv. reziduum, které vyjadřuje skutečnost, že aproximace řešení f^~ není identická se zcela přesným řešením rovnice. Vztah (4.1A.4) je jednou rovnicí pro N neznámých koeficientů c_n.
Co možná nejpřesnější aproximaci řešení získáme tehdy, když reziduum R bude minimální. Reziduum tudíž minimalizujeme tzv. metodou vážených reziduí: součin vhodné váhové funkce w a rezidua R, integrovaný přes analyzovanou oblast <a, b> musí být nulový [5]. Pokud pro váhování postupně použijeme N různých váhových funkcí, získáme soustavu N lineárních rovnic pro N neznámých koeficientů c_n
$\int_{a}^{b} w_{m} (z) R (z) d z = 0 m = 0,1,... N$ , ( 4.1A.5a )

$\sum_{n = 1}^{N} c_{n} \int_{a}^{b} w_{m} (z) \int_{a}^{b} f_{n} (z, ξ) d ξ d z = \int_{a}^{b} w_{m} (z) g (z) d z$ . ( 4.1A.5b )
Jak váhové funkce tak funkce bázové musejí být lineárně nezávislé na intervalu <a,b>.

II. Bázové funkce

Bázové funkce mohou globální nebo lokální povahu. Globální bázové funkce jsou definovány přes celou analyzovanou oblast <a,b>. Např. soustava funkcí

f_{n} (z) = \cos (\frac{π n z}{h})

( 4.1A.6 )

Obr. 4.1A.3

Vícebázová aproximace a) po částech konstantní, b) po částech lineární

je lineárně nezávislá na <a,b> a koeficienty c_n

f (z) \approx \tilde{f} (z) = \sum_{n = 1}^{N} c_{n} f_{n} = \sum_{n = 1}^{N} c_{n} \cos (\frac{π n z}{h})

( 4.1A.7 )

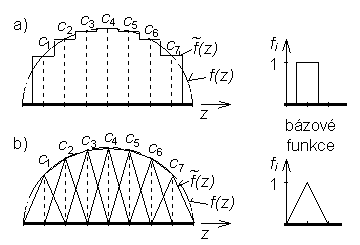
zde mají význam Fourierových koeficientů proudového rozložení.

Aproximaci založenou na globálních bázových funkcích nazýváme jednobázovou aproximací.

Lokální bázové funkce jsou definovány přes celou analyzovanou oblast také, avšak pouze na určité podoblasti nabývají nenulové funkční hodnoty (obr. 4.1A.3). Pokud jsou bázové funkce normovány (tzn. pokud se jejich funkční hodnota mění od nuly do jedničky), pak koeficienty c_n mají význam uzlových hodnot (vzorků) hledané funkce f (obr. 4.1A.3). Aproximaci založenou na lokálních bázových funkcích nazýváme vícebázovou aproximací.

III. Váhové funkce

Mezi nejčastěji používané přístupy k minimalizaci rezidua patří kolokační metoda a metoda Galerkinova.

Kolokační metoda využívá k váhování Diracovy impulsy, umístěné do bodů, v nichž počítáme hodnoty neznámého proudového rozložení

w_{m} (z) = δ (z - z_{m})

( 4.1A.8 )

Kolokační metoda vykazuje velmi nízké výpočetní nároky, jelikož díky filtrační vlastnosti Diracových impulsů je jedna integrace eliminována

\sum_{n = 1}^{N} c_{n} \int_{a}^{b} f_{n} (z_{m}, ξ) d ξ = g (z_{m})

( 4.1A.9 )

Na druhou stranu je minimalizace rezidua vztažena pouze k bodům z_m, do nichž byly umístěny váhovací impulsy.

Galerkinova metoda využívá k váhování funkce, které jsou identické s funkcemi bázovými

w_{m} (z) = f_{m} (z)

( 4.1A.10 )

Galerkinova metoda vykazuje ve srovnání s metodou kolokační vyšší výpočetní nároky protože v jejím případě k eliminaci jednoho integrování nedochází. Na druhou stranu jsou však do procesu minimalizace rezidua zahrnuty všechny body analyzované oblasti z ∈ <a,b>.

IV. Drátové antény

Uvažujme drátovou anténu z obr. 4.1A.1. Potom můžeme vyzařované elektromagnetické pole popsat pomocí vektorového potenciálu A (popisuje působení proudů na anténě) a skalárního potenciálu φ [2]

\frac{\partial^{2} A_{z} (z)}{\partial z^{2}} + k^{2} A_{z} (z) = - μ_{0} J_{z} (z)

( 4.1A.11a )

\frac{\partial^{2} φ (z)}{\partial z^{2}} + k^{2} φ (z) = - \frac{ρ (z)}{ε_{0}}

( 4.1A.11b )

Zde J_z značí z-ovou složku proudové hustoty [A.m^-2], vnucenou anténě zdrojem, ρ je objemová hustota náboje [C.m^-3] na anténním vodiči, A_z značí z-ovou složku vektorového potenciálu, φ je skalární potenciál, k=2π/λ značí vlnové číslo a λ vlnovou délku.

Elektrony, které přitékají do antény jako proud, se hromadí na anténním vodiči jako náboj. V druhé polovině periody se směr proudu otočí a náboje z konců anténního vodiče odtékají zpět do zdroje. Jelikož náboje a proudy na anténě spolu souvisejí, musíme vzájemně je svázat. Činíme tak podmínkou kontinuity [2]

\frac{\partial J_{z} (z)}{\partial z} + j ω ρ (z) = 0

( 4.1A.12a )

Pokud je poloměr anténního vodiče mnohem menší než vlnová délka a << λ, potom můžeme předpokládat, že proudy a náboje jsou soustředěny na ose vodiče. Tento předpoklad je samozřejmě nesprávný (v důsledku povrchového jevu jsou náboje a proudy soustředěny na povrchu vodiče), avšak metoda i přes tento nesprávný předpoklad dává překvapivě dostatečně přesné výsledky [5]. Řešíme-li (s uvážením uvedeného chybného předpokladu) soustavu (4.1A.11), dostáváme [2]

A_{z} (z) = \frac{μ}{4 π} \int_{2 h} I_{z} (ξ) \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1A.12b )

φ (z) = \frac{1}{4 π ε} \int_{2 h} σ (ξ) \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1A.12c )

Zde I_z(ξ) značí proud [A] tekoucí v ose anténního vodiče, σ(ξ) je délková hustota náboje [C.m^-1] na ose anténního vodiče, R(z,ξ) je vzdálenost mezi pozicí ξ zdroje pole I_z(ξ) a σ(ξ), dále z je místo, v němž počítáme potenciály A(z) a φ(z). Známe-li potenciály A(z) a φ(z), můžeme vypočíst intenzitu vyzařovaného elektrického pole [2]

E_{z}^{s} (z) = - j ω A_{z} (z) - \frac{\partial φ (z)}{\partial z}

( 4.1A.12d )

Elektrická intenzita musí splňovat okrajovou podmínku na povrchu dokonale elektricky vodivého anténního vodiče S

E_{z}^{i} + E_{z}^{s} = 0

na S .

( 4.1A.12e )

E_zⁱ značí z-ovou složku (tj. složku tečnou k povrchu anténního vodiče) vektoru elektrické intenzity dopadající vlny. Dopadající vlna je vytvořena zdroji mimo vlastní anténu. Když analyzujeme anténu jako vysílací, je E_zⁱ intenzita vytvořená napájecím zdrojem v budicí štěrbině (E_z v obr. 4.1A.2). Když analyzujeme anténu jako přijímací, je E_zⁱ intenzita přijímaného vlnění (po celé délce vodiče).

Chceme-li určit rozložení proudu na anténě, musíme vyřešit soustavu (4.1A.12).

Abychom se mohli postarat o splnění okrajové podmínky (4.1A.12e), musíme počítat elektrickou intenzitu (a tudíž i potenciály A a φ) na povrchu anténního vodiče. Proto můžeme vzdálenost mezi zdroji pole (na ose) a místy pozorování (na povrchu vodiče) vyjádřit jako

R (z, ξ) = \sqrt{a^{2} + {(z - ξ)}^{2}}

( 4.1A.13 )

V dalších odstavcích budeme předpokládat po částech konstantní bázové funkce a Diracovy funkce váhové. S využitím těchto funkcí budeme hledat řešení soustavy (4.1A.12).

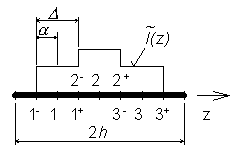
Obr. 4.1A.4

Po částech konstatní aproximace

V prvém kroku musíme analyzovanou anténu diskretizovat. Tato diskretizace je naznačena na obr. 4.1A.4. Dolní hranice segmentů je označena indexem ”-”, horní hranice indexem ”+”. Dolní hranice prvního segmentu a horní hranice posledního segmentu jsou posunuty o polovinu segmentu za konec anténního vodiče, aby bylo možno modelovat uzel proudu I(-h)=I(h)=0 na koncích antény. Délka všech segmentů je stejná Δ = 2α.

Dosadíme-li po částech konstantní aproximaci do (4.1A.12b,c), dostáváme

A_{z} (z) \approx \frac{μ}{4 π} \sum_{n = 1}^{N} I_{n} \int_{- h + (n - 0,5) Δ}^{- h + (n + 0,5) Δ} \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1A.14b )

φ (z) \approx \frac{1}{4 π ε} \sum_{n = 1}^{N} σ_{n} \int_{- h + (n - 0,5) Δ}^{- h + (n + 0,5) Δ} \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1A.14c )

Ve výše uvedených vztazích jsou I_n a σ_n uzlové hodnoty proudu a nábojové hustoty.

Jelikož první derivace po částech konstantní aproximace je nulová na konstantní části funkce a neexistuje na hranicích, derivace v (4.1A.12a) a (4.1A.12d) jsou nahrazeny konečnými diferencemi. Uvážíme-li že I_n = I_z (-h+nΔ), můžeme rovnici kontinuity přepsat do tvaru

\frac{I_{z} (- h + (n + 1) Δ) - I_{z} (- h + n Δ)}{Δ} + j ω σ (- h + (n + 0,5) Δ) \approx 0

( 4.1A.15a )

a vztah pro výpočet intenzity elektrického pole přechází na

E_{z}^{s} (- h + n Δ) \approx - j ω A_{z} (- h + n Δ) - \frac{φ [- h + (n + 0,5) Δ] - φ [- h + (n - 0,5) Δ]}{Δ}

( 4.1A.15d )

Vztahy (4.1A.15a) a (4.1A.15d) odpovídají skutečnosti, že Diracovy impulsy jsou při váhování umístěny do středu segmentu u vektorového potenciálu

A_{z} (- h + m Δ) \approx \frac{μ}{4 π} \sum_{n = 1}^{N} I_{n} \int_{- h + (n - 0,5) Δ}^{- h + (n + 0,5) Δ} \frac{\exp [- j k R (- h + m Δ, ξ)]}{R (- h + m Δ, ξ)} d ξ

( 4.1A.15b )

a do krajů segmentů u potenciálu skalárního

φ [- h + (m + 0,5) Δ] \approx \frac{1}{4 π ε} \sum_{n = 1}^{N} σ_{n^{+}} \int_{- h + n Δ}^{- h + (n + 1) Δ} \frac{\exp {- j k R [- h + (m + 0,5) Δ, ξ]}}{R [- h + (m + 0,5) Δ, ξ]} d ξ

( 4.1A.15c )

Ve vztahu (4.1A.15c), σ _n+ = σ [-h+(n+0.5)Δ].

Vztah, (4.1A.15) může být přepsán do kompaktnějšího tvaru

σ_{n^{+}} \approx \frac{- 1}{j ω} [\frac{I_{n + 1} - I_{n}}{Δ}]

( 4.1A.16a )

A_{z} (m) \approx \frac{μ}{4 π} \sum_{n = 1}^{N} I_{n} \int_{Δ_{n}} \frac{\exp [- j k R (m, ξ)]}{R (m, ξ)} d ξ

( 4.1A.16b )

φ (m^{+}) \approx \frac{1}{4 π ε} \sum_{n = 1}^{N} σ_{n^{+}} \int_{Δ_{n^{+}}} \frac{\exp [- j k R (m^{+}, ξ)]}{R (m^{+}, ξ)} d ξ

( 4.1A.16c )

- E_{z}^{i} (m) \approx - j ω A_{z} (m) - \frac{φ (m^{+}) - φ (m^{-})}{Δ}

( 4.1A.16d )

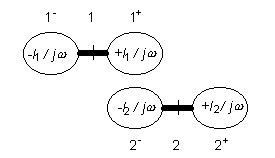
Při odvození (4.1A.16d) byla uvážena okrajová podmínka (4.1A.12e).

Nyní se podrobněji podívejme na rovnici kontinuity (4.1A.16a). Tato podmínka vyjadřuje skutečnost, že jednotlivé segmenty antény mohou být nahrazeny elementárními elektrickými dipóly (obr. 4.1A.5). Uvážíme-li tento fakt, můžeme vyjádřit příspěvek n-tého segmentu (elementárního dipólu) k hodnotě skalárního potenciálu na pravé hranici m-tého segmentu díky (4.1A.16c) jako

φ (m^{+}) = \frac{1}{j ω ε} [I_{n} \int_{Δ_{n^{+}}} \frac{\exp (- j k R)}{4 π R} d ξ - I_{n} \int_{Δ_{n^{-}}} \frac{\exp (- j k R)}{4 π R} d ξ] \frac{1}{Δ}

( 4.1A.17 )

Dosazením (4.1A.17) a (4.1A.16b) do (4.1A.16d) a vynásobením obou stran rovnice délkou segmentu Δ dostáváme

E_{z}^{i} Δ = Z I

( 4.1A.18 )

Pro prvky Z_mn impedanční matice Z platí:

Z_{m n} = j ω μ Δ \int_{Δ_{n}} \frac{\exp [- j k R (m, ξ)]}{4 π R (m, ξ)} d ξ +

+ \frac{1}{j ω ε} [\int_{Δ_{n^{+}}} \frac{\exp [- j k R (m^{+}, ξ)]}{4 π R (m^{+}, ξ)} d ξ - \int_{Δ_{n^{-}}} \frac{\exp [- j k R (m^{+}, ξ)]}{4 π R (m^{+}, ξ)} d ξ] \frac{1}{Δ} -

- \frac{1}{j ω ε} [\int_{Δ_{n^{+}}} \frac{\exp [- j k R (m^{-}, ξ)]}{4 π R (m^{-}, ξ)} d ξ - \int_{Δ_{n^{-}}} \frac{\exp [- j k R (m^{-}, ξ)]}{4 π R (m^{-}, ξ)} d ξ] \frac{1}{Δ}

( 4.1A.19 )

Obr. 4.1A.5

Anténa jako soubor elementárních elektrických dipólů

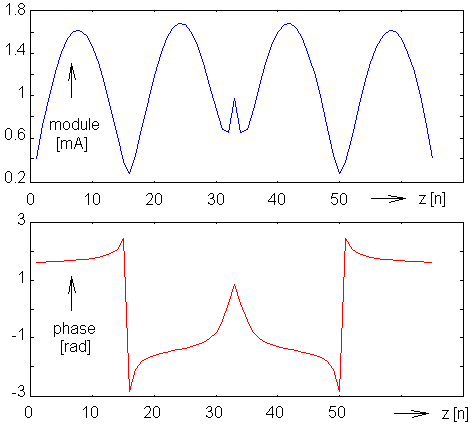
Z_mn popisuje příspěvek proudu a náboje na segmentu n k napětí indukovanému na segmentu m.

Jelikož složka elektrické intenzity, tečná k anténnímu vodiči, je nulová na všech segmentech vyjma napájecí štěrbiny, prvky sloupcového vektoru napětí (levá strana rovnice 4.1A.18) jsou nulové vyjma případu napájecí štěrbiny (na štěrbince jsme předpokládali napětí 1 V). Z rovnice (4.1A.18) tedy můžeme vyjádřit sloupcový vektor uzlových hodnot rozložení proudu na anténě I. Poměr vstupního napětí a vstupního proudu je potom roven vstupní impedanci antény.

Jako příklad si uveďme výsledek analýzy symetrického dipólu s délkou ramene h = λ a s poloměrem anténního vodiče a = 0.001588 λ . Rozložení proudu na anténě, získané pomocí popsané metody, je nakresleno na obr. 4.1A.6.

Ve vrstvě C uvádíme uživatelský popis programu, s jehož pomocí je možno dosáhnout uvedeného výsledku. Ve vrstvě D pak čtenář nalezne informace o tom, jak je možno program efektivně sestavit v Matlabu.

Obr. 4.1A.6

Rozložení proudu na symetrickém dipólu. Po částech konstantní aproximace, Diracovo vážení. Délka dipólu 2λ, průměr 0,001588λ, 64 segmentů.