4.1 Wire dipole

Advanced theory

In dit hoofdstuk introduceren we de lezer in de moment-methode berekening van parameters van een wiredipole. We presenteren deze informatie in het Nederlands in laag B zodat de lezer vertrouwd kan geraken met de Nederlandse termen die gebruikt worden bij antennes. De Engelse vertaling van dit hoofdstuk vindt men in laag A.

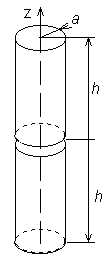
Fig. 4.1B.1

Wire dipole

De technische parameters van antennes (versterking, ingangsimpedantie, derectivity pattern) kunnen berekend worden als de current distribution van het antennedraagvlak gekend is. Spijtig genoeg geeft de berekening van current distribution problemen omdat er integraal vergelijkingen moeten worden opgelost.

Er zijn 2 basisbenaderingen voor het oplossen van integraalvergelijkingen. Deze zijn interatieve en momentopnames. Interative methodes zijn gebaseerd op de ruwe benadering van de current distribution (v.b. sinus) waardoor deze zo nauwkeuriger wordt gemaakt. Anderzijds, moment methodes vormen de integraal vergelijkingen om tot een set van parallelle lineaire vergelijkingen, welke opgelost kunnen worden door matrix bewerkingen.

In dit hoofdstuk gaat onze aandacht vooral naar het moment analyse van draadantennes. In alle gevallen worden de antennes verondersteld om cirkelvormige cilinders te zijn met een straal a en een lengte = 2h. De as van de antenne wordt voorgesteld door de z-as (fig. 4.1B.1) van het cilindervormig coördinaten systeem (r, ρ, z). De antenne wordt in een vacuüm omgeving geplaatst (μ = μ₀, ε = ε₀, σ = 0) en er worden geen verliezen verondersteld.

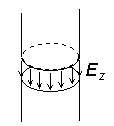
Fig. 4.1B.2

Exciting electrical field between dipole terminals

In het centrum van de cilinder (z=0), is er een korte opening. In deze opening veronderstellen we een harmonische generator welke een symmetrisch elektrisch veld genereert (fig. 4.1B.2). De spanning wordt verondersteld

V = - \int_{g a p} E_{z} d z

( 4.1B.1 )

hier 1V te bedragen. In (4.1.B.1) is E_z de z-component van de elektrische veldintensiteit van de antenne oppervlakte (fig. 4.1B.2). Buiten het gat, E_z is nul omwille van de perfecte geleiding van de cilinder.

I. Moment methode

Laten we een algemene integraalvergelijking nemen.

\int_{a}^{b} f (z, ξ) d ξ = g (z)

( 4.1B.2 )

In deze formule is f een niet gekende functie, <a,b> is het interval en g is een gekende functie die wordt voorgesteld door de bron. De moment oplossing van (4.1.B.2) kan men bekomen in 3 stappen:

De ongekende functie f kan men herschrijven door een lineaire combinatie van een gekende basisfunctie f_n en een ongekende coëfficiënt c_n.
$f \approx \tilde{f} = \sum_{n = 1}^{N} c_{n} f_{n}$ . ( 4.1B.3 )
De benadering van de ongekende functie f^~ is terug vervangen door de opgeloste vergelijking (4.1B.2). Hier zijn de sommatie en de integratie verwisseld. Dit bekomt
$\sum_{n = 1}^{N} c_{n} \int_{a}^{b} f_{n} (z, ξ) d ξ = g (z) + R (z)$ . ( 4.1B.4 )
Hier is, R(z) het residuum welk het feit uitdrukt dat de benadering f^~ niet helemaal overeen komt met (4.1B.2). De vergelijking (4.1B.4) is een vergelijking voor N aantal ongekende coëfficienten c_n.
De benadering f^~ is zo nauwkeurig mogelijk als het residuum R minimaal is. Vandaar dat het residuum geminimaliseerd wordt door de weighted residua methode : Het produkt van een weegfunctie w en het residuum R geintegreerd over het interval <a, b> moet nul zijn [5]. Als N aantal weegfuncties worden gebruikt, dan is de set van N aantal gelijkaardige lineaire vergelijkingen voor N aantal ongekende coëfficienten c_n gegeven in
$\int_{a}^{b} w_{m} (z) R (z) d z = 0 m = 0,1,... N$ , ( 4.1B.5a )

$\sum_{n = 1}^{N} c_{n} \int_{a}^{b} w_{m} (z) \int_{a}^{b} f_{n} (z, ξ) d ξ d z = \int_{a}^{b} w_{m} (z) g (z) d z$ . ( 4.1B.5b )
Beide basis functies en weegfuncties moeten lineair onafhankelijk zijn van het interval <a,b>.

II. Basis Functies

Basis functies kunnen globaal of locaal zijn. Globale basis functies worden afgebakend op het hele gebied <a,b>. V.b., systeemfuncties

f_{n} (z) = \cos (\frac{π n z}{h})

( 4.1B.6 )

Fig. 4.1B.3

Multi-basis approximations a) piece-wise constant, b) piece-wise linear

zijn op <a,b> lineair onafhankelijk en de coëfficienten c_n in volgende benadering

f (z) \approx \tilde{f} (z) = \sum_{n = 1}^{N} c_{n} f_{n} = \sum_{n = 1}^{N} c_{n} \cos (\frac{π n z}{h})

( 4.1B.7 )

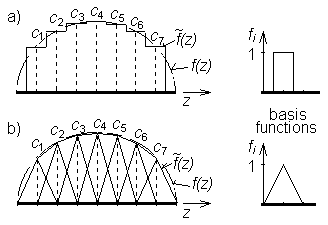
hebben dan betekenis op de Fourier coëfficienten van de stroomdichtheids verdeling.

Deze benadering gebaseerd op de globale basis functies noemt men de single-basis benadering.

Locale basis functies worden ook afgebakend op het hele gebied, maar elk van hen is niet gelijk aan nul voor de deelgebieden van het interval <a,b> zoals men kan zien in fig. 4.1B.3. Als basis functies worden genormaliseerd, dan hebben de coëfficienten c_n de betekenis van knoopwaardes van de berekende functie f (fig. 4.1B.3). Benadering gebaseerd op de locale basis functies noemt men multi-basis benaderingen.

III. Weeg functies

Punt matching en Galerkins methodes zijn de meest algemene vormen van residuum minimalisatie.

Punt matching (of rangregeling) maken gebruik van Dirac pulsen, welke geplaatst worden op plaatsen waar men de ongekende waarde van de stroom distributie wil berekenen, zoals weeg functies

w_{m} (z) = δ (z - z_{m})

( 4.1B.8 )

Punt matching methodes vereisen zeer weinig berekeningen omdat onze integratie geëlimineerd wordt in (4.1B.5b) dankzij de filtering van de Dirac pulsen

\sum_{n = 1}^{N} c_{n} \int_{a}^{b} f_{n} (z_{m}, ξ) d ξ = g (z_{m})

( 4.1B.9 )

Aan de andere kant is de minimalisatie van het residuum enkel verwant tot de matching points z_m.

In de Galerkins methode zijn weeg functies identiek aan basis functies

w_{m} (z) = f_{m} (z)

( 4.1B.10 )

Galerkins methode vertoont meer beredeneringen in vergelijking met de matching point methode omdat een van de integraties niet kan worden weggewerkt. Anderzijds is de residuum minimalisatie hier voorgesteld voor elk punt z ∈ <a,b>.

IV. Draad antennes

Veronderstel de cylindervormige antenne van fig. 4.1B.1. Dan kan het uitgestraalde elektromagnetische veld uitgedrukt worden in een vectorpotentiaal A en scalair potentiaal φ. Deze moeten overeenkomen met niet-homogene golfvergelijkingen [2]

\frac{\partial^{2} A_{z} (z)}{\partial z^{2}} + k^{2} A_{z} (z) = - μ_{0} J_{z} (z)

( 4.1B.11a )

\frac{\partial^{2} φ (z)}{\partial z^{2}} + k^{2} φ (z) = - \frac{ρ (z)}{ε_{0}}

( 4.1B.11b )

Hier is J_z de z-component van de stroomdichtheid [A.m^-2] opgewekt door de bron in de antenne. ρ is het volume van de ladingsdichtheid [C.m^-3] in de antenne, A_z is de z-component van het vector potentiaal en φ is het scalair potentiaal, k=2π/λ is het golfaantal en λ is de golflengte.

De stroom die vloeit in de antenne veroorzaakt een spanningsophoping in de cilinder. Dit verschijnsel noemt men de continuiteitsvergelijking van de regressievergelijking [2]

\frac{\partial J_{z} (z)}{\partial z} + j ω ρ (z) = 0

( 4.1B.12a )

Als de straal van de antenne-cilinder veel kleiner is dan de golflengte a << λ dan mag men veronderstellen dat de stroom zich concentreerd in de as van de cilinder [5], en door het oplossen van (4.1B.11) bekomt men [2]

A_{z} (z) = \frac{μ}{4 π} \int_{2 h} I_{z} (ξ) \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1B.12b )

φ (z) = \frac{1}{4 π ε} \int_{2 h} σ (ξ) \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1B.12c )

Hier is I_z(ξ) de stroom [A] die vloeit in de as van de cilinder, σ(ξ) is de ladingsdichtheid [C.m^-1] in de as van de cilinder, R(z,ξ) is de afstand tussen de plaats ξ van de elektromagnetische veldbronnen I_z(ξ) en σ(ξ) en de locatie z potentiëlen A(z) en φ(z).

Op basis van A(z) en φ(z), kan de elektrische intensiteit van de veldstralen van de antenne berekend worden [2]

E_{z}^{s} (z) = - j ω A_{z} (z) - \frac{\partial φ (z)}{\partial z}

( 4.1B.12d )

De elektrische intensiteit moet hier gelijk zijn aan de grenswaarde van het antennedraagvlak S

E_{z}^{i} + E_{z}^{s} = 0

on S

( 4.1B.12e )

Eⁱ_z veronderstelt hier de elektrische intensiteit van de golf. In het geval van een gebruikelijke antenne is Eⁱ_z de intensiteit van de voedingsbron (op het antennedraagvlak). V.b. de intensiteit in het gat (fig. 4.1B.2).

Als men de stroomdistributie van de antenne wil berekenen, dan zal men eerste de set van vergelijkingen (4.1B.12) moeten uitwerken.

Als men de grensvoorwaarden wil bereiken (4.1B.12e) zal men de elektrische intensiteit moeten berekenen op het draagvlak van de draad. Dit is waarom de afstand R beschreven staat als volgt

R (z, ξ) = \sqrt{a^{2} + {(z - ξ)}^{2}}

( 4.1B.13 )

In de volgende paragrafen worden constante basis functies, en Dirac weeg functies stapsgewijs gebruikt voor het uitwerken van (4.1B.12).

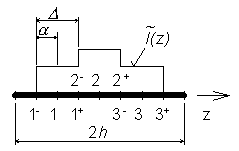
Fig. 4.1B.4

Piece-wise constant approximation

In de eerste stap wordt de geanalyseerde structuur gediscritiseerd. Opsplitsing van antenne is vertoont in fig. 4.1B.4. Lagere delen worden voorgesteld door een ”-”, hogere delen door een ”+”. Lagere delen van het eerste segment en hogere delen van het laatste segment zijn weggelaten van het einde van de antenne om zo de conditie I(-h)=I(h)=0 te bereiken. De segmentlengtes zijn Δ = 2α.

Het stapsgewijs vervangen van constante benaderingen naar de integraal vergelijking (4.1B.12b,c) bekomt

A_{z} (z) \approx \frac{μ}{4 π} \sum_{n = 1}^{N} I_{n} \int_{- h + (n - 0,5) Δ}^{- h + (n + 0,5) Δ} \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1B.14b )

φ (z) \approx \frac{1}{4 π ε} \sum_{n = 1}^{N} σ_{n} \int_{- h + (n - 0,5) Δ}^{- h + (n + 0,5) Δ} \frac{\exp [- j k R (z, ξ)]}{R (z, ξ)} d ξ

( 4.1B.14c )

I_n en σ_n zijn knoopwaardes van de stroomladings dichtheid distributie.

Omdat de eerste afleiding van de stapsgewijze constante benadering nul is voor de constante secties en niet bestaat in de grensgevallen, zijn (4.1B.12a) en (4.1B.12d) herschreven in termen van eindige verschillen. In het geval dat I_n = I_z(-h+nΔ) wordt dan verondersteld dat de continuiteitsvergelijking als volgt kan worden uitgedrukt

\frac{I_{z} (- h + (n + 1) Δ) - I_{z} (- h + n Δ)}{Δ} + j ω σ (- h + (n + 0,5) Δ) \approx 0

( 4.1B.15a )

en de relatie voor het berekenen van elektrische intensiteit is dan van de vorm

E_{z}^{s} (- h + n Δ) \approx - j ω A_{z} (- h + n Δ) - \frac{φ [- h + (n + 0,5) Δ] - φ [- h + (n - 0,5) Δ]}{Δ}

( 4.1B.15d )

De relaties (4.1B.15a) en (4.1B.15d) tonen on dat de Dirac pulsen voor punt matching in het centrum van de segmenten worden geplaatst voor het vector potentiaal

A_{z} (- h + m Δ) \approx \frac{μ}{4 π} \sum_{n = 1}^{N} I_{n} \int_{- h + (n - 0,5) Δ}^{- h + (n + 0,5) Δ} \frac{\exp [- j k R (- h + m Δ, ξ)]}{R (- h + m Δ, ξ)} d ξ

( 4.1B.15b )

en de grensen van de segmenten voor het scalair potentiaal

φ [- h + (m + 0,5) Δ] \approx \frac{1}{4 π ε} \sum_{n = 1}^{N} σ_{n^{+}} \int_{- h + n Δ}^{- h + (n + 1) Δ} \frac{\exp {- j k R [- h + (m + 0,5) Δ, ξ]}}{R [- h + (m + 0,5) Δ, ξ]} d ξ

( 4.1B.15c )

In (4.1B.15c), σ_n+ = σ [-h+(n+0.5)Δ].

(4.1B.15) kan men herschrijven in een compactere vorm

σ_{n^{+}} \approx \frac{- 1}{j ω} [\frac{I_{n + 1} - I_{n}}{Δ}]

( 4.1B.16a )

A_{z} (m) \approx \frac{μ}{4 π} \sum_{n = 1}^{N} I_{n} \int_{Δ_{n}} \frac{\exp [- j k R (m, ξ)]}{R (m, ξ)} d ξ

( 4.1B.16b )

φ (m^{+}) \approx \frac{1}{4 π ε} \sum_{n = 1}^{N} σ_{n^{+}} \int_{Δ_{n^{+}}} \frac{\exp [- j k R (m^{+}, ξ)]}{R (m^{+}, ξ)} d ξ

( 4.1B.16c )

- E_{z}^{i} (m) \approx - j ω A_{z} (m) - \frac{φ (m^{+}) - φ (m^{-})}{Δ}

( 4.1B.16d )

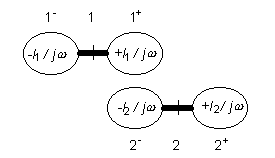
In (4.1B.16d), is de randvoorwaarde (4.1B.12e) opgenomen.

Laten we nu een kijkje nemen op de continuiteitsvergelijking (4.1B.16a); het drukt het feit uit dat genmenten van de antenne vervangen kunnen worden door elementaire elektrische dipolen (fig. 4.1B.5). Dit in gedachten genomen, productie van het n^th segment van het scalair potentiaal kan berekend worden op basis van (4.1B.16c)

φ (m^{+}) = \frac{1}{j ω ε} [I_{n} \int_{Δ_{n^{+}}} \frac{\exp (- j k R)}{4 π R} d ξ - I_{n} \int_{Δ_{n^{-}}} \frac{\exp (- j k R)}{4 π R} d ξ] \frac{1}{Δ}

( 4.1B.17 )

Vervangen we (4.1B.17) en (4.1B.16b) in (4.1B.16d) en multiplexen we beide kanten door Δ dan bekomen we

E_{z}^{i} Δ = Z I

( 4.1B.18 )

waar

Z_{m n} = j ω μ Δ \int_{Δ_{n}} \frac{\exp [- j k R (m, ξ)]}{4 π R (m, ξ)} d ξ +

+ \frac{1}{j ω ε} [\int_{Δ_{n^{+}}} \frac{\exp [- j k R (m^{+}, ξ)]}{4 π R (m^{+}, ξ)} d ξ - \int_{Δ_{n^{-}}} \frac{\exp [- j k R (m^{+}, ξ)]}{4 π R (m^{+}, ξ)} d ξ] \frac{1}{Δ} -

- \frac{1}{j ω ε} [\int_{Δ_{n^{+}}} \frac{\exp [- j k R (m^{-}, ξ)]}{4 π R (m^{-}, ξ)} d ξ - \int_{Δ_{n^{-}}} \frac{\exp [- j k R (m^{-}, ξ)]}{4 π R (m^{-}, ξ)} d ξ] \frac{1}{Δ}

( 4.1B.19 )

Fig. 4.1B.5

Antenna as a set of elementary electrical dipoles

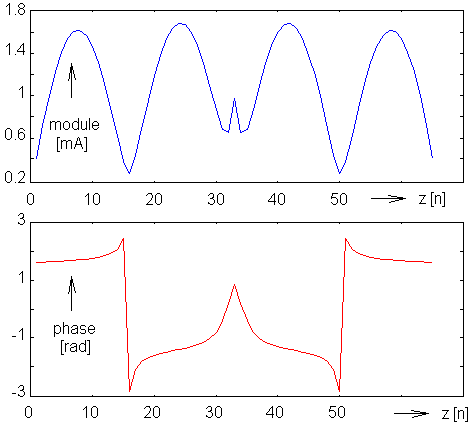
de stroomlading op het n^th segment voorgesteld tot de spanning opgewekt in het m^th segment.

Omdat de elektrische intensiteit nul is voor alle segmenten behalve het voedingsgat, de elementen van de spanningsvector bedragen nul behalve voor het gatsegment dat gelijk is aan 1. (4.1B.18) voorziet de stroomdistributie I. De verhouding van de ingangsspanning en de ingangsstroom geeft dan de ingangsimpedantie van de geanalyseerde antenne.

Een voorbeeld van de resultaten van de analyse is voorgesteld in fig. 4.1B.6; module en fase van de stroomdichtheidsverdeling van de dipool h = λ en a = 0.001588 λ is daar bekomen.

Men kan meer informatie vinden over de bekomen resultaten (fig. 4.1B.6) door middel van een computer programma. Dit programma is voorgesteld in laag C. In laag D is het programma uitgelegd door de programmeur.

Fig. 4.1B.6

Current distribution on the symetrical dipole. Piece-wise constant approximation, point matching. Length of dipole 2λ, diameter 0.001588λ, number of segments 64.