4.2 Mutual impedanceBasic theoryRadiating elements (dipoles, loops, etc.) are usually grouped into an antenna array and fed from a common source in order to primarily reach the desired directivity pattern of the radiation. Designing the feeding system of an antenna array, even the mutual influence among the antenna elements has to be considered and a true value of the impedance at the input of each antenna element has to be determined. Knowledge of these entries enables to determine input current of each antenna element and even currents on the feeding ports of the array. Moreover, the structure of the feeding system can be modified to reach a suitable value of the input impedance of the antenna array in its whole. In this chapter, we concentrate on the method of calculating input impedance of a linear antenna (dipole) by the method of induced electromotoric forces. The approach is then going to be generalized in order to compute impedances of single elements in the antenna array. Radiation impedance ZΣ of the antenna can be considered as a proportionality constant between the complex power PΣ, which is radiated by the antenna, and the squared value of the related current I
As a related current, we consider the input current of the element Ivst or the value of the current Im in the maximum of the standing wave. Since currents Ivst and Im of the same antenna (under identical conditions) usually differ, but the radiated power stays the same, even the values of the radiation impedance differ - the value of ZΣvst related to the input current Ivst and the value of ZΣm related to the current in its maximum Im are not the same. Neglecting losses of the antenna, the radiation impedance ZΣvst equals to the input impedance of the antenna Zvst computed as a ratio of input voltage Uvst and input current Ivst
The above-defined values of input impedance Zvst are usually provided for basic types of antennas. These values are valid for antennas placed in free space, i.e. in satisfactorily long distance from other antennas or objects. A detailed algorithm of computing Zvst, which is based on the radiated power, is given in the layer B. In an antenna array, single antenna elements mutually influence themselves and impedance of each element depends on the type of elements in the surrounding, on the way of their positioning and feeding. In order to evaluate and compute the mutual influence, we change our view to the equation (4.2A.2). The current I is assumed to be excited in the antenna any way. The current I is characterized by the current Ivst and by a function of current distribution. Antenna radiates and creates a given intensity of electric field E in its surrounding, which is proportional to the current on the antenna. A certain field intensity Et appear even on the surface of the radiating antenna. At the same moment, antenna acts as the receiving antenna, and the receive results in a given voltage at the input port of the antenna. Voltage Uvst in eqn. (4.2A.2) can be therefore considered as a voltage, produced on the antenna by the receive of the own radiation. This own radiation is proportional to the current magnitude Ivst at its input and the quantity Zvst (self-impedance) plays the role of the proportionality constant. The above-described consideration can be simply applied to the whole antenna array. Even in the array, there is a certain field intensity Et on the surface of each antenna element. This field is not created not only by the self-radiation of the antenna element but too by the radiation of the other elements.
In fig. 4.2A.1, the antenna array consisting of n elements (dipoles), which are fed by currents Ivst i on their input terminals, is depicted. In analogy to (4.2A.2), input voltages of antenna elements are given by the following set of equations
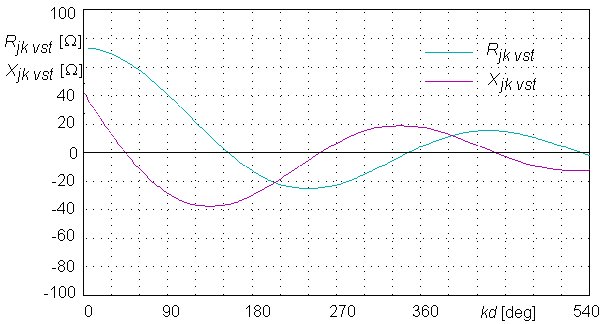
Impedance coefficients Zjk (4.2A.3) express the mutual coupling between j-th and k-th element and are called mutual impedance. Mutual impedance is a complex quantity fulfilling Zjk= Zkj. Its magnitude depends on the shape, on the dimensions and on the mutual position of antenna elements, and even on their current distribution. Coefficient Zjj is called self-impedance and determines relation between the current and the voltage at the input of antenna elements out of the array and equals to the radiation impedance of a separated j-th antenna element in free space. Typical dependency of the components of the mutual impedance Zjk = Rjk+ jXjk on the distance d (multiplied by wave-number k = 2π/λ) between two parallel dipoles of the same length is depicted in fig. 4.2A.2.
Magnitude of mutual impedance depends on dimensions and on the distance of antenna elements. Real and imaginary component of mutual impedance can be both positive and negative and its maximum values decrease when the distance between elements d rises (the influence of very distant elements negligible).
Values of mutual impedance, which are provided for technical needs in charts, are usually related to the current in maximum. Re-computation to input terminals can be done considering the sine current distribution on the antenna
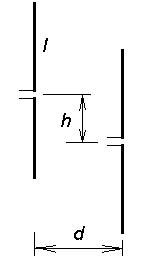
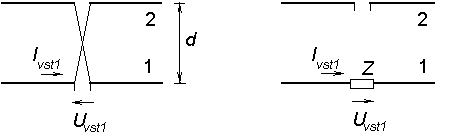
where kl = (2π/λ) l, if antenna length l is not close to the integral multiple of λ/2. More accurate values of mutual impedance can be computed using the program from the layer C. The program computes values of mutual impedance Zjk, related to the maximum current or to the input one for a couple of two parallel dipoles of the same length and of the same standing wave on the wire of the dipoles. The length of the dipole l, the distance between dipoles d and the magnitude of the axial shift of the feeding ports of the dipoles h (fig. 4.2A.3) have to be entered when multiplied by wave-number k = 2π/λ. Graphic representation of the magnitude of both components of mutual impedance Rjk and Xjk on the variation of a elected quantity (l, d or h) is suitable when the influence of the spatial arrangements of the antenna array to the impedance relations is investigated. The same way, components of the radiation impedance Zii at the input of an isolated antenna element can be computed if the distance between elements d is put to be equal to the radius of the antenna wire a. Computing voltages and currents in the system of n antenna elements, 2n independent quantities (n voltages and n currents) have to be determined. Considering the way of feeding, other (n-1) equations can be built. For elected magnitude of a single voltage (current), the (2n-1) unknown quantities can be computed. In antenna arrays, where single antenna elements are fed by the system of transmission lines, computations are complicated by the fact that impedance of each element depends on currents in other elements. That way, relations on transmission lines and radiators are mutually coupled. In case of single fed element, computations are rather simple. Deriving equations (4.2A.3) for a given situation, we have to respect the fact that orientation of voltage Uvst i and of a current Ivst i correspond to the feeding of an element by a generator. In case of a passive element (voltage on the input port is caused by the current Ivst flowing through the load Z of the input port) is the orientation of the voltage opposite, and therefore, the sign has to be changed in (4.2A.3). For two typical situations, corresponding sets of equations are given in fig. 4.2A.4.
Set (4.2A.3) enables to compute the ratio between any couple of unknown quantities. Input impedance of i-th element Zvst i is obtained when dividing i-th eqn. (4.2A.3) by input current of i-th element Ivst i
Impedance of every element of an antenna array is therefore given by the sum of its own impedance Zii and of submissions of the other elements, depending on the product of mutual impedances Zjk and respective currents (amplitudes and phases) flowing through the input ports of those elements. The change of feeding any antenna element therefore causes the change of impedances of all the antenna elements in the array. As an example, let us consider results obtained for the arrays depicted in fig. 4.2A.4. In the case of the couple of dipoles fed by the crossed transmission line of the length d = λ/2 (fig. 4.2A.4a), currents of the same magnitude and the same phase flow in both the dipoles, and both of the dipoles are of the input impedance
Impedance on the port of the dipole "1" equals to the half of the value Zvst1. For the couple of the half-wavelength-long dipoles (kl = 90°), we ge Z11 = (73,1 + j42,5) Ω and Z12 = (-12,5 + j30) Ω. Assuming in-phase feeding (fig. 4.2A.4a), the resultant value of the impedance of both the dipoles equals to Z1 = (60,6 + j12,5) Ω. Considering anti-phase feeding, the resultant input impedance equals to the difference of Z11 and Z12, which yields the result Z1 = (85,6 + j72,5) Ω. The same result is obtained for the dipole in the distance λ/4 from the planar reflector. Impedance on the port "1" in fig. 4.2A.4a equals to the half of the computed value Z1, i.e. Zsoust = (30,3 + j6,2) Ω. Input impedance of the dipole "2" in fig. 4.2A.4b is given by the relation
Substituted values of both the impedances Z11 and Z12 have to be related to the input current of the dipole Ivst in both the cases. | |||||||||||||||||||||||||||||||||||||||||