4.2 Vzájemné impedanceZákladní teorieVyzařující prvky (dipóly, smyčky ap.) jsou obvykle sdružovány do anténní soustavy a napájeny ze společného zdroje především s cílem dosáhnout požadovaného směrového diagramu vyzařování. Při návrhu napájecího systému soustavy antén je třeba postihnout i vzájemné ovlivňování mezi prvky soustavy a určit skutečnou hodnotu impedance na vstupu každého prvku soustavy. Znalost těchto údajů umožní určit vstupní proudy každého prvku i proudy na napájecích svorkách soustavy, ale také modifikovat uspořádání napájecího systému tak, aby bylo dosaženo vhodné velikosti vstupní impedance anténní soustavy jako celku. V této kapitole nejprve se zaměříme na způsob výpočtu vstupní impedance lineární antény (dipólu) metodou indukovaných elektromotorických napětí. Postup pak snadno rozšíříme tak, aby bylo možno vypočítat impedance jednotlivých prvků v anténní soustavě. Impedanci záření ZΣ antény můžeme považovat za konstantu úměrnosti mezi komplexním výkonem PΣ, který anténa vyzařuje, a kvadrátem vztažného proudu I
Vztažným proudem bývá buď vstupní proud prvku Ivst nebo hodnota proudu Im v kmitně stojaté vlny. Protože proudy Ivst a Im na téže anténě (i za stejných podmínek) se většinou liší, ale vyzařovaný výkon je stejný, liší se i hodnoty impedance záření – hodnota ZΣvst vztažená ke vstupnímu proudu Ivst a hodnota ZΣm vztažená k proudu v kmitně Im. U antén se zanedbatelnými ztrátami je impedance záření ZΣvst shodná se vstupní impedancí antény Zvst vypočtenou z poměru napětí Uvst a proudu Ivst na vstupních svorkách prvku
Takto definované hodnoty vstupní impedance Zvst jsou zpravidla udávány pro základní typy antén. Jsou to hodnoty platné pro antény umístěné ve volném prostoru, tedy relativně vzdálené od jiných antén či objektů. Konkrétní postup při výpočtu impedance Zvst, využívající vyzařovaného výkonu, je uveden ve vrstvě B. V anténní soustavě se jednotlivé prvky antény (prvky soustavy) navzájem ovlivňují a impedance každého z nich závisí na tom, jaké prvky jsou v okolí a jak jsou tyto prvky rozmístěné a buzené. Abychom mohli vzájemný vliv posoudit a vypočítat, pozměníme si nejprve náš pohled na rovnici (4.2A.2). Předpokládejme, že v anténě byl nějakým způsobem vybuzen proud I. Ten je charakterizován proudem Ivst a nějakou funkcí proudové distribuce. Anténa září a všude ve svém okolí vytváří jistou intenzitu elektrického pole E, která je (mimo jiné) úměrná proudu v anténě. Jistá intenzita pole Et vznikne i na povrchu samotné antény. Anténa tak současně funguje jako anténa přijímací (nedokáže totiž rozlišit, zda na ni dopadá cizí nebo její vlastní záření) a výsledkem příjmu je pak jisté napětí na vstupních svorkách antény. Napětí Uvst v rovnici (4.2A.2) tedy můžeme považovat za napětí, vzniklé na anténě příjmem vlastního záření. To je úměrné velikosti proudu Ivst na jejím vstupu a konstantou úměrnosti je veličina Zvst (činitel vlastní vazby, vlastní impedance). Je snadné rozšířit předchozí úvahu na anténní soustavu. V soustavě také existuje na povrchu každého prvku nějaká intenzita pole Et. K ní ovšem přispívá nejen vlastní záření tohoto prvku, ale i záření všech ostatních prvků.
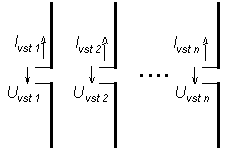
Na obr. 4.2A.1 je nakreslena soustava n prvků (dipólů), buzených proudy Ivst i na jejich vstupních svorkách. V analogii s (4.2A.2) jsou tedy vstupní napětí jednotlivých prvků určena následující soustavou rovnic
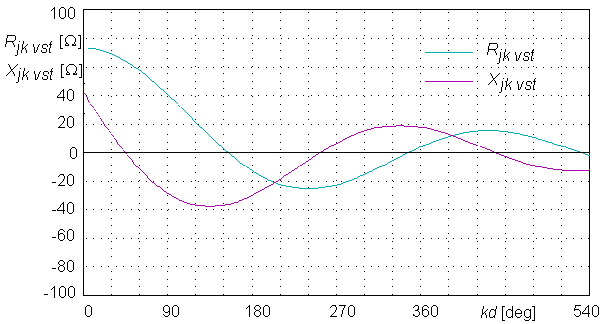
Impedanční koeficienty Zjk vyjadřují vzájemnou vazbu mezi j-tým a k-tým prvkem a bývají nazývány činitelé vazby nebo vzájemné impedance. Činitelé vazby jsou komplexní veličiny a platí, že Zjk = Zkj. Jejich číselné hodnoty závisí na tvaru, rozměrech a vzájemné poloze těchto prvků a také na rozložení proudu na nich. Koeficient Zjj je činitelem vlastní vazby (vlastní impedancí), určuje vztah proudu a napětí na vstupu prvku umístěného mimo soustavu a je roven impedanci záření osamoceného j-tého prvku ve volném prostoru. Typický průběh závislosti složek činitelů vzájemné vazby Zjk = Rjk + jXjk na vzdálenosti d (zadané v součinu s vlnovým číslem k = 2 π/λ) mezi dvěma rovnoběžnými dipóly stejné délky je zobrazen na obr. 4.2A.2.
Hodnoty činitelů vazby závisí dosti složitým způsobem na rozměrech a vzdálenosti prvků. Reálná i imaginární složka činitele vazby nabývá kladných i záporných hodnot a jejich největší hodnoty se zmenšují při zvětšování vzdálenosti d mezi prvky, takže vliv velmi vzdálených prvků (několik vlnových délek) je pak malý.
Hodnoty činitelů vazby, uváděné pro technickou potřebu v grafech, jsou často vztaženy ke kmitně proudu. Přepočet na vstupní svorky je možno provést pomocí sinusové funkce pro rozložení proudu na anténě
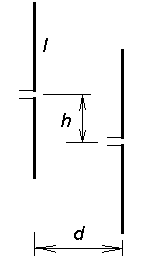
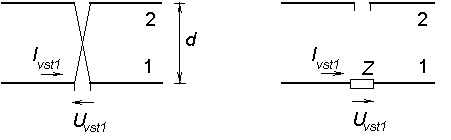
kde kl = (2π /λ) l , pokud délka antény l není blízká k celistvým násobkům λ/2. Přesnější hodnoty činitelů vazby je možno získat využitím výpočetního programu, dostupného ve vrstvě C. Ten poskytuje hodnoty činitelů vzájemné vazby Zjk, vztažené ke kmitně nebo ke vstupu pro dvojici rovnoběžných dipólů se stejnou délkou ramen a se stojatou proudovou vlnou na vodičích dipólů. Délka ramene dipólu l, vzdálenost mezi dipóly d a velikost osového posuvu napájecích svorek dipólů h (obr. 4.2A.3) se zadávají v součinu s vlnovým číslem k = 2π/λ. Grafické vyjádření závislosti velikostí obou složek činitelů vzájemné vazby Rjk a Xjk na změnách zvolené veličiny (l, d nebo h) je vý hodné při sledování vlivu změn prostorového uspořádání anténní soustavy na impedanční poměry na jejích prvcích. Stejným způsobem je možno získat i hodnoty složek impedance záření Zii na vstupu osamoceně umístěného prvku, zadáme-li vzdálenost mezi prvky d rovnou poloměru a vodiče prvku. Při výpočtu napěťových a proudových poměrů v soustavě n prvků je třeba určit 2n nezávislých veličin (n proudů a n napětí). Podle způsobu buzení je možno sestavit ještě dalších (n-1) rovnic odpovídajících danému uspořádání napájecího systému a pro zvolenou velikost jednoho napětí nebo proudu pak vypočítat zbylých (2n-1) neznámých veličin. U anténních soustav, kde jsou jednotlivé prvky buzeny soustavou vedení, komplikuje výpočet proudů skutečnost, že impedance každého prvku závisí také na proudech v ostatních prvcích. Tím jsou poměry na vedení a na zářičích vzájemně vázány. Poměrně jednoduchý bývá výpočet v soustavách s jedním napájeným prvkem – soustava s reflektorem (rovinným, úhlovým) nebo s pasivními prvky (anténa Yagi a pod.). Při sestavování rovnic (4.2A.3) pro konkrétní situaci je třeba respektovat skutečnost, že směr napětí Uvst i a proudu Ivst i odpovídá napájení prvku generátorem. V případě pasivního prvku, u kterého je napětí na vstupních svorkách vyvoláno proudem Ivst tekoucím zátěží Z mezi jeho vstupními svorkami, je smysl napětí opačný, a tomu odpovídá i změna znaménka v (4.2A.3). Pro dvě typické situace jsou odpovídající soustavy rovnic uvedeny v obr. 4.2A.4.
Soustava rovnic (4.2A.3) umožňuje také výpočet poměru mezi kteroukoliv dvojicí neznámých veličin. Vstupní impedanci i-tého prvku Zvst i pak získáme vydělením i-té rovnice (4.2A.3) vstupním proudem i-tého prvku Ivst i
Impedance každého prvku anténní soustavy je tedy dána součtem jeho vlastní impedance Zii a příspěvků od ostatních prvků, závislých na součinu činitelů vazby Zjk a odpovídajících proudů (amplitud i fází) tekoucích vstupními svorkami těchto prvků. Změna buzení některého z prvků anténní soustavy tedy vyvolá změnu impedancí všech prvků soustavy antén. Jako příklad uveďme výsledky získané pro soustavy podle obr. 4.2A.4. U dvojice dipólů napájených zkříženým vedením délky d = λ/2 (obr. 4.2A.4a) tečou v obou dipólech stejně velké proudy se stejnou fází a každý z dipólů má vstupní impedanci
Impedance na svorkách dipólu "1" pak bude polovinou hodnoty Zvst1. Pro dvojici půlvlnných dipólů (kl = 90°) je Z11 = (73,1 + j42,5) Ω a Z12 = (-12,5 – j30) Ω. Pak při soufázovém buzení (obr. 4.2A.4a) bude výsledná hodnota impedance každého z dipólů rovna Z1 = (60,6 + j12,5) Ω, při protifázovém buzení (nezkřížené vedení mezi dipóly na obr. 4.2A.4a) bude rovna rozdílu hodnot Z11 a Z12 a dostaneme výsledek Z1 = (85,6 + j72,5) Ω. Stejný výsledek bychom dostali pro dipól umístěný ve vzdálenosti λ/4 před rovinnou vodivou plochou (dipól s rovinným reflektorem). Impedance na svorkách dipólu "1" v obr. 4.2A.4a (impedance soustavy) bude polovinou vypočtené hodnoty Z1, tedy Zsoust = (30,3 + j6,2) Ω. Vstupní impedance dipólu "2" na obr. 4.2A.4b bude dána vztahem
Dosazované hodnoty složek obou impedancí Z11 a Z12 musí být v obou případech vztaženy ke vstupnímu proudu Ivst dipólu. | |||||||||||||||||||||||||||||||||||||||||