4.2 Vzájemné impedance

Podrobnější popis

Impedanci záření Z_Σvst na vstupních svorkách antény můžeme získat z hodnoty komplexního výkonu P_Σ vyzařovaného anténou dělením vstupním proudem | I_vst|² antény (vztah 4.2A.1 ve vrstvě A). Všimněme si nyní blíže možností výpočtu vyzařovaného výkonu.

Při vyzařování elektromagnetických vln se energie dodaná bezeztrátové anténě ve volném prostoru transformuje na energii vlny šířící se prostorem, a na energii periodicky vyměňovanou mezi zdrojem a elektromagnetickým polem v blízkém okolí antény. Vyzařovaný výkon P_Σ (obecně komplexní) pak můžeme vypočítat integrací Poyntingova vektoru po uzavřené ploše kolem antény. Získaný výsledek je ovlivněn volbou oblasti, ve které je integrace prováděna.

Ve vzdálené oblasti (zóna záření) jsou intenzity elektrického pole E a magnetického pole H vyzářené elektromagnetické vlny ve fázi. Poyntingův vektor má pouze reálnou složku a jeho integrací po uzavřené ploše (nejčastěji koule se středem na anténě) dostaneme činný výkon P_Σ. Dělením kvadrátem proudu I_vst pak získáme pouze reálnou složku impedance záření R_Σvst.

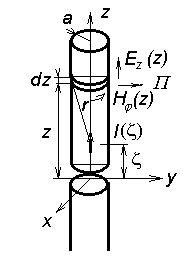
Obr. 4.2B.1

Intenzity polí na povrchu anténního vodiče

Při výpočtu komplexního vyzařovaného výkonu P_Σ je třeba integrovat Poyntingův vektor v bezprostřední blízkosti antény (u lineárních antén přímo po povrchu anténního vodiče). Všimněme si nejprve vyzařování symetrického dipólu s délkou ramene l a průměrem vodiče 2a, který je umístěn do souřadné soustavy podle obr. 4.2B.1. Proud I(z) vytvoří na povrchu válcového vodiče antény podélnou tečnou složku intenzity elektrického pole E_z(z) a příčnou tečnou složku intenzity magnetického pole H_φ(z).

Intenzita magnetického pole H_φ(z) na povrchu nepříliš tlustého vodiče je určena převážně proudem I(z) v nejbližším okolí elementu dz a podle Ampérova zákona je

H_{φ} (z) = \frac{I (z)}{2 π a}

( 4.2B.1 )

Intenzitu elektrického pole E_z(z) na povrchu vodiče antény je možno vyjádřit pomocí vektorového potenciálu A_z(z) využitím známého rozložení proudu I(z)

A_{z} (z) = \frac{μ}{4 π} \int_{- l}^{l} I (ζ) \frac{e^{- j k r}}{r} d ζ

r = \sqrt{{(z - ζ)}^{2} + a^{2}}

( 4.2B.2 )

Intenzita elektrického pole E_z(z) pak bude rovna

E_{z} (z) = - j ω (A_{z} + \frac{1}{k^{2}} g r a d_{z} d i v (A_{z})) = - j ω (A_{z} + \frac{1}{k^{2}} \frac{\partial^{2} A_{z}}{\partial z^{2}})

( 4.2B.3 )

Je-li poloměr vodiče a podstatně menší než jeho délka l a zanedbáme-li vyzařování konců vodiče, má Poyntingův vektor pouze radiální složku

Π = - E_{z} (z) H_{φ}^{*} (z)

( 4.2B.4 )

Element povrchu vodiče dS = 2π a dz vyzáří výkon

d P_{Σ} = Π 2 π a d z = - E_{z} (z) I_{z}^{*} (z) d z

( 4.2B.5 )

kde hvězdičkou je označena komplexně sdružená hodnota.

Komplexní výkon P_Σ vyzářený celou anténou získáme integrací podél obou ramen dipólu

P_{Σ} = \int_{- l}^{l} d P_{Σ} = - \int_{- l}^{l} E_{z} (z) I_{z}^{*} (z) d z

( 4.2B.6 )

Složky impedance záření Z_Σvst na vstupních svorkách dipólu získáme dělením výkonu P_Σ kvadrátem vstupního proudu I_vst

Z_{Σ v s t} = - \frac{1}{{| I_{v s t} |}^{2}} \int_{- l}^{l} E_{z} (z) I_{1}^{*} (z) d z

( 4.2B.7 )

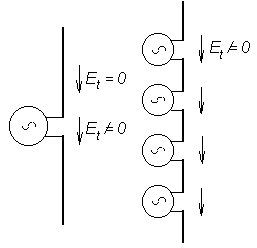
Naznačený výpočet je formálně jednoduchý, ale při konkrétním řešení vznikají potíže při vyčíslení integrálů. Cennou předností naznačeného postupu je však možnost výpočtu impedancí prvků v anténní soustavě, jak bylo uvedeno ve vrstvě A.

Než k tomuto rozšíření přistoupíme, podívejme se ještě na předchozí úvahu přísnějším pohledem. Pozorný čtenář bude totiž protestovat proti orientaci vektoru Π v obr. 4.2B.1, která neodpovídá pravotočivému systému E × H. Kromě toho není jasné, odkud se vzalo znaménko "minus" v rovnici (4.2B.4). Lze sice argumentovat tím, že obrácená orientace a obrácené znaménko se navzájem kompenzují, ale (podle známého přísloví o vlku a koze) naše pochybnost zůstává celá. Navíc se jiný pozorný čtenář naivně jistě zeptá, proč se vlastně dělají antény z dobře vodivých materiálů. Vždyť při nekonečné vodivosti anténního vodiče musí vymizet tečná složka intenzity elektrického pole, hodnota Π bude nulová a tedy taková dokonalá anténa vůbec nevyzařuje. Ten přísnější pohled je tedy vskutku žádoucí.

S tou nulovou tečnou složkou je to téměř pravda. Předpokládejme, že materiál, z něhož je anténní vodič vyroben, je nekonečně vodivý. Pokud při naší úvaze (a výpočtu) vycházíme z přesné funkce rozložení proudu, pak skutečně dostaneme nulovou tečnou složku intenzity na povrchu anténního vodiče. Tedy všude na anténě, s výjimkou velmi krátkého (nekonečně krátkého) úseku v místě z = 0, kde je napájecí štěrbina a kde nekonečně vodivý materiál není. Tečná složka intenzity elektrického pole je tedy na povrchu dokonale vodivé antény všude nulová s výjimkou napájecí štěrbiny. Považujeme-li Poyntingův vektor za plošnou hustotu toku výkonu, zdá se, že anténa vyzařuje jenom v napájecí štěrbině.

Konečná vodivost skutečných materiálů na tomto zjištění nic nemění. Tečná složka sice nulová na povrchu není, ale činný výkon vstupuje dovnitř vodiče, je poměrně malý a je to výkon, který se ve vodiči mění v teplo. Jediné místo, kde reálná složka Poyntingova vektoru směřuje z antény ven, je stále napájecí štěrbina.

Toto zjištění je překvapující a právem může vyvolat pochybnosti. Přinejmenším je však v rozporu s představou antény jako souboru vyzařujících elementárních dipólů. V zápětí však uvidíme, že se s těmito problémy můžeme vyrovnat celkem snadno.

Předně nic nedokazuje, že anténa vyzařuje výkon jen v napájecí štěrbině. Poyntingova věta pouze tvrdí, že integrál součinu E_t(z) H(z) po uzavřené ploše je roven celkovému procházejícímu výkonu. Význam plošné hustoty výkonu tomuto součinu pouze přisuzujeme, protože je to obvykle možné. Rozpor s teorií tu tedy není a otázku, kde se výkon vyzařuje, si nemusíme (a ani nemůžeme) klást a můžeme zůstat u našich dosavadních představ.

Avšak ani z matematického hlediska tu vážné potíže nevzniknou. Z praktických důvodů totiž neprovádíme výpočty s přesnou funkcí proudové distribuce I(z), ale s funkcí přibližnou I'(z) (obvykle sinusovou). Již velmi malý rozdíl mezi funkcemi I(z) a I'(z) stačí, aby tečná složka intenzity elektrického pole na povrchu vodiče se všude lišila od nuly a integrál (4.2B.6) můžeme spočítat. Výpočet je tedy možný s přibližnou funkcí proudové distribuce I'(z). Že je pak i přiměřeně správný, ukážeme podle A. A. Pistolkorse následující úvahou.

Obr. 4.2B.2

Náhrada buzení antény pro rozložení proudu I'(z)

Skutečná anténa (symetrický dipól) je nakreslena na obr. 4.2B.2a. Je z dokonale vodivého materiálu, proud je rozložen podle funkce I(z) a všude na povrchu (s výjimkou napájecí štěrbiny) je tečná složka intenzity elektrického pole nulová. Protože však počítáme s přibližnou funkcí rozložení I'(z), dostáváme E_t různé od nuly a v důsledku toho i určitý vyzařovaný výkon.

Abychom dokázali, že takto vypočítaný výkon je přibližně roven výkonu, který anténa skutečně vyzařuje, mysleme si, že místo skutečné antény řešíme jakousi náhradní anténu, tvarově i rozměrově shodnou, pro kterou je však funkce I'(z) přesnou funkcí rozložení proudu. Má-li tomu tak být, musí být náhradní anténa jinak buzená. Konkrétně musíme připustit buzení souvislou řadou elementárních zdrojů (obr. 4.2B.2b), jejichž napětí jsou nastavena tak, aby se proud rozložil přesně podle funkce I'(z) . U náhradní antény je ovšem správné, že na povrchu není tečná složka intenzity nulová, protože anténa má po celém povrchu rozloženy napájecí štěrbiny. Námi vypočítaný výkon je tedy správně vypočítaný výkon vyzařovaný náhradní anténou. Je-li rozdíl mezi funkcemi I(z) a I'(z) malý, je jistě alespoň přibližně roven výkonu, který vyzařuje anténa skutečná.

Po této diskusi se můžeme vrátit zpět k základní úvaze.

V soustavě rovnoběžných dipólů (obr. 4.2A.1 ve vrstvě A) nejprve vyjádříme výkon vyzářený prvním prvkem soustavy. Výsledná intenzita elektrického pole E_z1(z) na povrchu prvního prvku je rovna součtu příspěvků od všech prvků soustavy

E_{z 1} (z) = E_{11} (z) + E_{12} (z) + \dots \dots + E_{1 n} (z)

( 4.2B.8 )

Výkon P_Σ₁ vyzářený prvním prvkem získáme dosazením do rovnice (4.2B.6). Formální úpravou pak dostaneme vztah

\begin{array}{l} P_{Σ 1} = - \int_{- l}^{l} [E_{11} (z) I_{1}^{*} (z) + E_{12} (z) I_{1}^{*} (z) + \dots \dots + E_{1 n} (z) I_{1}^{*} (z)] d z = \\ = I_{v s t 1}^{*} [- I_{v s t 1} \int_{- l}^{l} \frac{E_{11} (z)}{I_{v s t 1}} \frac{I_{1}^{*} (z)}{I_{1 v s t}^{*}} d z - I_{v s t 2} \int_{- l}^{l} \frac{E_{12} (z)}{I_{v s t 2}} \frac{I_{1}^{*} (z)}{I_{1 v s t}^{*}} d z - \dots \dots - I_{v s t n} \int_{- l}^{l} \frac{E_{1 n} (z)}{I_{v s t n}} \frac{I_{1}^{*} (z)}{I_{1 v s t}^{*}} d z] \end{array}

( 4.2B.9 )

Integrály

Z_{j k} = \int_{- l}^{l} \frac{E_{j k} (z)}{I_{v s t k}} \frac{I_{j}^{*} (z)}{I_{v s t j}^{*}}

( 4.2B.10 )

se nazývají činitelé vazby nebo vzájemné impedance a mají rozměr impedance. Díky provedené formální úpravě jsou integrály (4.2B.10) nezávislé na velikostech proudů v prvcích soustavy, neboť intenzita E_jk vyvolaná na povrchu j-tého prvku zářením proudu v k-tém prvku je úměrná proudu I_{vst k} v k-tém prvku soustavy antén.

Výsledky integrace v (4.2B.10) jsou pro rovnoběžné dipóly vyjádřeny pomocí tabelovaných funkcí (integrální sinus, integrální kosinus). Pro získání číselných hodnot složek činitelů vazby Z_jk je možno s výhodou využít programu, popsaného ve vrstvě C. Výsledky vyjadřují vazbu mezi dvojicí rovnoběžných dipólů se stejnou délkou ramen l, vztažené k proudu v kmitně I_max. Hodnoty Z_{jk vst}, vztažené k proudu na vstupních svorkách dipólu, jsou pak získány přepočtem podle vztahu (4.2A.4) ve vrstvě A.

Závislost velikostí složek činitelů vazby na vzdálenosti mezi dipóly již byla demonstrována ve vrstvě A (obr. 4.2A.2) pro dvojici rovnoběžných symetrických dipólů se stojatou proudovou vlnou. Záporné hodnoty složek činitelů vazby R_jk a X_jk vyjadřují, že při daném prostorovém uspořádání záření k-tého prvku zmenšuje velikost činné nebo jalové složky výkonu P_Σj vyzařovaného j-tým prvkem soustavy. Zmenšování velikostí složek činitelů vazby pro velké vzdálenosti odpovídá poklesu intenzity elektrického pole E_jk se vzrůstající vzdáleností.

Pomocí vztahu (4.2B.10) je možno vypočítat také impedanci osamoceného prvku Z_jj, volíme-li vzdálenost mezi prvky d rovnou poloměru anténního vodiče a. Tento postup zcela odpovídá situaci popsané při odvození rovnice (4.2B.7), kde je uvažována intenzita elektrického pole na povrchu j-tého vodiče E_jj vybuzená proudem tekoucím po ose tohoto vodiče.

V obecnější situaci, kdy na vodičích prvků soustavy je rozložení proudu I(z) vyjádřeno kombinací stojaté vlny a vlny postupné, je možno rovněž postupovat výše uvedeným způsobem při odvození vztahů pro výpočet hodnot činitelů vazby mezi prvky. Vzhledem k výrazně větší složitosti získaných vztahů se však tyto situace řeší výjimečně.

Metoda indukovaných elektromotorických napětí umožňuje výpočet vyzařovaného výkonu a následně i činitelů vzájemné vazby i v situacích, kdy vodiče antény rovnoběžné nejsou. Pak je třeba při řešení respektovat odlišnou prostorovou orientaci vektorů intenzity pole E_jk vůči povrchu j-tého vodiče. Po rozkladu vektorů E_jk na složky a využitím obecnějšího vyjádření příspěvku výkonu dP_Σ lze získat opět formálně výrazně složitější vztahy. Tak je možno řešit vazbu mezi zkříženými vodiči turniketové antény a další situace.