4.3 Yaggiho anténa

Základní teorie

V tomto odstavci budou poznatky získané v čl. 4.1 aplikovány a rozšířeny na případ Yagiho antény. Nejprve si uvedeme stručný popis této antény, dále pak princip její činnosti, a nakonec použijeme výsledky čl. 4.1 k vytvoření jejího numerického modelu.

Yagiho anténa [1] je řadovou soustavou dipólů s podélným vyzařováním, jejíž jeden prvek je galvanicky napájen (aktivní prvek) a ostatní prvky jsou napájeny vyzařovaným vlněním (pasivní prvky). V pasivních prvcích indukuje vlnění, které je vyzařováno prvkem aktivním, nezanedbatelné proudy, jež zpětně ovlivňují celou vyzařovací charakteristiku antény.

Díky konstrukční jednoduchosti a dobrým parametrům se Yagiho anténa stala jednou z nejrozšířenějších antén v pásmu metrových a decimetrových vln.

Jak již bylo řečeno, Yagiho anténa se skládá z jednoho aktivního prvku a několika prvků pasivních. Aktivním prvkem je symetrický dipól (nebo dipól skládaný), který většinou pracuje ve čtvrtvlnné rezonanci. Pasivní prvky jsou tvořeny dipóly bez napájecí štěrbiny. Jeden pasivní prvek, jehož délka je větší než délka aktivního prvku a jenž je umístěn vzadu, hraje roli reflektoru. Ostatní pasivní prvky, které jsou kratší než aktivní prvek a které jsou umístěny vpředu, jsou tzv. direktory (obr. 4.3A.1).

Dle počtu direktorů bývá zisk antény v rozmezí od 10 do 15 dB. Délky pasivních prvků vzhledem k délce aktivního prvku však nejsou zvoleny náhodně, nýbrž mají svoje opodstatnění v principu činnosti antény, což bude podrobněji vysvětleno níže.

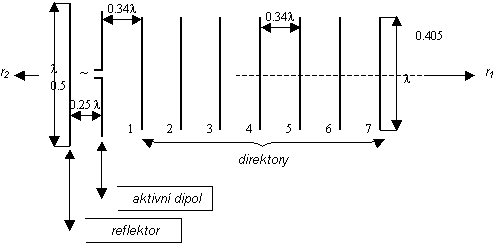
Obr. 4.3A.1

Yagiho anténa - popis a příklad realizace

Na obr. 4.3A.1 je uvedeno schéma Yagiho antény, která se skládá ze symetrického dipólu jako aktivního prvku, z reflektoru a ze sedmi direktorů. Při správném vyladění antény [6] reflektor zeslabuje tok energie ve směru r₂, a naopak první direktor zesiluje tok energie ve směru r₁. V tutéž dobu zesílení toku energie ve směru r₁ vytváří příznivé podmínky pro vybuzení druhého direktoru. Druhý direktor dodatečně zesiluje tok energie ve směru r₁ a vytváří tímto příznivé podmínky pro vybuzení třetího direktoru atd.

Z výše uvedeného plyne, že direktory tvoří svým způsobem vlnovodný kanál. Energie rozložená v tomto vlnovodném kanálu postupuje od aktivního prvku k nejvzdálenějšímu direktoru, a tam se částečně odráží. V konečném výsledku je celkové pole ve vlnovodném kanálu dáno superpozicí postupné a odražené vlny. Z tohoto úhlu pohledu je Yagiho anténa podobná anténám s postupnou vlnou.

Při náležitém seřízení direktorů je amplituda odražené vlny na posledním direktoru velmi malá a Yagiho anténa se chová podobně jako anténa s postupnou vlnou s přizpůsobenou zátěží na konci. Je však třeba říci, že Yagiho anténa se principiálně liší od obyčejných antén s postupnou vlnou tím, že rozložení proudu v ní v obecném případě nemusí být dáno superpozicí jedné postupné a jedné odražené vlny. V obecném případě je totiž rozložení proudu v Yagiho anténě popsáno součtem několika postupných a několika odražených vln, přičemž jednotlivé postupné a jednotlivé odražené vlny mají rozdílné konstanty šíření..

Má-li být vyzařovaná vlna ve směru r₂ zeslabována, musí být reflektor Yagiho antény navržen tak [6], aby se v něm indukovaný proud fázově předbíhal vzhledem k proudu v aktivním dipólu. Navíc intenzity polí od aktivního dipólu a od reflektoru musí mít takový příznivý poměr fází ve směru r₁, aby proud indukovaný v prvním direktoru byl fázově opožděn za proudem v aktivním dipólu (aby tok energie ve směru r₁ byl zesilován). Po dobně je nezbytné, aby byl proud indukovaný ve druhém direktoru fázově opožděn za proudem v prvním direktoru, proud ve třetím direktoru fázově opožděn za proudem ve druhém direktoru atd. Anténu je tedy nutno vyladit (seřídit) tak, aby výše uvedené podmínky byly splněny.

Elementární analýza, založená na metodě indukovaných elektromotorických napětí, ukazuje [6], že k dosažení výše popsaných fázových poměrů je třeba, aby celková impedance záření reflektoru (vztažená ke kmitně proudu) měla kladnou, induktivní reaktanci a aby celková impedance záření každého direktoru (opět vztažená ke kmitně proudu) měla zápornou, kapacitní reaktanci.

Znaménko reaktance prvků Yagiho antény můžeme ovlivnit změnou jejich délky. Kladné reaktance dosáhneme zvětšením délky prvku oproti jeho rezonanční délce, zápornou reaktanci získáme zkrácením délky prvku oproti jeho rezonanční délce [1]. Mluvíme-li o rezonanční délce, máme na mysli rezonanci čtvrtvlnnou.

Jelikož impedance záření dipólu závisí na jeho poloměru, je i velikost prodloužení či zkrácení jednotlivých prvků antény na tomto poloměru závislá. Kromě toho jsou výsledné hodnoty reaktancí reflektoru a direktorů závislé také na vzdálenostech mezi prvky antény a na počtu direktorů [6].

Na obr. 4.3A.1 uvádíme konkrétní parametry Yagiho antény [6] pro případ buzení symetrickým dipólem. Délka reflektoru je 0,5λ, délka direktorů je 0,405λ, délka aktivního odpovídá rezonanční délce (je o trochu kratší než 0,5λ). Čím menší je impedance záření aktivního dipólu, tím kratší je jeho rezonanční délka ve srovnání s 0,5λ. Průměr všech dipólů je 0,002λ. Rozteč mezi aktivním prvkem a reflektorem je 0,25λ, mezi aktivním prvkem a prvním direktorem je 0,34λ a mezi direktory navzájem je 0,34λ.

Yagiho anténa je v dnešní době velmi rozšířena. Existuje spousta realizací, které se vzájemně odlišují počtem direktorů, roztečemi mezi prvky a délkami prvků. Většinou bývají počty prvků, rozteče a délky stanovovány experimentálně. Rozvoj výpočetní techniky a numerických metod však dnes nabízí možnost modelovat a optimalizovat Yagiho anténu na PC. Této látce se budeme věnovat v dalších odstavcích. Abychom však mohli popisovanou látku plně pochopit, musíme znát teorii, uvedenou v čl. 4.1..

Dříve než přistoupíme k numerické analýze Yagiho antény, učiňme několik zjednodušujících předpokladů [7]:

Anténa je umístěna v bezeztrátovém prostředí.
Prvky antény jsou vyrobeny z dokonale vodivého materiálu.
Proud a náboje jsou vždy soustředěny v osách anténních vodičů.
Každý prvek antény (reflektor, dipól, direktory) je rozdělen na segmenty stejné délky.
Rozložení proudu na prvcích budeme aproximovat po částech konstantní funkcí (vícebázová aproximace).

Z bodu 2 plyne, že tečná složka intenzity elektrického pole musí být na každém segmentu antény nulová (vyjma napájecí štěrbiny dipólu). Dále je jasné, že pole na povrchu každého segmentu je ovlivněno nejenom proudy a náboji na tomtéž segmentu a na sousedních segmentech téhož anténního prvku, ale i proudy a náboji na segmentech ostatních prvků antény. To je hlavní rozdíl oproti případu, kdy jsme analyzovali pouze samotný dipól (čl. 4.1).

Nicméně základní kroky, vedoucí k sestavení impedanční matice Yagiho antény, jsou analogické ke krokům z čl. 4.1 o drátových anténách. Proto se omezíme pouze na úvahy týkající se modifikace výpočtu.

Pro výpočet impedanční matice osamoceného anténního prvku můžeme přímo použít vztahy (impedanční matici), které byly popsány v čl. 4.1.. V případě matice vzájemných impedancí dvou různých anténních prvků postupujeme v principu podobně jako v případě samotného prvku, ovšem s tím rozdílem, že do vzdálenosti zdrojového segmentu a segmentu cílového musíme včlenit vzájemnou prostorovou vzdálenost anténních prvků.

S využitím matic vzájemných impedancí a na základě druhého Kirchhoffova zákona můžeme pro Yagiho anténu psát následující lineární soustavu maticových rovnic:

pro reflektor:	$[0] = [Z_{r r}] [I_{r}] + [Z_{r d}] [I_{d}] + [Z_{r 1}] [I_{1}] + [Z_{r 2}] [I_{2}] + \dots + [Z_{r n}] [I_{n}]$ ,
pro aktivní dipól:	$[U_{0}] = [Z_{d r}] [I_{r}] + [Z_{d d}] [I_{d}] + [Z_{d 1}] [I_{1}] + [Z_{d 2}] [I_{2}] + \dots + [Z_{d n}] [I_{n}]$ ,
pro první direktor:	$[0] = [Z_{1 r}] [I_{r}] + [Z_{1 d}] [I_{d}] + [Z_{11}] [I_{1}] + [Z_{12}] [I_{2}] + \dots + [Z_{1 n}] [I_{n}]$ ,
pro n-tý direktor:	$[0] = [Z_{n r}] [I_{r}] + [Z_{n d}] [I_{d}] + [Z_{n 1}] [I_{1}] + [Z_{n 2}] [I_{2}] + \dots + [Z_{n n}] [I_{n}]$ ,

( 4.3A.1 )

kde [I_r] a [I_d] jsou vektory proudů v reflektoru a aktivním dipólu, [I₁], [I₂], ..., [I_n] jsou vektory proudů v prvním, ve druhém až v n-tém direktoru, [Z_rr], [Z_dd], [Z₁₁], [Z₂₂], ... , [Z_nn] jsou impedanční matice vzájemných impedancí segmentů na daném prvku (reflektoru, aktivním prvku, prvním direktoru, druhém direktoru až n-tém direktoru), [Z_rd] je impedanční matice vzájemných impedancí segmentů reflektoru a aktivního prvku, [Z_d1], ..., [Z_dn] jsou impedanční matice vzájemných impedancí segmentů aktivního prvku a prvního až n-tého direktoru, [Z_r1], ..., [Z_rn] jsou impedanční matice vzájemných impedancí segmentů reflektoru a prvního až n-tého direktoru, [Z_ik] je impedanční matice vzájemných impedancí i-tého a k-tého direktoru, [0] je nulový vektor, vektor [U₀] má všechny prvky nulové vyjma prvku, který odpovídá segmentu v místě napájení aktivního dipólu.

V důsledku reciprocity platí ještě následující vztahy:

[Z_{r d}] = {[Z_{d r}]}^{T}, [Z_{d n}] = {[Z_{n d}]}^{T}, [Z_{r n}] = {[Z_{n r}]}^{T}, [Z_{i k}] = {[Z_{k i}]}^{T}, [Z_{r r}] = {[Z_{r r}]}^{T}, [Z_{d d}] = {[Z_{d d}]}^{T}, [Z_{11}] = {[Z_{11}]}^{T}, \dots, [Z_{n n}] = {[Z_{n n}]}^{T}

kde písmenem ^T označujeme matici transponovanou.

Rozměr vektorů proudového rozložení na jednotlivých anténních prvcích [I_r], [I_d], [I₁], ..., [I_n] je roven počtu segmentů, na které je příslušný anténní prvek rozdělen. Matice vlastních impedancí jednotlivých anténních prvků [Z_rr], [Z_dd], [Z₁₁], ..., [Z_nn] jsou vždy čtvercové a jejich rozměr opět odpovídá počtu segmentů, na který je příslušný prvek rozdělen. Matice [Z_rd], [Z_dn], [Z_rn] a [Z_ik] mohou být v obecném případě obdélníkové (jednotlivé prvky antény se liší v počtu segmentů, na které jsou rozděleny) a mají rozměr R × D, D × N a R × N, kde R je počet segmentů reflektoru, D je počet segmentů aktivního dipólu a N je počet segmentů n-tého direktoru.

Soustavu rovnic (4.3A.1) je možno přepsat do kompaktnějšího tvaru

[Z] [I] = [U]

( 4.3A.2 )

kde

[Z] = [\begin{matrix} [Z_{r r}] & [Z_{r d}] & [Z_{r 1}] & \dots & [Z_{r n}] \\ [Z_{d r}] \\ [Z_{1 r}] \\ [Z_{n r}] & [Z_{n d}] & [Z_{n 1}] & [Z_{n n}] \end{matrix}], [I] = [\begin{matrix} [I_{r}] \\ [I_{d}] \\ [I_{1}] \\ [I_{n}] \end{matrix}], [U] = [\begin{matrix} [0] \\ [U_{0}] \\ [0] \\ [0] \end{matrix}]

( 4.3A.3 )

Matice [Z] je maticí symetrickou, tj. [Z] = [Z]^T.

Z rovnice (4.3A.2) můžeme vypočítat proudové rozložení na každém prvku antény.

Obr. 4.3A.2

Principiální schéma pro výpočet fázových rozdílů jednotlivých segmentů

[I] = {[Z]}^{- 1} [U]

( 4.3A.4 )

kde [Z]^-1 značí inverzní matici k matici [Z].

Vstupní impedanci antény pak můžeme vypočítat jako

Z_{v s t} = \frac{1}{{[Z]}_{f e e d, f e e d}^{- 1}} = \frac{1}{{[Y]}_{f e e d, f e e d}}

( 4.3A.5 )

kde feed je index prvku inverzní (admitanční) matice, který odpovídá tomu segmentu aktivního prvku, na nějž je přivedeno napájecí napětí U₀.

Pokud již známe proudové rozložení na jednotlivých prvcích antény, můžeme přikročit k výpočtu její směrové charakteristiky. Při výpočtu se zaměříme pouze na rovinu E (rovina, v níž leží anténa na obr. 4.3A.1; rovina H je kolmá k obrázku a k anténním prvkům). Jelikož každý segment, na něž jsou jednotlivé prvky antény rozděleny, můžeme pokládat za elementární dipól, lze pro intenzitu pole v okolí antény jakožto soustavy elementárních dipólů psát

E_{ϑ} = 60 j \frac{k}{2} \sin Θ \frac{\exp (- j k r)}{r} \sum_{n = 1}^{M} I_{n} \exp (- j k r Δ r_{n})

( 4.3A.6 )

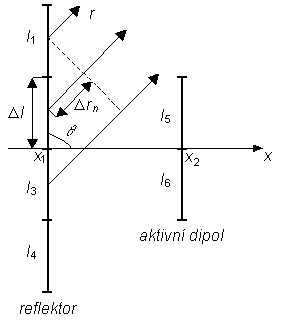
kde θ je úhel braný od osy dipólu, M je celkový počet segmentů celé antény, j je imaginární jednotka, k je vlnové číslo a Δr_n značí dráhové rozdíly vyzařovaných vln od jednotlivých elementárních dipólů (segmentů). Vše je ostatně názorně zobrazeno výše na obr. 4.3A.2.

Pro směrovou charakteristiku antény můžeme na základě (4.3A.6) psát

F (Θ) = j \frac{k}{2} \sin Θ \sum_{n = 1}^{M} I_{n} \exp (- j k Δ r_{n})

( 4.3A.7 )

Nyní již zbývá vypočítat dráhové rozdíly Δr_n vln vyzařovaných jednotlivými segmenty. Jako referenční segment vezmeme první segment reflektoru (viz obr. 4.3A.2). Potom můžeme pro dráhové rozdíly psát

pro první segment:	$Δ r_{1} = 0$
pro druhý segment:	$Δ r_{2} = Δ l \cos Θ$
pro třetí segment:	$Δ r_{3} = 2 Δ l \cos Θ$
pro čtvrtý segment:	$Δ r_{4} = 3 Δ l \cos Θ$
pro pátý segment:	$Δ r_{5} = (x_{1} - x_{2}) \sin Θ + Δ l \cos Θ$
pro šestý segment:	$Δ r_{6} = (x_{1} - x_{2}) \sin Θ + 2 Δ l \cos Θ$
atd.

( 4.3A.8 )

Obr. 4.3A.3

Rozložení proudu na dipólu

Na základě uvedeného popisu byl vytvořen matlabovský program, který je schopen analyzovat Yagiho anténu (bližší informace uvádíme ve vrstvě C a vrstvě D). Funkčnost programu si ověříme na tříprvkové soustavě (reflektor, aktivní dipól a direktor). Uvažujeme následující parametry:

Vlnová délka: 0.680 m
Délka reflektoru: 0.408 m
Poloměr vodičů: 0.001 m
Vzdálenost reflektor – dipól: 0.100 m
Vzdálenost dipól – direktor: 0.150 m
Délka dipólu: 0.357 m
Délka direktoru: 0.306 m
Reflektor: 15 stejných segmentů
Dipól 13 stejných segmentů
Direktor 11 stejných segmentů

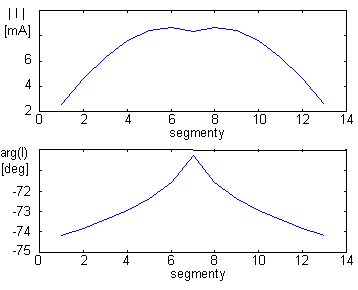
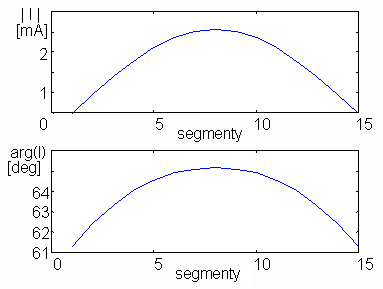
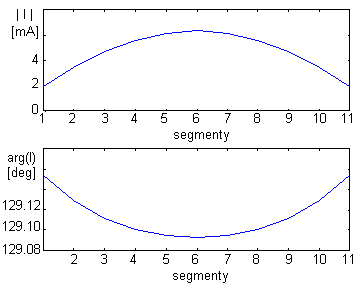
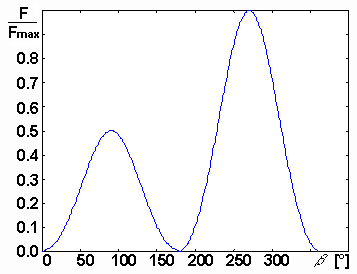
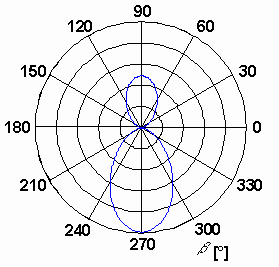
Na obr. 4.3A.3 až 4.3A.5 jsou vykresleny průběhy rozložení proudu na reflektoru, na dipólu a na direktoru. Na obr. 4.3A.6 a 4.3A.7 je znázorněna směrová charakteristika antény v kartézských a v polárních souřadnicích. Charakteristiky jsou zobrazeny v závislosti na úhlu β. Vztah mezi úhlem β a θ z obrázku 4.3A.2 je θ = 360° - β.

Obr. 4.3A.4

Rozložení proudu na reflektoru

Obr. 4.3A.5

Rozložení proudu na direktoru

Obr. 4.3A.6

Kartézská charakteristika

Obr. 4.3A.7

Polární charakteristika

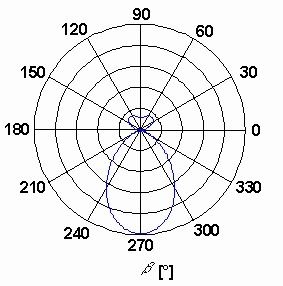
Obr. 4.3A.8

Polární charakteristika

Na obrázcích směrových charakteristik (obr. 4.3A.6 a 4.3A.7) si můžeme všimnout, že záření antény ve směru od dipólu k direktorům (β = 270°) je znatelně silnější než ve směru opačném. Ještě dominantnějšího hlavního laloku můžeme dosáhnout tím, že sledovanou anténní soustavu rozšíříme o dva direktory. Všechny parametry budou stejné jako v předchozím případě s tímto rozdílem:

První direktor je vzdálen 0.107 m od dipólu.
Druhý direktor je vzdálen 0.150 m od dipólu.
Třetí direktor je vzdálen 0.272 m od dipólu.

Na obrázku 4.3A.8 tedy máme výslednou směrovou charakteristiku antény v polárních souřadnicích.

Závěrem je třeba říci, že existuje více možností, jak analyzovat Yagiho anténu (např. a priori předpokládáme sinusovou proudovou distribuci na každém prvku antény, a dále jen určíme např. vstupní impedanci a směrovou charakteristiku antény [6]). Je ovšem jasné, že výsledky dosažené tímto postupem jsou méně přesné, než výsledky vypočtené momentovou metodou. V dnešní době, kdy máme k dispozici dostatečně výkonné počítače, je vhodnější pro návrh použít numerického modelování.