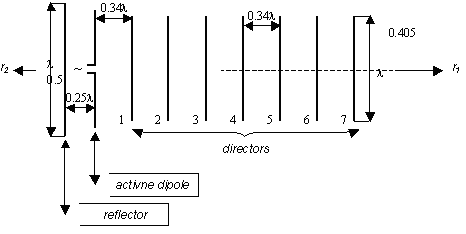
4.3 Yagi antennaBasic theoryIn this paragraph, the knowledge from the paragraph 4.1 is going to be applied and extended to modeling Yagi antenna. First, a brief description of the antenna is given. Second, the principle of its operation is explained, and third; results of the paragraph 4.1 are exploited in order to build a numerical model of the antenna. Yagi antenna [1] is a row of dipoles exhibiting longitudinal radiation. A single element (active one) is fed in galvanic way and the rest of elements are excited by the radiation (passive elements). In passive elements, the wave, which is radiated by the active element, induces currents those regressively influence the radiation pattern of the whole antenna. Thanks to the construction simplicity and good parameters, Yagi became one of the most popular antennas in the meter-wave band and decimeter-wave one. As already noted, Yagi antenna consists of a single active element and several passive ones. As an active element, a symmetric dipole (or a folded one), which works in one-quarter-wavelength resonance, is used. Passive elements are constructed as dipoles without the excitation gap. A single passive element, which is longer than the active one, is positioned at the back and plays the role of a reflector. The rest of passive elements, which are shorter than the active one, are placed in the front and are called directors (fig. 4.3A.1). Depending on the number of directors, the gain of the antenna is between 10 and 15 dB. Lengths of passive elements with respect to the length of the active one are not chosen randomly but their proper value conditions a proper functionality of the antenna.
In fig. 4.3A.1, the schematic of Yagi antenna is given. The antenna consists of a symmetric dipole as an active element, of a reflector and of seven directors. If the antenna is properly tuned [6], the reflector attenuates the energy flow in the direction r2, and the first director amplifies the energy flow in the direction r1. At the same moment, amplification of the energy flow in the direction r1 creates conditions for the excitation of the second director. The second director subsequently amplifies the energy flow in the direction r1 and creates conditions for the excitation of the third director, etc. We can therefore say that directors form a wave-guiding channel in a fact. Energy distributed in this wave-guiding channel travels from the active element to the director in the largest distance, and there, the wave is partially reflected. As a result, the total field in the wave-guiding channel is given by the superposition of the forward wave and the backward one. From that point of view, Yagi antenna belongs to the traveling wave antennas. If directors are properly tuned, amplitude of the reflected wave at the last director is very small, and Yagi antenna behaves as a traveling wave antenna, which is matched at its end. Nevertheless, Yagi antenna differs from traveling wave antennas in principle because the current distribution need not be the superposition of a single forward wave and a single backward one. In general, the current distribution of Yagi antenna can be described by the sum of several forward waves and backward ones, which are of different propagation constants. If the radiated wave should be attenuated in the direction r2, the reflector of Yagi antenna has to be designed that way [6] so that the phase of induced current anticipates the current phase in the active dipole. Moreover, field intensities of the active dipole and of the reflector have to be of such phases in r1, so that the phase of the current induced in the first director can be retarded with respect to the active dipole (so that the energy flow in r1 can be amplified). Similarly, phase of the current induced in the second director has to be retarded with respect to the first director, etc. The antenna has to be tuned so that all the above-described conditions are fulfilled. An elementary analysis, which is based on the method of induced electromotoric forces, shows [6], that the total radiation impedance of the reflector (related to the maximal current) has to be of positive, inductive reactance and that the total radiation impedance of each director (related to the maximal current) has to be of negative, capacitive reactance. The polarity of the reactance of elements of Yagi antenna can be influenced changing their length. Positive reactance is reached by increasing the length with respect to resonant one, and vice versa [1]. Speaking about the resonant length, one-quarter-wavelength resonance is assumed. Since radiation impedance of the dipole depends on its radius, even the magnitude of shortening or extending antenna elements depends on this radius. Moreover, resultant values of reactance of the reflector and the directors depend on the distances among antenna elements and on the number of directors [6]. In fig. 4.3A.1, concrete parameters of Yagi antenna are given [6] when symetric dipole is used as an active element. The length of the reflector is 0.5λ, the length of the directors is 0.405λ, the length of the active element corresponds to the resonant length; is a bit shorter than 0.5λ. Smaller the radiation impedance of the active dipole is, shorter its resonant length (with respect to 0.5λ) is. Diameter of all the dipoles equals to 0.002λ. The distance between the active element and the reflector equals to 0.25λ, the distance between the active element and the first director is 0.34λ, and the distance among directors equals to 0.34λ. Yagi antenna is very popular these days. There are many technical realizations of this antenna, which differ in the number of directors, distances among antenna elements and lengths of those elements. In most cases, the number of elements, distances and lengths are determined experimentally. Nevertheless, today's computers and advanced numerical techniques enable to develop efficient computer programs for modeling and optimizing Yagi antennas on a PC. This topic is going to be investigated in the next paragraphs. In order to fully understand the explanation, the theory presented in the paragraph 4.1 has to be studied. Before starting the numerical analysis of Yagi antenna, several simplifications are introduced [7]:
As a consequence of the assumption 2, the tangential component of electric field intensity has to be zero on each antenna segment except of the excitation gap. Obviously, field on the surface of each antenna segment is influenced not only by currents and charges of the respective antenna element but too by currents and charges of other antenna elements. This it the main difference compared to a simple dipole analysis in the paragraph 4.1. Nevertheless, the main steps of building the impedance matrix of Yagi antenna are done in analogy with the wire antenna approach. Therefore, modifications of the computational algorithm are described here only. Computing impedance matrix of the stand-alone active antenna element, relations described in paragraph 4.1 can be directly applied. In case of two different antenna elements, the mutual impedance of segments is computed a similar way; moreover the mutual distance of antenna elements has to be included to the computation of the distance between two respective segments. Using matrices of mutual impedances and second Kirchhoff low, the following set of linear matrix equations is obtained for Yagi antenna:
here, [Ir] and [Id] are vectors of currents in the reflector and in the active dipole, [I1], [I2], ..., [In] are vectors of currents in the first director, in the second one, up to the n-th one. Next, [Zrr], [Zdd], [Z11], [Z22], ... , [Znn] are impedance matrices containing mutual impedances of segments belonging to a given element (reflector, active element, first director, second director up to the n-th director), [Zrd] denotes the matrix of mutual impedances between segments of the reflector and the active dipole, [Zd1], ..., [Zdn] are matrices of mutual impedances between segments of the active dipole and directors, [Zr1], ..., [Zrn] denote matrices of mutual impedances between segments of the reflector and directors, [Zik] is matrix of mutual impedances between segments of i-th and k-th director, [0] is zero vector, the vector [U0] contains a single non-zero element corresponding to the voltage in the excitation gap of the active dipole. Considering the principle of the reciprocity, following relations can be obtained:
Here, T denotes the matrix transposition. The size of vectors of current distribution on respective antenna elements [Ir], [Id], [I1], ..., [In] equals to the number of segments, the element is divided for. The matrix of self-impedances of antenna elements [Zrr], [Zdd], [Z11], ..., [Znn] are square matrices, which size corresponds to the number of segments again. Matrices [Zrd], [Zdn], [Zrn] and [Zik] can be in general rectangular and are of the size R x D, D x N and R x N, where R is the number of segments of the reflector, D is the number of segments of the active dipole and N is the number of segments of the n-th director. The set of equations (4.3A.1) can be rewritten to a more compact form:
where
The matrix [Z] is symmetric, i.e. [Z] = [Z]T. Solving eqn. (4.3A.2), current distribution on every antenna element can be computed
where [Z]-1 denotes the inverse of the matrix [Z]. Input impedance of the antenna is computed as
where feed is the index of the element of the inverted (admitance) matrix, which corresponds to the excitation segment of the active element. If the current distribution on antenna elements is known, directivity pattern can be computed. In our computations, only the plane E is considered (the plane identical with fig. 4.3A.1; the plane H is perpendicular to the Figure and to antenna elements as well). Since each discretization segment of the antenna can be considered as an elementary dipole, the following relation can describe electric field intensity in the surrounding of the antenna:
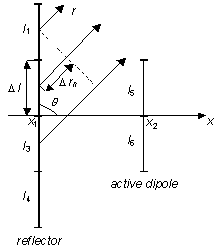
Here, θ is an angle measured from the dipole axis, M is the total number of segments of the whole antenna, j denotes imaginary unit, k is wave-number, and Δrn denotes spatial differences of waves radiated by different elementary dipoles (segments). The rest of symbols is explained in fig. 4.3A.2. The directivity pattern of the antenna can be expressed considering (4.3A.6) as
Finally, spatial differences of waves Δrn have to be expressed for all the segments of the antenna. As a reference, the first segment of the reflector is elected (see fig. 4.3A.2). Then, spatial difference are described by the following equations:
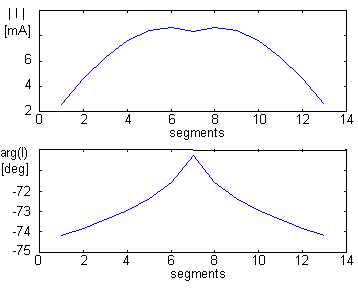
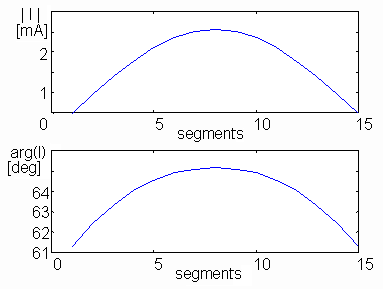
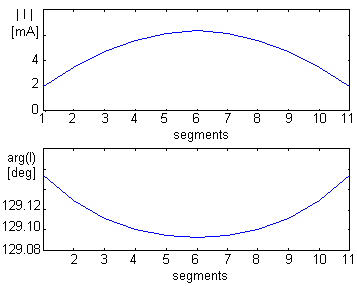
On the basis of the above-given description, a Matlab program for the analysis of Yagi antenna was developed (for more information, see the layer C and the layer D). Functionality of the program is verified by analyzing a three-element Yagi antenna (reflector, active dipole and director). Following parameters are considered:
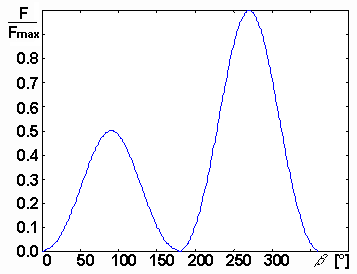
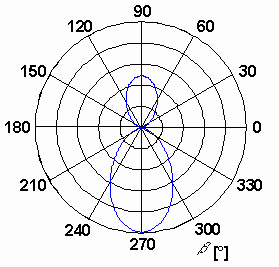
Fig. 4.3A.3 to 4.3A.5 show the current distribution on the reflector, on the dipole and on the director. Fig. 4.3A.6 to 4.3A.7 show the directivity pattern of the antenna both in the Cartesian coordinates and in the polar ones. In patterns, the angle β is related to the angle θ as depicted in fig. 4.3A.2: θ = 360° - β.
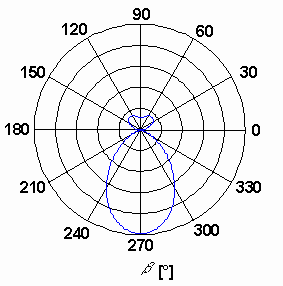
Directivity patterns (fig. 4.3A.6 and 4.3A.7) show that the antenna radiation is much stronger in the direction from the dipole to the directors (β = 270°) than in the opposite direction. Extending the antenna for additional two directors can create even more dominant main beam. The rest of the parameters stay the same except of:
Fig. 4.3A.8 shows the final directivity pattern of the antenna in polar coordinates. We can conclude that there are more ways of analyzing Yagi antenna (e.g., sine current distribution is a priori assumed on each antenna element, and consequently, input impedance and directivity pattern are computed [6]). Obviously, the moment method is able to reach better accuracy. These days, when powerful computers are at our disposal, the moment method is highly preferred. |