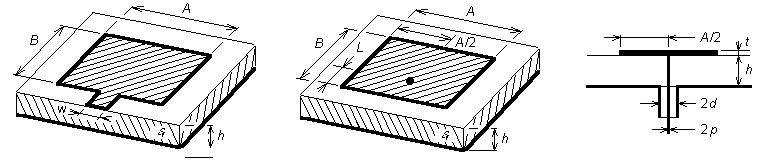
4.4 Mikropáskový dipól

Základní teorie

Mikropáskové antény jsou v současných systémech bezdrátových komunikací velice rozšířeným druhem antén. Je to dáno tím, že tyto antény vynikají velice nízkým profilem, a proto mohou být bez větších potíží umísťovány na trupy letadel, na stěny budov, či na odvrácené strany mobilních telefonů. Navíc, mikropáskové antény jsou vyráběny stejnou technologií jako tištěné spoje, a proto je jejich výroba velmi levná a dobře reprodukovatelná. Konečně, mikropáskové antény lze velice snadno integrovat přímo do mikrovlnných obvodů, založených na mikropáskové technologii, a tudíž není zapotřebí žádných speciálních vedení, symetrizačních členů či konektorů, jako je tomu v případě většiny antén klasických [8].

Nicméně, mikropáskové antény mají i své stinné stránky. Hlavní nevýhodou těchto antén přitom bývá jejich úzkopásmovost. Díky této úzkopásmovosti je pak velmi složité navrhovat mikropáskové anténní řady s dostatečně nízkou úrovní bočních laloků. Problémy mohou vznikat i s napájecím mikropáskovým vedením: jeho parazitní vyzařování může deformovat směrovou charakteristiku [8].

Jeden z nejčastěji používaných typů mikropáskové antény je schématicky nakreslen na obr. 4.4A.1a (patch antenna, v české literatuře se někdy používá termín flíčková anténa). Anténu tvoří vodivý obdélník o rozměrech A × B, který je nanesený na dielektrickém substrátu. Anténa bývá napájena mikropáskovým vedením (na obr. 4.4A.1 vede mikropásek z dolní hrany substrátu šikmo zleva). Druhá strana substrátu (na obr. 4.4A.1a je nakreslena jako spodní) je souvisle pokovena. Tato pokovená strana tvoří jakýsi reflektor alespoň v tom smyslu, že má (z hlediska napájení) nulový potenciál a že omezuje vyzařování směrem dolů. V dalším textu tuto plochu nazýváme zemní plochou.

Na mikropáskovou anténu, napájenou mikropáskovým vedením (obr. 4.4A.1a) můžeme pohlížet jako na otevřené (nestíněné) mikropáskové vedení na konci naprázdno, které je u konce výrazně rozšířeno. Pokud se podél tohoto mikropáskového vedení šíří elektromagnetická vlna, dochází na nehomogenitách (skokové rozšíření mikropásku na hranici mezi napájecím vedením a anténním prvkem a otevřený konec vedení na konci mikropáskového elementu) k vyzařování elektromagnetické energie do okolního prostoru. Struktura se tedy chová jako vysílací anténa. Pokud je navíc délka mikropáskového anténního prvku rovna polovině vlnové délky na tomto rozšířeném vedení, vstupní impedance antény je čistě reálná [8]. Říkáme, že anténa je v rezonanci.

Vyzařování mikropáskové antény je možno vysvětlit i jinými způsoby. Můžeme např. vycházet z rozložení proudu na mikropáskovém anténním prvku, na který se pak můžeme dívat jako na drátovou anténu, sestávající z velmi širokého a velmi tenkého anténního vodiče. Nebo můžeme vyjít ze siločar vektoru elektrické intenzity na přední a na zadní hraně anténního prvku (z hlediska napájecího mikropásku) a vyzařování můžeme vysvětlit pomocí výrazné horizontální složky (tj. složky rovnoběžné se zemní plochou) vektoru elektrické intenzity na těchto hranách.

Alternativou k napájení mikropáskové antény mikropáskovým vedením je napájení koaxiálním kabelem (obr. 4.4A.1b). Zatímco vnější vodič koaxiálního kabelu je připojen k zemní desce, vnitřní vodič prochází otvorem v této zemní ploše směrem do dielektrického substrátu a přes něj pokračuje k mikropáskovému anténnímu prvku, na který je napojen (obr. 4.4A.1c). Velkou výhodou koaxiálního napájení je přitom výrazné potlačení parazitního vyzařování napájecího vedení [8].

Obr. 4.4A.1

Mikropásková anténa, sestávající z jediného obdélníkového mikropáskového anténního prvku.
a) napájení mikropáskovým vedením
b) napájení koaxiálním vedením
c) průřez anténou b) v rovině středního vodiče koaxiálního napaječe

Na druhou stranu však při koaxiálním napájení ztrácíme jednu významnou přednost mikropáskových antén, a to snadnou realizaci napájecího systému při sdružování mikropáskových anténních prvků do anténních soustav.

Nyní se však již věnujme matematickému modelování mikropáskových antén.

Díky velkému zájmu o tyto antény vzniklo a stále vzniká velké množství jejich různých modelů, které se od sebe v různých aspektech odlišují. Numerické modely mají různé obory platnosti (některé modely jsou dostatečně přesné pouze pro nižší mikrovlnné kmitočty, jiné platí jen v omezeném intervalu rozměrů). Velké rozdíly mezi numerickými modely jsou rovněž v jejich výpočetní náročnosti (zatímco některé modely je možno popsat vztahy v uzavřeném tvaru, takže jejich výpočetní nároky jsou minimální, jiné modely jsou založeny na numerických metodách, takže při dostatečně jemné diskretizaci musíme pracovat s rozlehlými maticemi, a tudíž potřebujeme velký výpočetní výkon). Velké odlišnosti jsou mezi metodami i v dosahované přesnosti.

My se budeme v našem výkladu věnovat modelování mikropáskových antén pomocí momentové metody, se kterou jsme se již seznámili v čl. 4.1. Jak již bylo řečeno, tato metoda vychází z Maxwellových rovnic v integrálním tvaru, takže namísto hledání rozložení elektrických a magnetických intenzit v celém okolí antény nám stačí pracovat s napětími a proudy na mikropáskovém anténním prvku.

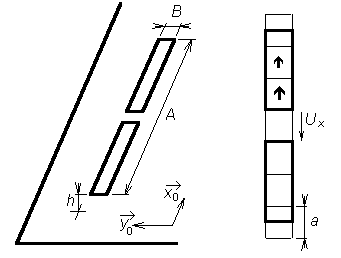
Obr. 4.4A.2

Mikropáskový dipól s reflektorem.
a) celkový pohled
b) diskretizační síť pro x-ovou složku proudové hustoty

V tomto článku učebnice si přitom situaci zjednodušíme. Nebudeme se totiž zabývat analýzou flíčkové antény, ale pouze analýzou symetrického mikropáskového dipólu, který je nakreslen na obr. 4.4A.2. U dipólu budeme předpokládat velmi malou šířku anténního mikropásku B. Potom po anténním vodiči potečou proudy pouze v podélném směru (směr x) a nám stačí řešit jednorozměrný problém, který je analogický k drátovému dipólu (čl. 4.1).

Při analýze budeme předpokládat nekonečně velkou plochu substrátu, nekonečně malou tloušťku pokovení t ≈ 0, dokonalou elektrickou vodivost všech kovových ploch, bezeztrátovost dielektrika a takové parametry volného prostoru okolo antény, které odpovídají parametrům vakua.

Předpokládejme, že na mikropáskový dipól dopadá rovinná vlna s úhlovým kmitočtem ω, která je popsána vektorem elektrické intenzity E^I (horní index I symbolizuje dopadající vlnu, anglicky incident). Tato vlna na anténním vodiči indukuje vodivé proudy, které jsou popsány vektorem proudové hustoty J. Jelikož na koncích mikropáskového dipólu nemají elektrické proudy kam téci, hromadí se zde náboj, popsaný nábojovou hustotou ρ. V následující půlvlně, kdy se mění orientace tečení vodivých proudů, náboj akumulovaný na ramenech dipólu odtéká [9].

Působení proudů můžeme popsat pomocí vektorového potenciálu

A (r) = \iint_{S} {G_{A} (r | r_{0}) \cdot J (r_{0})} d S_{0}

( 4.4A.1a )

působení nábojů pomocí potenciálu skalárního

V (r) = \iint_{S} {G_{V} (r | r_{0}) ρ (r_{0})} d S_{0}

( 4.4A.1b )

Hodnotu vektorového potenciálu A(r) v cílovém bodě r na mikropáskovém dipólu vypočteme postupným sčítáním příspěvků složek vektoru proudové hustoty J ze všech bodů mikropáskového anténního prvku r₀, přičemž tento vektor proudové hustoty J vždy násobíme příslušným sloupcem dyadické Greenovy funkce G_A. Na cílový bod, v němž hodnotu vektorového potenciálu počítáme, ukazuje polohový vektor r. Sčítání příspěvků všech proudů tekoucích po povrchu mikropáskového dipólu k vektorovému potenciálu A(r) v bodě r provádí integrál přes celou plochu mikropáskového dipólu S. Na všechny zdrojové body, v nichž se nacházejí proudy přispívající k vektorovému potenciálu v bodě r, postupně ukazuje během integrace polohový vektor r₀. Argumentem dyadické Greenovy funkce r|r₀ se tedy snažíme naznačit, že právě počítáme příspěvek proudu v bodě r₀ k potenciálu v bodě r.

Co se týká vztahu pro výpočet skalárního potenciálu, dyadická Greenova funkce G_A je nahrazena skalární Greenovou funkcí G_V a místo vektoru proudové hustoty vystupuje ve vztahu skalární hustota nábojová ρ. Vše ostatní ve vztahu (4.4A.1b) zůstává beze změny vůči (4.4A.1a).

Jak jsme zmínili výše, proudová a nábojová hustota na mikropáskovém dipólu jsou vzájemně svázány. Proto musíme vztahy (4.4A.1a) a (4.4A.1b) doplnit rovnicí kontinuity, která tuto vazbu matematicky popisuje

- j ω ρ = \nabla \cdot J

( 4.4A.1c )

Vztah (4.4A.1c) v podstatě říká, že proud vytékající z určité uzavřené oblasti (viz divergence proudu na pravé straně) musí být roven poklesu náboje v této oblasti za jednotku času (viz záporná časová derivace nábojové hustoty na straně levé).

Máme-li vyjádřen jak vektorový tak skalární potenciál na ploše mikropáskového dipólu, můžeme konečně vypočíst elektrickou intenzitu vlny, která je vyzařována naší anténou

E^{S} = - j ω A - \nabla V

( 4.4A.1d )

Časová derivace vektorového potenciálu jωA popisuje dynamický příspěvek elektrických nábojů na dipólu k vyzařované vlně (zdrojem vektorového potenciálu jsou totiž elektrické vodivé proudy, náboje v pohybu). Gradient skalárního potenciálu vyjadřuje statický příspěvek elektrických nábojů na mikropásku k vyzařované vlně (zdrojem skalárního potenciálu jsou v tuto chvíli statické náboje, koncentrované v blízkosti konců dipólu).

Konečně poslední záležitostí, o kterou se musíme postarat, jsou okrajové podmínky. Jelikož všechny kovové části naší antény jsou dokonale elektricky vodivé, musejí být složky vektoru elektrické intenzity, jež jsou k těmto plochám tečné, na těchto dokonalých plochách nulové

n_{0} \times E^{S} = - n_{0} \times E^{I}

( 4.4A.1e )

Ve výše uvedeném vztahu značí E^S vektor elektrické intenzity vlny, která je anténou vyzařována, a E^I je vektor elektrické intenzity vlny dopadající na anténu zvnějšku. Vektor n₀ je jednotkovým vektorem, kolmým k dokonale elektricky vodivým plochám.

Jak jsme se již zmínili v čl. 4.1, analytické řešení systému rovnic (4.4A.1) není známo, a proto jej budeme řešit pro náš mikropáskový dipól numericky pomocí momentové metody.

V prvém kroku analýzy elektromagnetického pole naší mikropáskové antény si umístíme tuto anténu do kartézského souřadného systému (obr. 4.4A.2). Dále, vektorové rovnice (4.4A.1) přepíšeme ve zvoleném souřadném systému do rovnic skalárních. Navíc budeme uvažovat ten speciální případ, kdy se pohybujeme na ploše mikropáskového dipólu (zde známe díky okrajovým podmínkám hodnotu tečné složky elektrické intenzity, což v dalším s výhodou využijeme).

Začněme vztahem (4.4A.1a), který nám popisuje závislost vektorového potenciálu na vektorech proudových hustot. Vzájemný vztah mezi těmito dvěma veličinami je popsán dyadickou Greenovou funkcí. Jedná se v podstatě o matici 3 × 3, jejímiž prvky jsou funkce popisující závislost složek x, y, z vektorového potenciálu na složkách vektoru proudové hustoty. Skalární složka G_A^st této dyadické Greenovy funkce může být tedy chápána jako s-tá složka vektorového potenciálu, jejímž zdrojem je elementární elektrický dipól (popsaný konstantním vektorem proudové hustoty), který je orientován do směru t. Je tedy zřejmé, že v našem případě bude mít dyadická Greenova funkce nenulovou pouze složku xx (za předpokladu velmi malé šířky mikropáskového dipólu je y-ová složka vektoru proudové hustoty nulová a jediná nenulová J_xx může být zdrojem jen x-ové složky vektorového potenciálu A_x; ostatní složky vektoru A budou nabývat nulové hodnoty).

Hodláme-li tedy vypočíst x-ovou složku vektorového potenciálu (tedy složku, která leží na ploše mikropáskového dipólu), přejde vztah (4.4A.1a) na tvar

A_{x} (x_{m}, y_{n}) = \iint_{S} {G_{A}^{x x} (x_{m}, y_{n} | x^{'}, y^{'}) J_{x} (x^{'}, y^{'})} d x^{'} d y^{'}

( 4.4A.2 )

Zde přitom značí (x_m, y_n) souřadnice bodu na ploše dipólu, v němž počítáme složku vektorového potenciálu A_x. Souřadnice (x', y') udávají polohu x-ové složky vektoru proudové hustoty, která přispívá k x-ové složce vektorového potenciálu. Souřadnice (x', y') se přitom během integrace postupně posunují po celé ploše dipólu S. Symbol J_x označuje x-ovou složku vektoru proudové hustoty, symbol G_a^xx reprezentuje x-ový diagonální člen dyadické Greenovy funkce.

Tím máme vztah (4.4A.1a) upraven pro speciální případ naší antény, a tudíž můžeme dále pokračovat úpravou rovnice (4.4A.1b). Protože se jedná o skalární vztah, obsahující pouze skalární veličiny, stačí nám v podstatě pouze pozměnit jeho formu tak, aby odpovídala zavedené souřadné soustavě

V (x_{m}, y_{n}) = \iint_{S} {G_{V} (x_{m}, y_{n} | x^{'}, y^{'}) ρ (x^{'}, y^{'})} d x^{'} d y^{'}

( 4.4A.3 )

Připomeňme, že skalární potenciál V opět počítáme na ploše dipólu, a to v bodě (x_m, y_n). Při výpočtu tohoto potenciálu integrujeme po celé ploše dipólu součin skalární Greenovy funkce G_V a nábojové hustoty ρ. Posuv po ploše dipólu během integrace je přitom realizován změnou souřadnic (x', y').

Dále se věnujme rovnici kontinuity (4.4A.1c). Jelikož vektor proudové hustoty má pouze x-ovou složku (vodivé proudy mohou téci jen ve směru dipólu), můžeme tento vztah přepsat do tvaru

- j ω ρ (x, y) = \frac{\partial J_{x} (x, y)}{\partial x}

( 4.4A.4 )

Z (4.4A.4) můžeme vyjádřit nábojovou hustotu ρ jako funkci proudové hustoty J_x a můžeme ji dosadit do (4.4A.3). Tím vyloučíme ze vztahu (4.4A.3) nábojovou hustotu a oba potenciály budou pouze funkcemi složek vektoru hustoty proudové

V (x_{m}, y_{n}) - \frac{1}{j ω} \iint_{S} {G_{V} (x_{m}, y_{n} | x^{'}, y^{'}) [\frac{\partial J_{x} (x^{'}, y^{'})}{\partial x}]} d x^{'} d y^{'}

( 4.4A.5 )

V předposledním kroku dosadíme vektorový potenciál (4.4A.2) a skalární potenciál (4.4A.5) do vztahu (4.4A.1d), který nám umožňuje z těchto potenciálů vypočítat elektrickou intenzitu vyzařované vlny. Protože jak potenciál vektorový (4.4A.2) tak skalární (4.4A.5) jsou funkcemi neznámého rozložení proudové hustoty na ploše dipólu, bude i elektrická intenzita funkcí tohoto rozložení

E_{x}^{S} (x_{m}, y_{n}) = - j ω A_{x} (x_{m}, y_{n}) - \frac{\partial V (x_{m}, y_{n})}{\partial x}

E_{x}^{S} (x_{m}, y_{n}) = - j ω \iint_{S} {G_{A}^{x x} (x_{m}, y_{n} | x^{'}, y^{'}) J_{x} (x^{'}, y^{'})} d x^{'} d y^{'} + \frac{1}{j ω} \iint_{S} \frac{\partial}{\partial x} {G_{V} (x_{m}, y_{n} | x^{'}, y^{'}) [\frac{\partial J_{x} (x^{'}, y^{'})}{\partial x}]} d x^{'} d y^{'}

( 4.4A.6 )

Velikost elektrické intenzity na ploše mikropáskového dipólu jsme schopni určit za předpokladu jeho dokonalé vodivosti z okrajové podmínky (4.4A.1e). Jedinou neznámou ve vztahu (4.4A.6) je tudíž proudová hustota J_x. A právě rovnici (4.4A.6) s neznámou funkcí J_x(x, y) budeme řešit momentovou metodou.

Postup, jakým z (4.4A.6) získáme po částech konstantní aproximaci proudového rozložení na dipólu, jsme popsali již ve čl. 4.1.. Proto si nyní tento postup jen stručně připomeňme.

Oblast, v které hledáme řešení integrální rovnice, musíme diskretizovat (plochu dipólu rozdělíme na vzájemně se nepřekrývající podoblasti, které spolu dohromady pokrývají celý analyzovaný dipól, viz obr. 4.4A.2b).
Při diskretizaci je nutno vzít v úvahu okrajové podmínky, které musejí být hledanými funkcemi splněny. V našem případě to znamená, že x-ová složka vektoru proudové hustoty J_x musí být nulová na hranách x = 0, x = A. Na konce dipólu se totiž můžeme dívat jako na otevřené konce mikropáskového vedení (na nich musejí ležet uzly proudu).
Při použití po částech konstantní aproximace složek vektoru proudové hustoty zajistíme splnění okrajových podmínek velmi jednoduše. Diskretizační síť přetáhneme o polovinu výšky diskretizačního prvku, a poté vnutíme těmto diskretizačním prvkům nulovou hodnotu proudu (viz obr. 4.4A.2b).
Hledanou funkci J_x(x, y) aproximujeme na základě bázových funkcí (nabývají jednotkové hodnoty nad plochou jedné buňky a nulové hodnoty nad plochami ostatních buněk), a na základě neznámých aproximačních koeficientů
${\tilde{J}}_{x}^{(n)} (x, y) = \sum_{n x = 1}^{N x} J_{x}^{(n x)} Π^{(n x)} (x, y)$ . ( 4.4A.7 )
Ve výše uvedeném vztahu značí J_x^~(n) aproximaci x-ové složky vektoru proudové hustoty nad plochou n-té buňky, J_x^(nx) je vzorek přesné hodnoty této složky uprostřed n-té buňky, Π^(nx) značí bázovou funkci, jejíž hodnota je jednotková v oblasti buňky číslo nx a nulová v oblastech ostatních buněk, a Nx je celkový počet buněk, z nichž sestává diskretizační síť pro výpočet proudové hustoty.
Aproximaci (4.4A.7) dosadíme do výchozí rovnice (4.4A.6). Jelikož však aproximace (4.4A.7) nesplňuje výchozí rovnici (4.4A.6) přesně, musíme tuto skutečnost respektovat přidáním zbytkové funkce R_x(x, y) do vztahů (4.4A.6) společně s aproximací (4.4A.7)
$R_{x} (x, y) = E^{S} (x, y) - \sum_{n x = 1}^{N x} {J_{x}^{(n x)} \iint_{S} [G_{A}^{x x} (x, y | x^{'}, y^{'}) + {\bar{G}}_{V} (x, y | x^{'}, y^{'})] d x^{'} d y^{'}}$ . ( 4.4A.8 )
V těchto vztazích značí G_A^xx x-ový diagonální člen dyadické Greenovy funkce a pomocí G^¯_V symbolizujeme parciální derivaci skalární Greenovy funkce v posledním členu ve vztahu (4.4A.6).
Protože bázové funkce Π jsou na ploše příslušného diskretizačního prvku vždy jednotkové a na plochách ostatních prvků nulové, ve výše uvedeném zápisu se neprojeví. Dále by mělo být z tvaru výše uvedených vztahů zřejmé, že jsme při jejich odvozování zaměnili pořadí integrace a sumace a že jsme aproximační koeficienty J_x^nx, které jsou na ploše diskretizačního prvku vždy konstantní, vytkli před příslušné integrály.
Zbytkovou funkci R_x(x, y) se budeme snažit minimalizovat. Čím nižších funkčních hodnot bude totiž zbytková funkce nabývat, tím více se bude naše aproximace přibližovat přesnému řešení. K minimalizaci přitom opět využijeme metodu vážených reziduí
$\iint_{S} {W_{x} (x, y) R_{x} (x, y)} d x d y = 0$ . ( 4.4A.9 )
Ve výše uvedených vztazích značí R_x zbytkovou funkci počítanou podle (4.4A.8). Symbol W_x pak představuje vhodně zvolené váhové funkce. Váhovat budeme opět Diracovými impulsy, abychom se díky jejich filtrační vlastnosti zbavili jednoho integrování
$\iint_{S} {δ (x - x_{m}, y - y_{n}) R_{x} (x, y)} d x d y = R_{x} (x_{m}, y_{n})$ . ( 4.4A.10 )
Přesnost metody, která využívá pro váhování Diracových impulsů, nemůže být příliš vysoká, protože díky těmto impulsům neminimalizujeme chybu aproximace globálně v celé analyzované oblasti, ale pouze v bodech, ve kterých Diracovy impulsy nabývají nenulové hodnoty (pracujeme jen s momenty zbytkové funkce).
Použijeme-li při váhování stejný počet váhových funkcí jako je počet neznámých aproximačních koeficientů, dospějeme k soustavě N lineárních rovnic pro N neznámých. Vyřešením této soustavy získáme dosud neznámé hodnoty aproximačních koeficientů, a tudíž budeme schopni sestavit aproximaci rozložení proudu na mikropáskovém dipólu. Ze známého proudového rozložení pak můžeme vypočíst všechny požadované technické parametry antény jako jsou vstupní impedance, zisk či směrová charakteristika.

Celý postup, který jsme zde shrnuli do bodů 1 až 5, je detailně popsán ve vrstvě B a v publikacích [10] a [11]. Nahradíme-li při tomto postupu všechny derivace středovými diferencemi, dojdeme k maticové rovnici

U_{x} = Z_{x x} I_{x}

( 4.4A.11 )

V této rovnici značí U_x sloupcový vektor napětí ve směru x na buňkách. Tato napětí vypočteme tak, že x-ovou složku vektoru elektrické intenzity násobíme x-ovým rozměrem diskretizační buňky

U_{x} (m, n) = E_{x} (m, n) a

( 4.4A.12 )

Symbol a značí výšku diskretizační buňky (tedy rozměr buňky ve směru x).

Jelikož předpokládáme, že náš mikropáskový dipól je vyroben z dokonale elektricky vodivého materiálu (a tudíž je napětí na tomto materiálu nulové), bude napěťový vektor sestávat (vyjma elementů odpovídajících budícím buňkám) ze samých nul.

Dále, I_x je sloupcový vektor proudů ve směru x. Tento vektor je pro nás v tuto chvíli neznámý. Prvky vektoru I_x jsou přitom se složkou vektoru proudové hustoty J_x svázán vztahem

I_{x} (m, n) = J_{x} (m, n) B

( 4.4A.13 )

(B je šířka dipólu, a tedy i diskretizační buňky). Impedanční matice Z_xx popisuje příspěvky proudů I_x a příspěvky nábojových hustot ρ (vyjádřených na základě rovnice kontinuity (4.4A.4) pomocí x-ových složek vektoru proudové hustoty J_x na buňkách) k napětím U_x na těchto buňkách. Jednotlivé prvky impedanční matice Z_xx přitom známe (viz vrstva B)

Z_{x x} (m, n) = \frac{j ω a}{B} Γ_{A}^{x x} (m, n) + \frac{1}{j ω a B} [Γ_{V} (m^{+}, n^{+}) - Γ_{V} (m^{-}, n^{+}) - Γ_{V} (m^{+}, n^{-}) + Γ_{V} (m^{-}, n^{-})]

(4.4A.14 )

K vyčíslení impedanční matice Z_xx potřebujeme znát hodnoty integrálů Greenových funkcí Γ_A^xx a Γ_V přes plochu diskretizační buňky pro různé vzdálenosti mezi buňkou zdrojovou (přes jejíž plochu integrujeme rozložení nábojů a proudů) a buňkou cílovou (na jejíž ploše počítáme elektrickou intenzitu). Popis numerického výpočtu těchto integrálů v Matlabu popisujeme ve vrstvě D.

Hotový matlabovský program, který pomocí popsané metody analyzuje náš mikropáskový dipól, popisujeme z uživatelského hlediska ve vrstvě C. Na tomto místě si tedy uvedeme pouze ilustrační výsledky, kterých bylo pomocí tohoto programu dosaženo.

Obr. 4.4A.3

Proudová distribuce na půlvlnném symetrickém mikropáskovém dipólu s rovinným reflektorem ve vzdálenosti rovné čtvrtině vlnové délky. Distribuce byla počítána pro 40 buněk.

Pro jednoduchost předpokládejme, že substrát mezi dipólem a reflektorem má parametry vakua. Je-li náš dipól stejně dlouhý jako polovina vlnové délky a je-li široký B = λ/1000, dostáváme následující vstupní impedance (v prvním řádku tabulky uvádíme počet diskretizačních buněk, na něž byla anténa rozdělena):

Tab. 4.4A.1

Vstupní impedance pro různý počet buněk

N	10	20	30	40
R_vst [Ω]	95.2	97.3	98.0	98.4
X_vst [Ω]	72.4	73.6	74.7	75.5

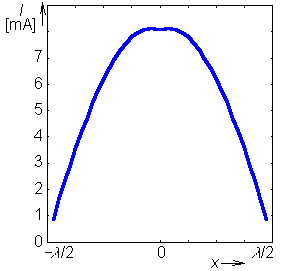
Z uvedených výsledků je vidět, že metoda vykazuje při změně počtu diskretizačních prvků celkem stabilní chování. A navíc, vstupní impedance našeho mikropáskového dipólu s reflektorem, vypočtená momentovou metodou, je velmi blízká výsledkům analytických výpočtů, předpokládajících sinusové rozložení proudu J_x na drátovém symetrickém dipólu s nekonečně rozlehlým reflektorem; pro drátový dipól dostáváme odpor záření antény vztažený k jejímu vstupu o hodnotě R_Σ = 85.6 Ω.

Pokud bychom se zajímali o aproximaci rozložení x-ové složky proudu podél mikropáskového dipólu, tu můžeme vykreslit vynesením aproximačních koeficientů z vektoru I_x do grafu. Dostali bychom tak průběh velmi blízký sinusovému rozložení proudu (viz obr. 4.4A.3).