4.4 Mikropáskový dipólPodrobnější popis
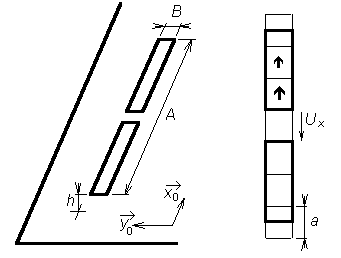
Termínem mikropáskový dipól budeme označovat anténu, která sestává ze dvou úzkých mikropáskových ramen, napájených uprostřed symetrickým zdrojem. Anténa je umístěna na lícní straně dielektrického substrátu. Dolní strana substrátu je zcela pokovena a má nulový potenciál (obr. 4.4B.1). Působení proudů tekoucích anténou můžeme popsat pomocí vektorového potenciálu
Působení nábojů na anténě popíšeme pomocí potenciálu skalárního
V uvedených vztazích značí A(r) vektorový potenciál v bodě r, J je vektor proudové hustoty v bodě r0, GA je dyadická Greenova funkce a GV Greenova funkce skalární (více viz vrstva D). Argumentem Greenových funkcí r|r0 naznačujeme, že právě počítáme příspěvek proudu (náboje) v bodě r0 k potenciálům v bodě r. Symbol ρ označuje nábojovou hustotu. Proudová a nábojová hustota na dipólu jsou vzájemně svázány rovnicí kontinuity
Máme-li vyjádřen jak vektorový tak skalární potenciál na ploše mikropáskového dipólu, můžeme vypočíst elektrickou intenzitu vlny, která je anténou vyzařována
Aplikací (4.4B.1) na mikropáskový dipól z obr. 4.4B.1 a dosazením z rovnice kontinuity do (4.4B.1b) dojdeme ke vztahům
V uvedených vztazích značí Ax x-ovou složku vektorového potenciálu a V je potenciál skalární, GAxx značí x-ový diagonální prvek dyadické Greenovy funkce a GV je Greenova funkce skalární, Jx je x-ová složka hledaného vektoru proudové distribuce a Ex je x-ová složka vektoru intenzity vyzařovaného elektrického pole. Podrobnosti čtenář nalezne ve vrstvě A. Dosazením vektorového potenciál (4.4B.2a) a skalárního potenciálu (4.4B.2b) do vztahu (4.4B.2c) dostáváme výchozí rovnici pro momentovou analýzu dipólu
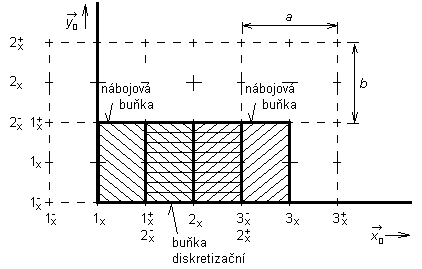
Velikost elektrické intenzity na ploše mikropáskového dipólu jsme schopni určit za předpokladu jeho dokonalé vodivosti z okrajové podmínky (vyjma napájecí štěrbiny musí být nulová). Jedinou neznámou ve vztahu (4.4B.3) je tudíž x-ová složka vektoru proudové hustoty Jx. V prvém kroku rozdělíme plochu dipólu na diskretizační buňky. Střed prvního diskretizačního prvku bude mít kótu 1, střed druhého prvku bude popsán kótou 2, atd. Horní hranici diskretizačního prvku označíme kótou se stejným číslem jako je kóta středu, avšak přidáme k tomuto číslu horní index "+" (plus). I dolní hranice diskretizačního prvku bude mít stejnou kótu jakou má střed, ale doplněna bude horním indexem "-" (mínus), viz obr. 4.4B.1. Dále se domluvme na tom, k čemu budeme jednotlivé různé body v diskretizační síti používat. Ve středech buněk budeme počítat velikost x-ové složky vektoru elektrické intenzity. Jelikož ve výpočtu příspěvků proudů k velikosti elektrické intenzity prostřednictvím složek vektorového potenciálu nevystupují žádné derivace (viz vztahy 4.4B.2), bude složka vektorového potenciálu počítána ve středech buněk. Naproti tomu při výpočtu příspěvků nábojů k elektrické intenzitě prostřednictvím skalárních potenciálů dvakrát derivujeme podle x, přičemž derivace v numerickém výpočtu nahrazujeme středovými diferencemi. Hodnoty skalárního potenciálu V, jehož derivováním počítáme příspěvky nábojů k elektrické intenzitě vyzařované vlny, tedy budeme muset znát na hranách diskretizačních buněk, aby výsledek středového diferencování ležel uprostřed diskretizační buňky. Ze vztahu pro výpočet skalárního potenciálu z nábojové hustoty pak ale vyplývá, že i hodnoty nábojové hustoty musíme znát na hranách diskretizačních buněk. Hodnoty nábojové hustoty budeme počítat z rovnice kontinuity derivováním složek proudové hustoty, přičemž derivace budou opět nahrazeny středovými diferencemi. Abychom dostali hodnoty nábojové hustoty na hranách diskretizačních buněk, musíme je počítat diferencováním složek proudové hustoty ve středech těchto buněk. Toto zjištění je pro nás velmi příjemné, neboť (jak jsme uvedli výše) platnost hodnot složek proudové hustoty jsme již dříve uvažovali právě v těchto bodech. Závěrem tedy můžeme shrnout, že hodnoty složek vektoru proudové hustoty musejí být počítány ve středech diskretizačních buněk a hodnoty hustoty nábojové na jejich hranách. Proto i hodnoty složek vektorového potenciálu a hodnoty složek vektoru elektrické intenzity musejí platit pro středy diskretizačních buněk a hodnoty potenciálu skalárního pro hrany buněk. Dalším krokem je dosazení po částech konstantní aproximace rozložení proudů do výchozích vztahů a náhrada všech parciálních derivací středovými diferencemi. Nejprve se přitom zaměřme na rovnici kontinuity, z níž vyjádříme nábojovou hustotu na horním a na dolním okraji diskretizační buňky
Symbol a značí výšku diskretizační buňky (viz obr. 4.4B.1), Jx(mx, nx) odpovídá konstantní hodnotě x-ové složky vektoru proudové hustoty na ploše buňky s kótou středu (mx, nx) a symbol ω je úhlový kmitočet. Na základě vztahů (4.4B.4a) a (4.4B.4b) budeme počítat příspěvek nábojů, reprezentovaných nábojovou hustotou ρ, k x-ové složce vektoru elektrické intenzity. Z hodnot nábojové hustoty na horním okraji diskretizačního prvku ρ(mx+, nx) a na okraji dolním ρ(mx-, nx) můžeme totiž vypočíst hodnoty skalárního potenciálu na těchto okrajích, a dále, náhradou parciální derivace skalárního potenciálu podle x středovou diferencí dostaneme příspěvek nábojů k x-ové složce vektoru elektrické intenzity. Nyní tedy známe hodnoty nábojových hustot na okrajích diskretizačních buněk. V dalším budeme ovšem předpokládat, že tyto hodnoty platí nejen na zmíněných okrajích, ale že jsou platné na celých plochách nábojových buněk, které mají stejný rozměr jako diskretizační buňky, avšak jsou posunuty tak, aby byly okraji diskretizačních buněk půleny (viz obr. 4.4B.1). Pak můžeme nábojové hustoty popsat následujícími po částech konstantními funkcemi
V těchto vztazích značí Π(xm+,yn | x,y) funkci, která nabývá jednotkové hodnoty na obdélníkové oblasti se středem v bodě (xm+, yn), se šířkou a a s výškou B (obdobně tomu je pro body (xm-, yn)). Hodnoty nábojové hustoty ρ (xm+, yn) a (xm-, yn) uprostřed této obdélníkové oblasti jsou přitom dány vztahy (4.4B.5). Pokud známe rozložení nábojové hustoty na mikropáskovém dipólu, můžeme z tohoto rozložení dosazením do vztahu vypočíst hodnoty skalárního potenciálu na příslušných nábojových buňkách. Pro nábojovou buňku, která je půlena horním okrajem buňky (mx, nx), tak dostáváme vztah
a obdobně pro V(mx-, nx).
Dříve, než půjdeme dále, zastavme se ještě na chvíli u vztahu (4.4B.6). Při jeho úpravě jsme zaměnili pořadí integrování a sčítání a integrál součinu jednotkového skoku Π se skalární Greenovou funkcí GV přes celý dipól jsme nahradili integrálem samotné skalární Greenovy funkce GV po ploše té nábojové buňky, na níž je funkce Π nenulová. Co se týká indexování, indexy (m, n) určují pozici cílové buňky, pro jejíž plochu počítáme hodnotu skalárního potenciálu, a indexy (p, q) specifikují pozici zdrojové buňky, jejíž náboje ke skalárnímu potenciálu buňky (m, n) přispívají. Jedinou spojitou funkcí v (4.4B.6) je skalární Greenova funkce GV, a proto pouze u této funkce musíme vyčíslit určitý integrál. Při vyčíslování tohoto integrálu pro různé vzdálenosti zdrojové buňky od buňky cílové přitom postupujeme tak, že pouze měníme pozici cílové buňky a zdrojovou buňku máme stále umístěnu v počátku; proto jsou integrační meze ve všech případech stejné (od -a/2 do +a/2 pro souřadnici x' a od -B/2 do +B/2 pro souřadnici y'). V tuto chvíli jsme tedy v situaci, že známe konstantní hodnoty skalárního potenciálu na plochách všech nábojových buněk. Proto můžeme postupovat dále tak, že středovým diferencováním těchto hodnot vypočteme příspěvky nábojů, reprezentovaných skalárním potenciálem, k hodnotám x-ové složky vektoru elektrické intenzity
Zde a značí výšku buňky, B je šířka buňky a hodnoty skalárního potenciálu V na plochách nábojových buněk jsou dány vztahem (4.4B.6). Jak jsme se zmínili již dříve, našim cílem je vyjádřit aproximaci elektrické intenzity vyzařované vlny na ploše dipólu jako funkci proudové hustoty na tomto dipólu. Proto musíme v prvém kroku za hodnoty skalárního potenciálu na okrajích buněk V dosadit z (4.4B.6), čímž se (4.4B.7) stane funkcí nábojové hustoty ρ na okrajích buněk
Ve výše uvedeném vztahu značí a výšku diskretizační buňky a B její šířku. Úhlový kmitočet ω odpovídá frekvenci, na níž anténu analyzujeme. Symbol VExS značí příspěvek skalárního potenciálu V k velikosti x-ové složky vektoru elektrické intenzity vyzařované vlny. A konečně ΓV reprezentuje integrál skalární Greenovy funkce GV na ploše buňky
V dalším kroku na naší cestě k vyjádření elektrické intenzity jako funkce proudové hustoty musíme do vztahu (4.4B.9) dosadit hodnoty nábojových hustot ze vztahů (4.4B.5)
Vztah vyjadřuje příspěvek nábojů ke složce vektoru elektrické intenzity pomocí neznámých hodnot složky vektoru proudové hustoty Jx a pomocí známých koeficientů ΓV, daných vztahem (4.4B.9). Z hlediska skalárních potenciálů jsme tedy dospěli k cíli, a proto se nyní věnujme potenciálu vektorovému. Abychom mohli vyčíslit příspěvky proudu k hodnotám elektrické intenzity, musíme vypočíst vektorový potenciál dosazením po částech konstantní aproximace proudové hustoty do vztahu (4.4B.2a)
Ve výše uvedeném vztahu značí
Dále, a je výška diskretizační buňky a B je její šířka. GAxx značí x-ovou diagonální složku dyadické Greenovy funkce. Funkce Π (px, qx| x',y') nabývá jednotkové hodnoty na buňce se středem v bodě (px, qx) a na ostatních buňkách je nulová. Hodnoty Jx reprezentují po částech konstantní proudové hustoty v síti buněk (px, qx). V právě uvedeném odvození jsme opět přehodili pořadí integrace a sčítání a integrál přes celou plochu dipólu S jsme nahradili integrálem přes plochu jediné buňky (protože v důsledku násobení funkcí Π je hodnota integrandu nenulová pouze na jediné diskretizační buňce). Konečně, dosazením vektorového potenciálu do vztahů (4.4B.3) a náhradou derivací skalárního potenciálu v těchto vztazích příspěvky (4.4B.10) dostáváme finální rovnici
Získaná rovnice (4.4B.13) je bohužel dosti nepřehledná. Abychom tuto nectnost odstranili, přepíšeme ji do maticové formy
V této rovnici značí Ux sloupcový vektor napětí ve směru x na buňkách. Tato napětí vypočteme tak, že x-ovou složku vektoru elektrické intenzity násobíme x-ovým rozměrem diskretizační buňky
Symbol a značí výšku diskretizační buňky (tedy rozměr buňky ve směru x). Jelikož předpokládáme, že náš mikropáskový dipól je vyroben z dokonale elektricky vodivého materiálu, bude napěťový vektor sestávat (vyjma budicích buněk) ze samých nul. Dále, Ix je sloupcový vektor neznámých proudů ve směru x. Prvky vektoru Ix jsou se složkou vektoru proudové hustoty Jx svázány vztahem
(B je šířka dipólu, a tedy i diskretizační buňky). Impedanční matice Zxx popisuje příspěvky proudů Ix a příspěvky nábojových hustot ρ k napětím Ux na buňkách. Jednotlivé prvky impedanční matice Zxx získáme srovnáním vztahů (4.4B.13) až (4.4B.16)
K vyčíslení impedanční matice Zxx potřebujeme znát hodnoty integrálů Greenových funkcí přes plochu diskretizační buňky pro různé vzdálenosti mezi buňkou zdrojovou a buňkou cílovou. Popis numerického výpočtu těchto integrálů v Matlabu popisujeme ve vrstvě D. Hotový matlabovský program, který pomocí popsané metody analyzuje mikropáskový dipól, popisujeme z uživatelského hlediska ve vrstvě C. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||