4.4 Microstrip dipole

Developing Matlab

Since we became familiar with theoretical basis of the moment analysis of the microstrip dipole in the layer A (and the layer B), we can turn our attention to the software implementation of the analysis in Matlab.

First, we take care for the numerical evaluation of integrals of Green functions.

For simplicity, we introduce a variable, which expresses the distance between the actual position of the source of waves (x’, y’) and the actual observation point (x_m,y_n) on the surface of the dipole

δ = \sqrt{{(x_{m} - x^{'})}^{2} + {(y_{n} - y^{'})}^{2}}

( 4.4D.1 )

Using the distance δ the x diagonal component of dyadic Green function is of the form [12]

G_{A}^{x x} (δ) = \frac{μ}{4 π} {\frac{\exp [- j k_{0} r_{0} (δ)]}{r_{0} (δ)} - \frac{\exp [- j k_{0} r_{1} (δ)]}{r_{1} (δ)}}

( 4.4D.2 )

where

k_{0} = ω \sqrt{μ_{0} ε_{0}}

( 4.4D.3 )

denotes wave-number in the vacuum (μ₀ and ε₀ are permeability and permittivity of the vacuum and ω is angular frequency of the wave we are working with). Next, distances r₀ and r₁ can be described by the relation

r_{i}^{2} (δ) = δ^{2} + {(2 i h)}^{2}

( 4.4D.4 )

where δ is the distance between the source and observation point on the surface of the antenna element and h is the height of the substrate.

Scalar Green function can be described by the following relation [12]

G_{V} (δ) = \frac{1 - η}{4 π ε} [\frac{\exp (- j k_{0} r_{0})}{r_{0}} - (1 + η) \sum_{i = 1}^{\infty} \frac{{(- η)}^{i - 1} \exp (- j k_{0} r_{i})}{r_{i}}]

( 4.4D.5 )

where

η = \frac{ε_{r} - 1}{ε_{r} + 1}

( 4.4D.6 )

and the rest of symbols is of the same meaning as described in layers A and B. Let us notice the infinite sum in the relation (4.4D.5). If the dielectrics between the ground plane and the microstrip dipole is replaced by the vacuum, the sum consists of a single non-zero summand (substituting ε_r = 1 to (4.4D.6) yields η = 0, and only the zero power of zero differs from zero). Increasing the value of the permittivity, the coefficient h approaches one, and the value of summands decreases relatively slowly (the decrease is caused by the increasing value of r_i). Therefore, the number of summands has to be increased when relative permittivity rises. The following table illustrates the situation:

Tab. 4.4D.1

Number of summands for different permittivity values

ε_r	2	4	6	9
i	9	16	23	33

Here, i denotes an index of the second addend in the summation (4.4D.5), which modulus is lower than 0.01 (considered parameters: f = 3 GHz, δ = 0 mm, h = 1.5 mm)

Green functions (4.4D.2) and (4.4D.5) are not of general validity. They can be used for a microstrip structure consisting of a ground plane, of a homogeneous dielectric substrate and of a microstrip antenna element only. Moreover, those relations can be utilized for a very low distance between sources of EM field and observation points, where electric field intensity is computed. Since we compute electric field intensity on the surface of the microstrip antenna element, the distance between sources and observation points is satisfactorily short for exploiting (4.4D.2) and (4.4D.5).

Now, when mathematic description of Green functions is known to us, we can start their integration over the whole surface of a discretization element. Since analytic solution of those integrals is unknown, we perform that in a numeric way. The numeric integration does not cause any problems if the source element differs from the destination one. In the opposite case (when computing contributions of currents and charges on the element to the electric field intensity on the same element), the problem of singularity of the integrated function appears. If the source point and the destination one are identical then their distance δ is zero (4.4D.1). As obvious from (4.4D.4), even the distance r₀, which is present in the denominators of Green functions (4.4D.2) and (4.4D.5), is zero. As explained in [13], the singularity is weak, and therefore, we can eliminate it. The singularity elimination consists in dividing Green function G to the singular part G_H (which has to be carefully handled) and to the regular one (G - G_H), which can be numerically integrated a usual way. Hence

G = G_{H} + (G - G_{H})

( 4.4D.7 )

In our case, only the first term of Green functions (4.4D.2) and (4.4D.5) is singular. On the basis of (4.4D.7), the singular term can be divided to the singular part and to the regular one by the following way:

\frac{\exp (- j k_{0} r_{0})}{r_{0}} = \frac{1}{r_{0}} + \frac{\exp (- j k_{0} r_{0}) - 1}{r_{0}}

( 4.4D.8 )

Whereas the singular part of Green function is represented by the first addend in (4.4D.8), the second addend in (4.4D.8) corresponds to the regular difference of Green functions. Regularity of the second addend can be proven by computing its limit for the distance between the source and observation point tending to zero

\lim_{r_{0} \to 0} \frac{\exp (- j k_{0} r_{0}) - 1}{r_{0}} = \lim_{r_{0} \to 0} \frac{- j k_{0} \exp (- j k_{0} r_{0})}{1} = - j k_{0}

( 4.4D.9 )

Evaluating this limit, l'Hospital rule was used.

The integral of the singular part of Green function over the whole surface of the discretization element can be computed analytically [12]

\int_{- a / 2}^{+ a / 2} \int_{- B / 2}^{+ B / 2} \frac{d x d y}{\sqrt{x^{2} + y^{2}}} ≅ 2 a \ln [\tan (\frac{α}{2} + \frac{π}{4})] - 2 b \ln [\tan (\frac{α}{2})]

( 4.4D.10 )

Here, a denotes the height of the discretization element, b is its width and a is given by

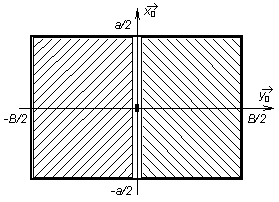
Fig. 4.4D.1

Integrating singular parts of Green function over discretization cell

t g α = \frac{B}{a}

( 4.4D.11 )

The practical algorithm of computing the singular term of Green functions (4.4D.2) and (4.4D.5) is illustrated by fig. (4.4D.1). The regular part of the singular term (the second addend in eqn. 4.4D.8) is numerically integrated from -a/2 to a/2 with respect to x and from -B/2 to -n with respect to y (see the left-hand part of the element). The number n approaches zero (-10^-5, e.g.), which enables us to integrate up to a near distance from the origin (here, the integration is troubled by zero denominator). Since the integrated function behaves well near the origin (as shown in eqn. (4.4D.9), its value is about jk₀ here), only a small inaccuracy is produced.

The integral of the regular part of the singular Green function over the right-hand part of the element does not need to be evaluated because its numerical value is the same as the left-hand side integral.

The complete integral of Green function is computed by taking twice the left-hand side integral and by adding the integral of the singular term, which is obtained by evaluating (4.4D.10).

Now, the moment analysis can be implemented in Matlab.

Programming the moment method, we start to write m-files containing Green function. Therefore, we have to write m-files implementing relations (4.4D.2) and (4.4D.5).

The first m-file of Green function is devoted to the case when computing contribution of charges and currents on the discretization element to potentials on the same element. Moreover, we concentrate to the term, where the distance r₀ is present (we compute effects of currents on the antenna element to observation points on the same element). Performing the described integration, singularity appears.

r0 = sqrt( x.*x + y^2);
out = ( exp( -j*k0*r0) - 1)./r0;

The second file of Green function is used to computing contributions of charges and currents on the discretization element to potentials on other elements (i.e., terms containing r₀ for non-zero distance between sources and observation points are handled) and to computing effects of the ground plane (i.e., terms containing r_i are handled). Therefore, singularity does not appear when integrating.

r1 = sqrt( (x+xdis).*(x+xdis) + y^2 + (2*i*h)^2); out = exp( -j*k0*r1)./r1;

In the above-given source code, x and y denote the position of a source. Sources are assumed on an element, which center corresponds to the origin of the coordinate system (0, 0). The distance between the center of the observation element and the center of the source element in x-direction is given by the parameter xdis. The parameter h denotes the distance between the dipole and the reflector, and k0 is wave-number in vacuum (where the antenna is placed).

Integrating Green function, parameters x and y vary over the whole surface of the observation element. Parameters xdis, h and k0 are constant during integration. Nevertheless values of constant parameters have to be passed on m-files of Green functions. Passing on is implemented by declaring xdis, h and k0 as global variables. Then, content of these variables is visible from any m-file of the program. Global variables are declared by typing

global h k0 xdis i

both at the beginning of the main m-file and at the beginning of all m-files, which exploit these variables.

Finally, integration variables x and y are passed on m-files as parameters in their headers:

function out = regular( x, y)

Now, Green functions are ready to integration over the whole surface of the element, and therefore, the main m-file can be written. After initial declarations (determining frequency, antenna dimensions, and the discretization mesh), a cycle over all the possible distances of discretization elements is programmed. For each distance, we evaluate integrals of Green functions and we store them to the array psi. The first index of psi indicates the distance between the source element and the observation one in x-direction, the second index can be up to the value Ne (integral of the term of Green function, which contains the distance r_n). The whole cycle can be of the following form:

psi = zeros( Nx+2, Ne);
for m=1:(Nx+2)

xdis = (m-1)*a; % horizontal distance of element centers
if m==1

psi(m,1) = 2*dblquad('singular', -a/2, +a/2, 1e-10, B/2, 1e-3, 'quad');
psi(m,1) = psi(m,1) + stt;

else

i = 0;
psi(m,1) = dblquad('regular', -a/2, +a/2, -B/2, B/2, 1e-3, 'quad');

end
for i=1:Ne

psi(m,i+1) = dblquad('regular', -a/2, +a/2, -B/2, B/2, 1e-3, 'quad');

end

The above-given source code shows that the singular function is integrated in such a case only, when the source discretization element and the observation one are identical (m = 1) and when the effect of the reflector is not handled.

As already explained, the singular Green function is numerically integrated up to the close distance of the singularity (i.e., up to the distance 10^-10 meters), and then, the value of the analytically computed integral of the singular part (4.4D.10) is added

alp = atan( b/a);
stt = 2*a*log( tan( alp/2+pi/4)) - 2*b*log( tan( alp/2));

The double integral is numerically evaluated using the standard Matlab function dblquad. The first parameter is the string containing the name of the m-file, where he integrated function is implemented. Integration limits of the first integration variable are the second parameter and the third one (the variable has to be the first parameter in the header of the m-file containing the integrated function). Integration limits of the second integration variable are the fourth parameter and the fifth one (the variable has to be the second parameter in the header of the m-file containing the integrated function).

The sixth parameter of dblquad can be used for determining accuracy of numeric integration, and the last parameter can specify the algorithm of numeric integration.

When integrals of Green functions are evaluated for all the possible distances between elements, the impedance matrix Z_xx (4.4A.14, 4.4B.17) can be composed. Composing can be performed by the following source code:

G = ( psi(:,1) - psi(:,2))/(4*pi);
cf1 = (1-eta)/(j*omg*ep0*epr*a*B);
cf2 = j*omg*mi0*a/B;

% relation betw. currents and voltages

ix = 0;
Zxx = zeros( Nx, Nx);

for m=1:Nx % over observation elements in x

ix = ix + 1; iy = 0;
for o=1:Nx % over source elements in x

dx = abs( m-o); % distance source - observation
iy = iy + 1;
hlp = 2*psi( 1+dx,1) - psi( 1+abs(dx+1),1) - psi( 1+abs(dx-1), 1);
for i=1:Ne

inc = ( 2*psi(1+dx,i+1)-psi(1+abs(dx+1),i+1)-psi(1+abs(dx-1),i+1)); hlp = hlp - (1+eta)*(-eta)^(i-1)*inc;

end
Zxx(ix,iy) = cf1*hlp/(4*pi) + cf2*G(1+dx,1);

end

The source code corresponds to relations (4.4A.14) and (4.4B.17).

Inverting the impedance matrix, admitance matrix is obtained. If excitation voltage 1 V is assumed, elements of the admitance matrix directly equal to currents on the microstrip dipole. Inverting the element of the admitance matrix, which corresponds to the excitation element, input impedance of the antenna is obtained.