4.4 Mikropáskový dipólVývoj programuNyní, když jsme se ve vrstvě A (a případně ve vrstvě B) seznámili s teoretickými základy analýzy mikropáskového dipólu momentovou metodou, můžeme se zabývat detaily implementace analýzy v Matlabu. V prvém kroku se podívejme na způsob, jakým lze numericky vyčíslit hodnoty integrálů Greenových funkcí. Pro zjednodušení zápisu si zaveďme proměnnou, která bude symbolizovat vzdálenost na ploše dipólu mezi aktuální polohou zdroje vlnění (x’, y’) a aktuální polohou bodu pozorování (xm, yn)
S využitím právě zavedené vzdálenosti δ pak můžeme x-ovou diagonální složku dyadické Greenovy funkce vyjádřit rovnicí [12]
kde
značí vlnové číslo ve vakuu (μ0 a ε0 jsou permeabilita a permitivita vakua a ω je úhlový kmitočet vlny, s níž pracujeme). Dále, vzdálenosti r0 a r1 můžeme společně vyjádřit vztahem
v němž δ je vzdálenost zdroje a bodu pozorování na ploše anténního prvku a h je výška substrátu, z něhož je anténa vyrobena. Skalární Greenovu funkci je možno vyjádřit následujícím vztahem [12]
kde
a zbytek symbolů má stejný význam, jak bylo uvedeno ve vrstvách A a B. Proto upozorněme pouze na sumu přes nekonečný počet sčítanců, která vystupuje ve vztahu (4.4D.5). Je-li dielektrikum mezi zemní deskou a mikropáskovým anténním prvkem nahrazeno vakuem, v sumě budeme mít jediný nenulový sčítanec (dosazením za εr = 1 do (4.4D.6) dostáváme η = 0 a pouze nulová mocnina nuly je od nuly různá). Pokud však budeme hodnotu permitivity substrátu zvyšovat, bude se koeficient η blížit jedničce. Potom hodnota sčítanců v sumě klesá relativně pomalu (pokles je způsoben pouze růstem hodnoty ri), a proto musíme se vzrůstající hodnotou relativní permitivity substrátu zvyšovat počet sčítanců v sumě. Popsaná situace je ilustrována tabulkou:
Zde i značí index druhého sčítance v sumě (4.4D.5), jehož modul je menší nežli 0.01 (uvažované parametry: f = 3 GHz, δ = 0 mm, h = 1.5 mm) Greenovy funkce (4.4D.2) a (4.4D.5) nemají bohužel obecnou platnost. Tyto vztahy jednak platí pouze pro mikropáskovou strukturu sestávající ze zemní desky, z homogenního dielektrického substrátu a z mikropáskového anténního elementu, a jednak je možno použít tyto vztahy jen pro velmi malou vzdálenost mezi zdroji elektromagnetického pole a mezi body, v nichž počítáme vektor elektrické intenzity. Jelikož my počítáme elektrickou intenzitu pouze na ploše mikropáskového anténního prvku, je vzdálenost mezi zdroji a cíli dostatečně malá, aby bylo možno vztahy (4.4D.2) a (4.4D.5) použít. Nyní, když známe matematický popis Greenových funkcí, vystupujících v našich vztazích, můžeme se pustit do jejich integrování přes celou plochu diskretizační buňky. A jelikož analytické řešení těchto integrálů není známo, budeme muset integrování provést numericky. Při numerickém integrování nedochází k žádným potížím v případě, kdy je zdrojová buňka odlišná od buňky cílové. V opačném případě (tj. když počítáme příspěvky proudů a nábojů na buňce k elektrické intenzitě na ploše téže buňky) však narazíme na problém singularity integrované funkce. Jsou-li totiž zdrojový a cílový bod totožné, je jejich vzdálenost δ nulová (4.4D.1). A jak vyplývá z (4.4D.4), potom i vzdálenost r0, která vystupuje ve jmenovatelích Greenových funkcí (4.4D.2) a (4.4D.5), nabývá nulové hodnoty. Jak je však popsáno v [13], jedná se o tzv. slabou singularitu (weak singularity), kterou je možno eliminovat. Eliminace singularity přitom spočívá v rozdělení Greenovy funkce G na singulární část GH (té je třeba věnovat speciální pozornost) a na část regulární (G - GH), k jejíž integraci je možno použít běžných algoritmů numerického integrování. Tedy
V našem případě je singulární pouze první člen v Greenových funkcích (4.4D.2) a (4.4D.5). Tento singulární člen můžeme přitom na základě (4.4D.7) rozdělit na singulární a regulární část následujícím způsobem
Zatímco singulární část Greenovy funkce je reprezentován prvním sčítancem v (4.4D.8), regulárnímu rozdílu Greenových funkcí odpovídá druhý sčítanec v (4.4D.8). O regularitě tohoto druhého sčítance se přitom můžeme přesvědčit výpočtem jeho limity pro případ, kdy vzdálenost mezi zdrojem a cílem konverguje k nule
Při výpočtu limity jsme použili l'Hospitalova pravidla. Integrál singulární části Greenovy funkce přes celou plochu diskretizační buňky lze vypočíst analyticky [12]
V tomto vztahu značí a výšku diskretizační buňky, b je její šířka a parametr α je dán vztahem
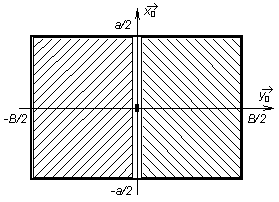
Praktický postup výpočtu singulárního členu v Greenových funkcích (4.4D.2) a (4.4D.5) je ilustrován obrázkem (4.4D.1). Regulární část singulárního členu (druhý sčítanec ve vztahu 4.4D.8) numericky integrujeme od -a/2 do a/2 podle x a od -B/2 do -ν podle y (viz levá vyšrafovaná oblast buňky). Číslo ν je velmi blízké nule (např. -10-5), takže se při numerické integraci přiblížíme na hodně malou vzdálenost ke středu, v němž by měla numerická integrace potíže s nulovým jmenovatelem. Jelikož se však integrovaná funkce v okolí středu chová velmi dobře (jak bylo ukázáno ve vztahu (4.4D.9), její hodnota se zde pohybuje okolo hodnoty jk0), dopustíme se tím pouze nepatrné chyby vzhledem k integraci v mezích <-B/2; 0>. Co se týká integrálu regulární části singulární Greenovy funkce přes pravou polovinu buňky, ten vyčíslovat nemusíme. Dá se totiž snadno ukázat, že jeho hodnota je stejná jako hodnota integrálu přes levou polovinu buňky. Celý integrál Greenovy funkce tudíž vypočteme tak, že integrál regulární části přes polovinu buňky vynásobíme dvěma a k tomuto násobku připočteme integrál části singulární, který získáme vyčíslením vztahu (4.4D.10). V tuto chvíli máme tudíž připraveno vše potřebné k tomu, abychom momentovou analýzu implementovali v Matlabu. Při programování momentové metody je vhodné začít psaním m-souborů s Greenovou funkcí. To znamená, že musíme napsat m-soubory, obsahující funkce definované vztahy (4.4D.2) a (4.4D.5). První soubor s Greenovou funkcí bude věnován případu, kdy počítáme příspěvek napětí a proudů na diskretizačním prvku k potenciálům na tomtéž prvku, a zároveň se omezujeme na člen, ve kterém vystupuje vzdálenost r0 (počítáme vliv zdrojů na anténním prvku k cílům na tomtéž prvku). Při integraci této funkce se objevuje singularita
r0 = sqrt( x.*x + y^2);
out = ( exp( -j*k0*r0) - 1)./r0; Druhý soubor s Greenovou funkcí pak využijeme k výpočtu příspěvků napětí a proudů na diskretizačním prvku k potenciálům na jiném prvku (tím myslíme členy s r0 pro nenulovou vzdálenost mezi zdroji a cíli) a k výpočtu vlivu zemní desky (tím myslíme členy, ve kterých vystupují vzdálenosti ri), takže singularita se při jejich integrování neobjeví
r1 = sqrt( (x+xdis).*(x+xdis) + y^2 + (2*i*h)^2);
out = exp( -j*k0*r1)./r1; V uvedených zdrojových textech značí x a y polohu zdroje. Zdroje vždy leží na buňce, jejíž střed odpovídá počátku souřadné soustavy (0, 0). Vzdálenost středu cílové buňky od středu buňky zdrojové ve směru x je dána parametrem xdis. Parametr h udává vzdálenost dipólu od reflektoru a k0 je vlnové číslo ve vakuu (v němž se nachází naše anténa). Při integraci Greenových funkcí budeme měnit parametry x a y přes celou plochu cílové buňky. Parametry xdis, h a k0 jsou během integrace konstantní. Hodnotu těchto konstantních parametrů však musíme m-souborům s Greenovými funkcemi nějak předat. Nejsnadnější předání jejich hodnot zabezpečíme tak, že budeme uvedené parametry deklarovat jako globální proměnné. Potom bude obsah těchto proměnných viditelný ze všech m-souborů našeho programu, aniž bychom jej museli m-souborům předávat prostřednictvím vstupních parametrů v jejich hlavičkách. Globální charakter uvedených proměnných naprogramujeme v matlabu tak, že jak na začátku hlavního m-souboru (o něm bude řeč za chvíli) tak na začátcích m-souborů s Greenovými funkcemi uvedeme
global h k0 xdis i
Potom nám stačí v hlavičkách m-souborů s Greenovými funkcemi udávat pouze integrační proměnné x a y, např.
function out = regular(x, y)
Nyní tedy máme Greenovy funkce připraveny k integraci po celé ploše diskretizační buňky, a proto můžeme začít psát hlavní m-soubor našeho programu. Po úvodních deklaracích, v nichž zadáme kmitočet, na němž bude analýza probíhat, a v nichž určíme rozměry antény a architekturu diskretizační sítě, začneme psát cyklus přes všechny možné vzdálenosti diskretizačních prvků. Pro každou z těchto vzdáleností pak budeme počítat integrály Greenových funkcí a získané hodnoty budeme ukládat do pole psi. První index pole psi bude udávat vzdálenost zdrojové a cílové buňky ve směru x, druhý index nabývá hodnoty Ne (integrál členu Greenovy funkce, obsahující vzdálenost rn). Celý cyklus by tudíž mohl vypadat takto:
psi = zeros( Nx+2, Ne);
for m=1:(Nx+2)
xdis = (m-1)*a; % vodorovná vzdálenost středů buněk
end
if m==1
psi(m,1) = 2*dblquad('singular', -a/2, +a/2, 1e-10, B/2, 1e-3, 'quad');
else
psi(m,1) = psi(m,1) + stt;
i = 0;
endpsi(m,1) = dblquad('regular', -a/2, +a/2, -B/2, B/2, 1e-3, 'quad'); for i=1:Ne
psi(m,i+1) = dblquad('regular', -a/2, +a/2, -B/2, B/2, 1e-3, 'quad');
end
Z uvedeného zdrojového kódu je vidět, že k integraci singulární funkce dochází jen v tom případě, kdy zdrojový a cílový diskretizační prvek splývají (m = 1) a kdy počítáme vliv anténního prvku na potenciály na tomtéž prvku (nepočítáme vliv reflektoru). Jak jsme již popsali výše, singulární Greenovu funkci numericky integrujeme do těsné blízkosti singularity (tj. do vzdálenosti 10-10 metrů), a poté k ní připočteme hodnotu analyticky vypočteného integrálu singulární části (4.4D.10)
alp = atan( b/a);
stt = 2*a*log( tan( alp/2+pi/4)) - 2*b*log( tan( alp/2)); K samotnému numerickému výpočtu dvojného integrálu používáme standardní matlabovskou funkci dblquad. Prvním parametrem této funkce je textový řetězec se jménem m-souboru, v němž je uložen integrand. Druhým a třetím parametrem jsou integrační meze pro první integrační proměnnou (ta musí být uvedena jako první parametr v hlavičce m-souboru s integrandem), čtvrtý a pátý parametr musejí obsahovat integrační meze druhé integrační proměnné (druhý parametr v hlavičce m-souboru s integrandem). Kromě uvedených dvou parametrů nesmějí m-soubory s integrandem obsahovat ve své hlavičce žádné další vstupní údaje, a proto jsme další potřebné parametry předávali prostřednictvím globálních proměnných. Prostřednictvím šestého parametru funkce dblquad zadáváme požadovanou přesnost numerické integrace a prostřednictvím parametru posledního pak jméno algoritmu, který má být k numerické integraci použit. Pokud máme vyčísleny integrandy Greenových funkcí pro všechny možné vzdálenosti mezi zdroji a cíli, můžeme začíst sestavovat impedanční matici Zxx (4.4A.14, 4.4B.17). Sestavení impedanční matice pak může být realizováno následujícím zdrojovým kódem:
G = ( psi(:,1) - psi(:,2))/(4*pi);
cf1 = (1-eta)/(j*omg*ep0*epr*a*B); cf2 = j*omg*mi0*a/B; % vztah mezi proudy a napětími ix = 0; Zxx = zeros( Nx, Nx); for m=1:Nx % přes cílové buňky ve směru x
ix = ix + 1;
end
iy = 0; for o=1:Nx % přes zdrojové buňky ve směru x
dx = abs( m-o); % vzdálenost cílové a zdrojové buňky
end
iy = iy + 1; hlp = 2*psi( 1+dx,1) - psi( 1+abs(dx+1),1) - psi( 1+abs(dx-1), 1); for i=1:Ne
inc = ( 2*psi(1+dx,i+1)-psi(1+abs(dx+1),i+1)-psi(1+abs(dx-1),i+1));
endhlp = hlp - (1+eta)*(-eta)^(i-1)*inc; Zxx(ix,iy) = cf1*hlp/(4*pi) + cf2*G(1+dx,1); Uvedený zdrojový kód zcela odpovídá vztahům (4.4A.14), resp. (4.4B.17), a proto je zbytečné jej podrobněji rozebírat. Konečně v posledním kroku určíme pomocí inverze impedanční matice matici admitanční. A jelikož jsme uvažovali napájení antény napětím 1 Volt, budou prvky admitační matice přímo rovny proudům na mikropáskovém dipólu. Převrácením admitance, která odpovídá napájecímu diskretizačnímu prvku, dostáváme vstupní impedanci antény. |