4.5 Flíčková anténa

Základní teorie

S mikropáskovou anténou (flíčkovou anténou) jsme měli možnost seznámit se již v článku o mikropáskovém dipólu (čl. 4.4). Nicméně, brzy jsme od této antény utekli a věnovali se dále využití jednorozměrné momentové metody na analýzu dipólu. Jelikož dvojrozměrná mikropásková anténa hraje v dnešních systémech bezdrátové komunikace velmi důležitou úlohu, v tomto článku se k ní vracíme.

V úvodní části popisujeme uspořádání mikropáskových antén a jejich vlastnosti. Poté se zabýváme analýzou těchto antén dvěma různými technikami. Závěrem srovnáváme přesnost a výpočetní náročnost uvedených postupů. V dodatku uvádíme přehled a základní vlastnosti komerčních programů pro analýzu mikropáskových antén.

I. Úvod

První zmínky o mikropáskových anténách se v literatuře začaly objevovat počátkem 50. let minulého století. Tehdy totiž začala vznikat potřeba vyrobit plošné antény, které by dobře kopírovaly povrch letadel a jiné vojenské techniky. Až později došlo k rozšíření aplikací do oblasti civilní, a to zejména do oblasti komunikací.

a)	b)
Obr. 4.5A.1 Klasická mikropásková anténa. a) štěrbinová mikropásková anténa b) napájecí vedení na dolní straně spodního substrátu vyznačeno červeně, štěrbiny v zemní desce zeleně

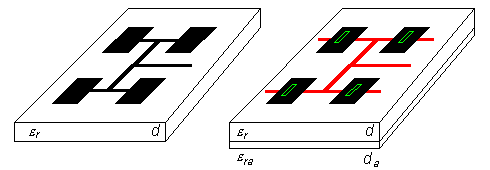
V současné době existuje celá řada různých typů mikropáskových antén. Tyto antény se od sebe odlišují tvarem anténního prvku (obdélníkový, kruhový), polarizací, s níž jsou schopny pracovat, způsobem napájení (v čl. 4.4 jsme poznali napájení mikropáskové a koaxiální), atd. My budeme v rámci tohoto článku pracovat s obdélníkovými mikropáskovými anténami, které jsou napájeny mikropáskovým vedením. Antény si rozdělíme do dvou skupin podle toho, zda je napájecí mikropásek umístěn na téže straně substrátu jako anténní prvky (klasická mikropásková anténa, obr. 4.5A.1a) či nikoli. Na druhý (novější) přístup k napájení se podívejme podrobněji.

Mikropáskové anténní zářiče jsou buzeny prostřednictvím štěrbin v zemní ploše. Vlastní napájecí vedení se pak nachází na substrátu, který je umístěný pod substrátem s anténou. Spodní substrát má s horním substrátem společnou zemní plochu se štěrbinou, na lícní (tedy dolní) straně spodního substrátu je pak vytvořeno samotné napájecí vedení (obr. 4.5A.1). Tuto skupinu antén budeme pro jednoduchost nazývat mikropáskovými anténami se štěrbinovým buzením.

Obě skupiny antén mají řadu společných vlastností a řadu odlišností (viz tab. 4.4A.1).

Společnou vlastností je velmi malá impedanční šířka pásma. Ta se u klasických mikropáskových antén pohybuje jen okolo 2 až 3% a u mikropáskových antén se štěrbinovým buzením okolo 4 až 6%. Důvodem malé šířky pásma je vysoký činitel jakosti běžně používaných zářičů. Ty se totiž chovají jako rezonátory s činitelem jakosti v řádu několika desítek.

Dalším sledovaným parametrem je účinnost antény. Účinnost vyzařování (počítá se pro případ bezeztrátové antény) je dána poměrem výkonu vyzářeného anténou (získá se integrací Poyntingova vektoru v blízké či vzdálené oblasti přes celý poloprostor) a činného výkonu na napájecí svorce zářiče (antény).

Energie, která není anténou vyzářena, je odvedena formou povrchových vln po nekonečně rozlehlém dielektrickém substrátu (i když ve skutečnosti je substrát pochopitelně omezen).

Prakticky je však zajímavá účinnost celková. Na ní se podílí kromě ztrát povrchovými vlnami také ztráty v dielektriku a ztráty, dané stojatými vlnami v substrátu (u substrátu s konečnými rozměry dochází k interferenci povrchových vln, které na okraj substrátu dopadají, s vlnami, které se od okrajů substrátu odrážejí). Celková účinnost mikropáskových antén je asi o 1 až 2 decibely horší nežli účinnost antén reflektorových.

Mikropáskové antény dále vynikají velmi dobrou úrovní křížové polarizace. U mikropáskových antén pracujících pouze s lineární polarizací není většinou tato vlastnost příliš zajímavá. Nabude však na důležitosti, pokud se snažíme navrhnout duální anténu s vysokou polarizační izolací.

II. Analýza osamoceného anténního zářiče

K analýze samotného anténního prvku lze v současnosti využít relativně mnoho rozdílných metod. My se však zmíníme pouze o třech nejčastěji používaných metodách, přičemž dvě z nich budou probrány podrobně.

Jeden z relativně jednoduchých způsobů analýzy mikropáskových antén připodobňuje anténní zářič k širokému mikropáskovému vedení, u něhož jsou za zdroj vyzařování považována okrajová elektrická pole (obr. 4.5A.2a).

Druhý způsob analýzy spočívá v náhradě prostoru pod zářičem ztrátovým rezonátorem. Pak totiž můžeme využít k výpočtu vstupní impedance antény teorii kvádrových dutinových rezonátorů [14].

Třetím způsobem analýzy pak je numerická analýza anténního zářiče metodou momentů, formulovaná ve spektrální oblasti nebo v oblasti prostorové (s takto formulovanou metodou jsme se již setkali v čl. 4.1, čl. 4.3 a čl. 4.4). V této kapitole se soustředíme na případ metody momentů v prostorové oblasti.

a)	b)	c)	d)
Obr. 4.5A.2 Analýza osamoceného zářiče (horní a spodní stěna jsou dokonale elektricky vodivé, okolní stěny jsou dokonale magneticky vodivé). a) metoda vedení   b) dutinový rezonátor   c) momentová metoda (malé bázové funkce)   d) náhradní model

II.I. Analýza osamoceného zářiče metodou vedení

Metoda vedení vyniká jednoduchostí, a přitom umožňuje dosáhnout i poměrně přesných výsledků. Přesnost, s jakou můžeme vypočíst vstupní impedanci zářiče, závisí na volbě modelu zářiče. V tomto odstavci budeme pracovat s nejjednodušším modelem, který uvažuje pouze zářící štěrbiny mezi dvěma sousedním mikropáskovými anténním prvky (tečná okrajová elektrická pole jsou považována za jediný zdroj záření). Další efekty jako vzájemné vazby mezi zdroji záření či záření zbylých dvou hran zanedbáváme.

Nejprve analyticky odvodíme vztah pro admitanci Y_S jedné štěrbiny mezi dvěma zářiči (výsledek přebíráme ze [14], kde se lze rovněž dobrat vlastního odvození)

Zde značí W délku štěrbiny [m], w je šířka štěrbiny [m] (je přibližně rovna výšce substrátu d), λ₀ značí délku vlny ve volném prostoru [m], k₀ je konstanta šíření ve volném prostoru (k₀ = 2π/λ₀) [m^-1] a Z₀ je impedance volného prostoru [Ω].

Ve vztahu se neobjevuje vliv permitivity substrátu, neboť předpokládáme konstantní velikost elektrické intenzity po celé délce štěrbiny.

Nyní můžeme přistoupit k návrhu vlastní antény. Délka zářiče se volí asi (0.48 ÷ 0.49) λ/2, kde λ = c / [f (ε_eff)^1/2 ] a kde efektivní permitivitu substrátu ε_eff stanovíme buď na základě kvazi-statických vztahů nebo numericky (při výpočtu efektivních permitivit či charakteristické impedance mikropáskového vedení je nutné vybrat vhodný typ kalkulátoru, neboť ne všechny správně modelují disperzi vedení na vyšších kmitočtech; vhodný je například Txline od AWR, resp. TRL85 v balíku Serenade 8.5SV).

Délka zářiče nemůže být přesně rovna polovině délky vlny, neboť přibližně půlvlnný úsek musí kapacitní impedanci pravé štěrbiny transformovat na impedanci induktivní, aby došlo ke vzájemné kompenzaci induktivní impedance s kapacitní impedancí první štěrbiny právě na kmitočtu f, na kterém anténu navrhujeme.

Druhý krok návrhu spočívá v takové volbě šířky zářiče W, která zaručí požadovanou hodnotu rezonančního odporu zářiče. Tento odpor můžeme vyjádřit jako R_rez = (2 G_S)^-1, kde G_S je reálná část admitance štěrbiny.

Po dosazení za vlnovou délku λ₀ a za charakteristickou impedanci mikropáskového vedení Z₀ dostaneme

Zvolíme-li W = λ₀/2, dostaneme rezonanční odpor roven právě 120 Ω.

Popsaný model anténního zářiče je platný pouze pro elektricky tenký substrát (tj. musí platit d / λ ≈ 0.01, kde d značí výšku substrátu).

Pokud požadujeme, aby byl rezonanční odpor větší jak 120 Ω, musí být délka zářiče W menší než polovina vlnové délky. Rezonanční odpor však nelze příliš zvětšovat, protože maximální hodnota odporu záření může být (s ohledem na realizovatelnost napájecího mikropáskového vedení) nejvýše 150 Ω. Pokud se rozhodneme připojit na vstup zářiče impedanční transformátor, lze navrhnout zářič s impedancí asi 240 Ω.

Postupovat při návrhu šířky zářiče opačným způsobem (tj. prodlužovat šířku anténního prvku) je krajně nevhodné z prostorových i funkčních důvodů (mohou se objevit parazitní rezonance a parazitní laloky).

V praxi se pro dosažení potřebně malého odporu záření používá místo napájení na hraně anténního prvku napájení blíže jeho středu.

Příklad návrhu jednoho anténního zářiče pomocí popsané metody uvádíme spolu s uživatelským popisem odpovídajícího matlabovského programu ve vrstvě C.

II.II. Analýza osamoceného zářiče metodou vedení

Výrazná nevýhoda metody vedení spočívá v tom, že ji lze použít jen pro omezený počet tvarů anténního zářiče a jen pro elektricky tenké substráty. Aby bylo možné analyzovat elementy obecnějšího tvaru a elementy na elektricky tlustých substrátech, je nutné použít numerické postupy založené na metodě momentů.

Budeme předpokládat, že máme planární anténní zářič (oproti čl. 4.4 dvojrozměrný), který je buzen mikropáskovým vedením. Cílem je spočítat vstupní impedanci antény v místě mikropáskového vstupu.

Obr. 4.5A.3 Síť nábojových a proudových buněk

Na anténním prvku existuje určité rozložení náboje a proudu (ve skutečnosti jde o proudovou hustotu; pro zkrácení budeme používat pojem proud). Abychom mohli spočítat vstupní impedanci, musíme nejprve určit tyto proudy a náboje. Poté bude možné vypočítat libovolnou další veličinu (např. intenzitu elektrického či magnetického pole, vstupní impedanci atd.).

Postup analýzy antény momentovou metodou byl již detailně popsán ve čl. 4.1, čl. 4.3 a čl. 4.4, a proto uvádíme jen stručnou rekapitulaci:

1. Analyzovanou strukturu rozdělíme na nábojové buňky a na buňky proudové. Tvar buněk volíme co nejjednodušší (obdélníkový). Dále předpokládáme, že náboj i proud budou na ploše jednotlivých buněk konstantní (ale na různých buňkách různé). Hlavní oblastí našeho zájmu přitom budou proudové buňky, neboť náboj lze na základě proudu stanovit z rovnice kontinuity. Síť proudových buněk je od sítě buněk nábojových posunuta o polovinu buňky.
2. Vyjádříme vztah mezi elektrickou intenzitou ve středu i-té proudové buňky a mezi proudy na všech buňkách (včetně i-té). Budeme požadovat, aby byly tečné složky elektrické intenzity ve středech všech buněk nulové vyjma buněk zdrojových (budeme předpokládat, že struktura bude buzena plovoucími ideálními napěťovými zdroji v horizontální rovině).
3. Jako výsledek dostáváme soustavu lineárních rovnic, jejímž řešením jsou hledané hodnoty proudů na všech buňkách.
4. Z nalezeného rozložení proudu na anténním prvku můžeme vypočíst hledanou vstupní impedanci. Vstupní impedanci však nelze vypočíst přímo, protože struktura je buzena napěťovým zdrojem umístěným v horizontálním směru, který se jedním pólem dotýká přívodního mikropásku a druhým pólem mikropásku pomocného (anglicky stub). Proto je třeba aplikovat celou řadu kroků, kterou označujeme jako de-embedding.

Podrobnější pohled na celou analýzu je relativně náročný, a proto jej celý uvádíme ve vrstvě B. Další informace může čtenář nalézt v knize [15]. Příklad výpočtu je popsán ve vrstvě C.

Závěrem ještě uveďme přehled komerčně vyráběných programů, založených na metodě momentů.

V některých ohledech jsou si výše uvedené programy podobné, v jiných se zásadně liší. Společnou vlastností uvedených programů je to, že používají tzv. plošnou formulaci metody momentů (tj. diskretizují se pouze elektricky či magneticky vodivé plošky), a to v kmitočtové oblasti. Zásadní rozdíl však spočívá v otevřenosti či uzavřenosti formulace. Formulace uzavřeného problému je jednodušší, neboť pro elektricky vodivou krabici vyplněnou vrstevnatým dielektrikem lze Greenovy funkce sestavit jednodušeji než pro otevřené vrstevnaté problémy.

Dalším společným rysem je to, že všechny tyto programy používají bázové funkce, které jsou několikrát menší než je délka vlny. Pro představu toho, jak rostou paměťové nároky [MB] na uchování matice koeficientů, slouží následující tabulka:

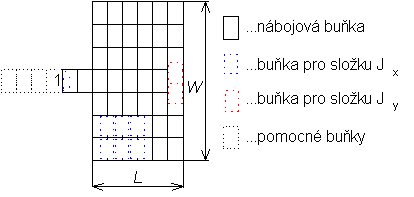
Podstatný rozdíl mezi programy spočívá v typu domény, ve které je problém formulován. Zatímco programy založené na prostorové verzi momentové metody mohou používat čtyřúhelníkové buňky (ty dobře kopírují reálné tvary kovových části struktury), u programů pracujících ve spektrální oblasti je přípustná pouze rovnoměrná síť elementárních pravoúhlých buněk. Čistě rovnoměrná síť vede k neúměrné velikosti výsledných matic, a proto je u programů Sonnet a Microwave Office aplikována technika podoblastí, které se vytvářejí sčítáním příspěvků elementárních buněk. Programy Sonnet a Microwave Office využívají dále algoritmus FFT k akceleraci dvojnásobných sumací, které ve spektrální momentové metodě nahrazují výpočet dvojného nevlastního integrálu. Rozdíl mezi programy Sonnet a Microwave Office je však v typu použité FFT: Microwave Office připouští, aby celkový počet buněk byl součinem prvočísel, Sonnet je díky standardní FFT omezen na mocniny dvou.

Programy Sonnet a Microwave Office mají oproti programům, pracujícím v prostorové doméně, tu výhodu, že pro bezeztrátové struktury jsou matice koeficientů v soustavě rovnic čistě reálné (při dané velikosti paměti můžeme dvakrát větší problémy, a navíc, stejně velký problém je díky reálné aritmetice řešen rychleji).

Závěrem je účelné provést krátké zhodnocení programů. Především lze říci, že všechny programy poskytují z hlediska vlnové analýzy běžnému uživateli přibližně totéž. Pochopitelně existují rozdíly v rychlosti a v jednoduchosti ovládání uživatelem. Pro celkové rychlostní srovnání by však bylo nutné vlastnit plné verze všech zmiňovaných programů. Lze však prohlásit, že programy založené na prostorové metodě momentů jsou rychlejší programy založené na spektrální verzi této metody. Cenou za větší rychlost programů založených na prostorové metodě momentů je větší náročnost při psaní softwaru.

Velmi důležitou stránkou věci je snadnost a promyšlenost ovládání. Z tohoto hlediska se např. Microwave Office těší velké oblibě.