4.5 Flíčková anténaPodrobnější popisV tomto odstavci se budeme věnovat momentové analýze dvojrozměrné mikropáskové antény. V podstatě se jedná o rozšíření postupu, popsaného v čl. 4.4, na další rozměr. Jak již bylo řečeno, potřebujeme vyjádřit intenzitu elektrického pole pomocí proudů a nábojů na buňkách. Učiníme tak prostřednictvím vektorového potenciálu A a potenciálu skalárního φ; oproti předchozím článkům uvažujeme pozitivní konvenci, tj. exp(+jkr)
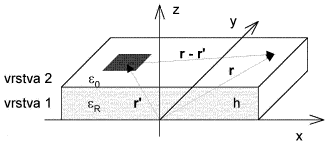
Vektorový potenciál A a skalární potenciál φ elementárních plošných proudů a nábojů přitom fyzikálně představují příspěvky těchto zdrojů k elektrickému poli v určitém bodě. Matematicky není snadné tyto potenciály získat, neboť jsou řešením tzv. Sommersfeldových integrálů. Pro některé jednoduché případy se však dají sestavit na základě fyzikálního pohledu na věc. Takový přístup uplatníme i zde. Uvažujme případ, kdy máme dvojrozměrný motiv anténního prvku nad zemní plochou (obr. 4.5B.1). Předpokládáme (pro tuto chvíli) relativní permitivitu dielektrika rovnu jedné a počítáme příspěvek elementární proudové a nábojové plošky v bodě r k intenzitě v bodě r'. Použijeme Coulombova (resp. Biot-Savartova) zákona s respektováním odrazu od zemní plochy (princip zrcadlení).
Tím dostaneme
kde pro vzdálenosti r0 a r1 platí
Zde r = (x, y), r' = (x'', y'') a h představuje tloušťku substrátu. Zahrnutí vlivu dielektrika už je obtížnější. Fyzikální představa říká, že vlna může do cílového bodu r přijít ne jednou, ale nekonečně mnoha cestami. V literatuře najdeme následující vztah:
kde a εr je relativní permitivita substrátu. Vektorový potenciál A zůstane i po přidání dielektrika nezměněn. V případě zdrojů konečné velikosti (tj. našich obdélníkových buněk) bude jejich příspěvek vyjádřen integrálně
Nyní je budeme věnovat diskretizaci rovnice (4.5B.2). Pro splnění tohoto úkolu musíme znát příspěvek libovolné proudové (resp. nábojové) buňky k potenciálu ve středu buňky jiné. Proto zavedeme označení
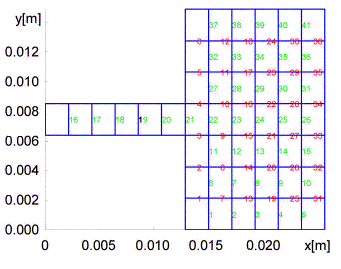
Výraz mijAx říká jak j-tá proudová buňka pro složku x přispívá k vektorovému potenciálu ve středu i-té buňky. Podobně je tomu i u výrazu mijAy pro složku Jy a u výrazu mijφ pro skalární potenciál. Jak jsme uvedli ve vrstvě A, jsou sítě proudových buněk a buněk nábojových navzájem posunuty o polovinu buňky, a používají tedy jiné číslování. Navíc proudové buňky mají nezávislé číslování pro složku Jx a pro složku Jy. Pro lepší představu číslování uvádíme na obr. 4.5B.2 síť nábojových buněk pro stejný případ, jako byl uveden na obr. 4.5A.3. Pro účely sestavení rovnic pro neznámé proudové hodnoty je nutné mít k dispozici funkci, která vypočte příspěvky mezi dvěma libovolnými buňkami (stejného typu). Díky rozsahu tohoto článku není možné detailně popsat, jak taková funkce pracuje.
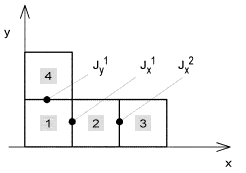
Důležité však je, že před prvním voláním funkce se vypočtou jen všechny nutné příspěvky, neboť příspěvky některých buněk se opakují (např. buňky 1 a 2 pro složku Jx mají stejný příspěvek jako buňky 3 a 4). Tyto všechny vzájemné příspěvky se uloží do tzv. momentové tabulky (matice). Při každém dalším volání funkce se pouze čte tento příspěvek na odpovídajícím místě momentové matice. Nyní se pokusíme o sestavení soustavy rovnic. Nebude zde však uveden obecný vztah pro obecný případ, ale bude ukázána konkrétní jednoduchá situace. V obr. 4.5B.3 je nakreslen motiv typu hokejka, který má čtyři nábojové buňky a tři buňky proudové (z toho dvě buňky pro Jx a jednu buňku pro Jy). Nyní sestavíme rovnice pro intenzitu E1x
První člen představuje příspěvek všech proudových buněk k proudové buňce Jx1. Druhý člen je příspěvkem od nábojových buněk; výraz {}/Δx představuje náhradu derivace ∂φ/∂x středovou diferencí (viz čl. 4.1). Obsahem složené závorky jsou čtyři členy, protože máme celkem čtyři nábojové buňky. Např. první člen představuje příspěvek první nábojové buňky do středu druhé buňky minus příspěvek první nábojové buňky do středu první buňky. Tj. první index u členů m je vždy střed cílové nábojové buňky, v níž příspěvek počítáme, a druhý index je pak index zdrojové nábojové buňky. Náboj sídlící v každé buňce je přitom spočten za pomoci proudových uzlových proudových hustot na stěnách s využitím rovnice kontinuity
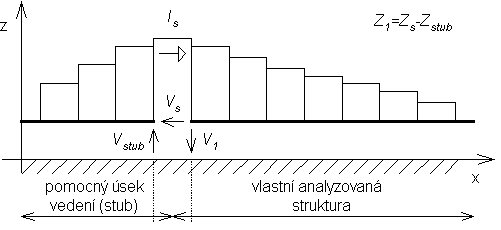
kde σ je v našem případě plošná hustota náboje. Podobným způsobem bychom sestavili rovnici pro intenzitu E2x a pro intenzitu E1y. Tolik tedy k sestavení rovnic. Dále se budeme věnovat buzení struktury. Nejjednodušším způsobem buzení struktury je buzení rovinnou vlnou (viz čl. 4.4). Stačí totiž pro každou proudovou buňku položit Ex = -ExI a Ey = -EyI, kde ExI a EyI představují složky intenzity dopadající vlny. My však budeme budit anténu horizontálním napěťovým zdrojem. Situaci pro případ struktury z obr. 4.5B.2 ukazuje obrázek 4.5B.4. V místě, kde byla v obr. 4.5B.2 symbolem 1 označena vstupní svorka, je nyní umístěn napěťový zdroj o napětí VS. Tento zdroj dodává do analyzované struktury proud IS. Jeden pól zdroje je připojen přímo na analyzovanou strukturu, druhý pak na pomocný mikropásek (tzv. stub), který představuje proti zemi určitou impedanci Zstub. Vstupní impedance Z1 je pak dána vztahem
kde impedanci ZS stanovíme z podílu napětí VS (jeho hodnotu si můžeme při analýze zvolit) a proudu IS. Impedanci Zstub stanovíme analyticky jako –Z0 cotg(β lstub).
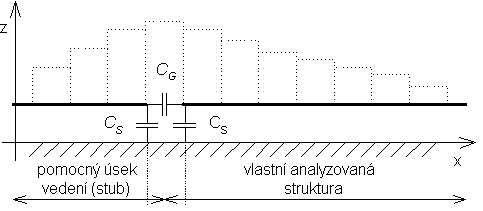
Pokud provedeme výpočet impedance naznačeným způsobem, nebude výsledek přesně odpovídat skutečnosti, protože jsme neuvážili vliv koncových kapacit (viz obr. 4.5B.5).
Při respektování kapacit je nutné k impedanci Zstub připočíst paralelně impedanci ZS = 1/jω CS (kapacita CS není kapacitou otevřeného konce, ale je menší). Tím získáme Zstub’ = Zstub || ZS. Kapacita CG je však už zahrnuta v impedanci ZS a po vypočtení impedance Z1‘ = ZS – Zstub‘ je nutné pouze odečíst ZS. Výsledná (korigovaná) impedance pak je Z1” = Z1‘ ZS / (Zs–Z1‘). Soustava rovnic pro neznámé uzlové hodnoty byla sestavena na základě fyzikálních úvah. Nyní uvedeme obecný matematický postup, odpovídající výše uvedeným úvahám:
Tím naše povídání o analýze mikropáskových antén momentovou metodou končí. Konkrétní příklady výpočtu uvádíme ve vrstvě C. |