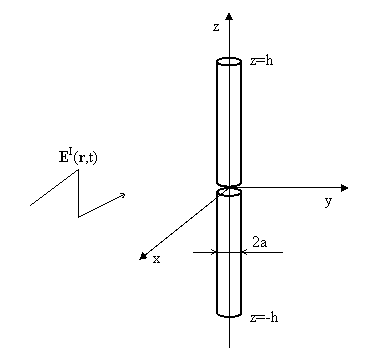
5.1 Modelování drátových antén v časové oblasti metodou momentů

Základní teorie

V kapitolách 4.1, 4.4 resp. 4.5 byly drátový dipól, mikropáskový dipól a flíčková anténa modelovány metodou momentů ve frekvenční oblasti. Integrální rovnice se převedla na soustavu algebraických rovnic a v ustáleném harmonické stavu se pro daný kmitočet vypočetlo rozložení proudu na anténě. Ze známého proudového rozložení je možné následně vypočítat další parametry antén.

Numerické modelování antén ve frekvenční oblasti je efektivní, pokud nás zajímají parametry antény jen v úzkém pásmu kmitočtů. V případě širokopásmové analýzy se místo analýzy v oblasti kmitočtové používá řešení v časové oblasti. Je nutné si ale uvědomit, že modelování v časové oblasti je vhodné jen pro analýzu struktur s nízkým činitelem jakosti, jinak je vypočtená odezvá příliš dlouhá a výpočetní algoritmus je časově náročný.

V této kapitole stručně popíšeme princip modelování drátových antén v časové oblasti. Stejně jako ve frekvenční oblasti řešíme formulace vycházející z Maxwellových rovnic diferenciálním, resp. v integrálním tvaru. V této kapitole zaměříme pozornost, podobně jako v kapitolách 4.1, 4.4 a. 4.5, na integrální tvar.

Integrální formulace rovnic v časové oblasti je komplikovanější než ve frekvenční oblasti pro ustálený harmonický stav, protože v časové formulaci se vyskytuje derivace vektorového potenciálu dle času, takže namísto rovnice integrální řešíme vlastně rovnici integro-diferenciální. 

Z metodických důvodu se zde zaměříme jen na řešení symetrického drátového dipólu, protože řešení složitějších struktur je z hlediska odvození a implementace komplikovanější.

Modelování drátového dipólu v časové oblasti metodou momentů

Při analýze symetrického drátového dipólu v časové oblasti budeme vycházet z obdobné situace, jako tomu bylo v oblasti kmitočtové. Předpokládejme, že symetrický drátový dipól je vyroben z dokonalého elektrického vodiče a je umístěn ve vakuu. Osa dipólu je totožná se směrem osy z válcového souřadného systému a na dipól kolmo dopadá rovinná elektromagnetická vlna (obr. 5.1A.1). Intenzita elektrického pole dopadající vlny je přitom rovnoběžná s osou dipólu a má obecný časový průběh. Dále budeme předpokládat, že poloměr dipólu a je podstatně menší než vlnová délka.

Obr. 5.1A.1 Dipól umístěný podél osy z buzený elektromagnetickou vlnou.

Dopadající rovinná elektromagnetická vlna s obecným časovým průběhem E^I indukuje proud I_z (dipól je umístěn v ose z) na povrchu dokonale vodivé antény. Jelikož na otevřených koncích antény nemají elektrické proudy kam téci, hromadí se zde náboj, popsaný nábojovou hustotou σ. V následujících časových okamžicích akumulovaný náboj postupně odtéká a znovu přitéká v závislosti na fázi jednotlivých spektrálních složek budicí vlny. Indukované proudy a náboje se stávají zdroji vyzařované sekundární vlny. Působení proudu tekoucího ve směru z, může být popsáno pomocí vektorového potenciálu [37]

Působení nábojové hustoty může být popsáno pomocí potenciálu skalárního

Hodnotu vektorového potenciálu A_z v libovolném „cílovém“ bodě z, v čase t vypočteme postupným sčítáním příspěvků složek proudů ze všech „zdrojových“ bodů ξ na ose anténního vodiče. Zdrojový proud přitom musíme zpozdit o čas R/c, který vlna potřebuje ke zdolání vzdálenosti mezi zdrojovým bodem ξ a bodem cílovým z; tedy

Dále, c v (5.1A.1) značí rychlost světla v daném prostředí. Velikost příspěvku k vektorovému potenciálu je dále nepřímo úměrná vzdálenosti mezi zdrojovým a cílovým bodem. Integraci provádíme podél celé antény. Hodnotu integrálu násobíme permeabilitou prostředí μ , jež obklopuje anténu (vakuum).

Co se týká vztahu pro výpočet skalárního potenciálu, rozložení proudu je nahrazeno délkovou hustotou náboje σ. Výsledek integrace je namísto násobení permeabilitou dělen permitivitou ε okolního prostoru. Vše ostatní ve vztahu (5.1A.2) zůstává beze změny vůči (5.1A.1).

Vzhledem k tomu, že proud a náboj jsou na anténně vzájemně svázány, musíme vztahy (5.1A.1) a (5.1A.2) doplnit rovnicí kontinuity, která tuto vazbu matematicky popisuje

Známe-li vektorový a skalární potenciál, můžeme vypočítat intenzitu elektrického pole vlny vyzařované anténou E_z^S

Časová derivace vektorového potenciálu popisuje „dynamický příspěvek“ elektrických nábojů na anténě k vyzařované vlně (zdrojem vektorového potenciálu jsou totiž elektrické vodivé proudy, náboje v pohybu). Parciální derivace skalárního potenciálu podle proměnné z vyjadřuje „statický příspěvek“ elektrických nábojů na anténě k vyzařované vlně (zdrojem skalárního potenciálu jsou nyní statické náboje, koncentrované na koncích antény).

Na povrchu dokonale elektricky vodivého anténního vodiče musí elektrická intenzita splňovat okrajovou podmínku

Soustava rovnic (5.1A.1) až (5.1A.6) se řeší numericky v podstatě ve dvou krocích. První spočívá v prostorové diskretizaci problému a druhý v aplikaci časových algoritmů na výsledek prvního kroku řešení.

První krok je analogický řešení ve frekvenční oblasti, kde byla metoda momentů použita pro převod integrální rovnice na soustavu algebraických rovnic. Zde opět použijeme metodu momentů, a to pro převod integro-diferenciální rovnice (5.1A.5) na soustavu zpožděných diferenciálních rovnic (prostorová diskretizace problému).

Pro vykonání druhého kroku (aplikace časových algoritmů) je možné použít buď explicitní, nebo implicitní algoritmus. U explicitního přístupu platí pro délku časového kroku Δt podmínka Δt ≤ R_min/c, kde R_min je nejmenší vzdálenost středů diskretizačních elementů a c je rychlost světla v daném prostředí. V případě implicitního přístupu délka kroku může být libovolná. Větší délka časového kroku zvětšuje rychlost výpočtu, ale klesá jeho přesnost. Tyto přístupy bývají často označovány jako MOT (marching on in time).

Další metoda je založena na aproximaci časové odezvy Laguerrovými polynomy a bývá označována jako MOO (marching on in order). Výhodou MOO je nepodmíněná stabilita, nevýhodou vyšší náročnost na implementaci a menší efektivnost ve srovnání s MOT.

Vzhledem k výše uvedeným skutečnostem se zaměříme na MOT. I když jsme zmínili, že soustava (5.1A.1) až (5.1A.6) se řeší ve dvou krocích (prostorová diskretizace a aplikace časových algoritmů), oba kroky sloučíme dohromady. Je dobré si uvědomit, že pomocí MOT převedeme soustavu zpožděných diferenciálních rovnic na soustavu rovnic diferenčních (v principu jde o nahrazení derivací podle času vektorového potenciálu v (5.1A.5) vhodnou diferencí).

Výhodou explicitního přístupu je jednodušší implementace a také zde není potřeba počítat inverzní matici jako v případě řešení ve frekvenční oblasti, popř. jako u implicitního přístupu. Avšak explicitní přístup často trpí nestabilitou řešení (vypočtená odezva se neustálí po odeznění budícího impulsu, ale roste nade všechny meze, tzv. late time oscillation). Proto v této kapitole bude zaměřena pozornost jen na implicitní přístup.

Budicí impuls

Dříve, než zaměříme pozornost na implicitní přístup, vyberme vhodný časový průběh budicího impulsu.

Pokud bychom pro buzení zvolili Diracův impuls, bylo by spektrum budicího signálu rovnoměrně rozprostřeno přes celou nekonečnou kmitočtovou oblast. Jelikož v technické praxi vyžadujeme řešení pouze pro omezené pásmo kmitočtů a jelikož ani nemáme k dispozici neomezený paměťový prostor a neomezený výpočetní výkon počítače, nejeví se Diracův impuls jako ideální volba.

Namísto Diracova impulsu je vhodnější použít impulsu Gaussova modulovaného harmonickým signálem. Změnou parametrů tohoto impulsu lze analyzovat jen to pásmo kmitočtů, které nás zajímá.

Vektor intenzity elektrického pole Gaussova budicího impulsu modulovaná harmonickým signálem je dán vztahem

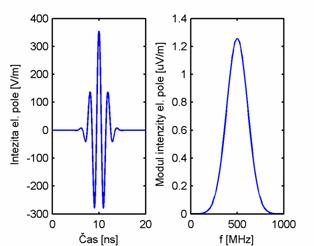
kde E₀ značí vektor intenzity elektrického pole budicí vlny v počátku souřadného systému, r je polohový vektor bodu, v němž intenzitu budicí vlny počítáme, a_k značí jednotkový vektor ve směru šíření vlny, c je rychlost světla v daném prostředí, T značí šířku Gaussova impulsu (čas, během něhož je amplituda Gaussova impulsu větší než 2% vrcholové hodnoty), t je aktuální časový okamžik, t₀ značí vzdálenost vrcholu Gaussova impulsu od počátku časové osy a f₀ je střední kmitočet analyzovaného pásma. Příklad Gaussova impulsu modulovaného harmonickým signálem spolu s jeho spektrem, definovaný následujícími parametry: |E₀|=120π V/m, T=8 ns, t₀=10 ns a f₀= 500 MHz je zobrazen na obr. 5.1A.2.

Obr. 5.1A.2 Časový průběh (vlevo) Gaussuva impulsu modulovaného harmonickým signálem a jeho spektrum (vpravo).

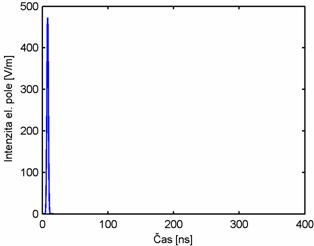
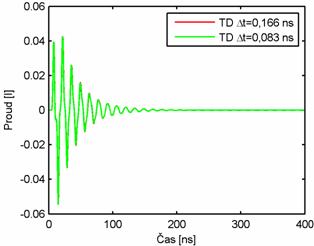
Implicitní algoritmus

Odvození implicitního algoritmu je náročné (soustava rovnic (5.1A.1) až (5.1A.6) je diskretizována v prostoru a čase) a pro zainteresovaného čtenáře je uvedeno ve vrstvě B. V této vrstvě budou diskutovány jen jeho vlastnosti.

U implicitního algoritmu, na rozdíl od explicitního, musíme řešit inverzní matici a jeho implementace na počítači je náročnější než v případě explicitního algoritmu. Avšak jeho nespornou výhodou je, že délka časového kroku může být volena libovolně (je nutné mít ale na paměti, že délka časového kroku ovlivňuje přesnost výpočtu viz dále), a hlavně tento algoritmus je podstatně stabilnější než explicitní.

Použití implicitního algoritmu bude demonstrováno na analýze drátového dipólu délky 2 m a poloměru 2 mm, který je ve svém středu buzen Gaussovým impulsem modulovaný harmonickým signálem dle (5.1A.7) definovaným následujícími parametry: E₀=120π V/m, T = 6 ns, t₀ = 8 ns, f₀ = 0 Hz. Vzhledem k tomu, že střední kmitočet analyzovaného pásma je 0 Hz, dále budeme nazývat tento budící impuls, jen jako Gaussův impuls. Délku časové analýzy zvolíme 400 ns. Tělo dipólu je rozděleno na 40 segmentů (prostorová disretizace úlohy). Analýzu drátového dipólu provedeme dvakrát pro dvě různé délky časového kroku. Při první analýze volíme délku časového kroku Δt = R_min/c = 0.166 ns, cΔt = 0,05 m a ve pří druhé analýze volíme délku časového kroku poloviční, tj. Δt = R_min/(2c) = 0.083 ns, cΔt = 0,025 m (časová diskretizace úlohy).

Budicí Gaussův impuls je zobrazen na obr. 5.1A.3. Vypočtené odezvy proudu na tento impuls ve středu dipólu jsou zobrazeny na obr. 5.1A.4. Z porovnání obou obrázků je vidět, že odezvy proudu jsou podstatně delší než budicí impuls a rozdíl mezi vypočtenými odezvami proudu je nepatrný.

Drátový dipól je ve své podstatě úzkopásmová anténa, která je schopna „transformovat“ energii do volného prostoru jen v omezeném pásmu kmitočtů. Vzhledem k tomu, že budicí impuls nese energii na kmitočtech, kde anténa tuto schopnost má podstatně menší, dochází k přelévání energie z jednoho ramene na druhé a zpět a k postupnému vyzařování.

Obr. 5.1A.3 Budicí Gaussův impuls.

Obr. 5.1A.4 Odezvy proudu na Gaussův impuls (obr. 5.1A.3) ve středu drátové antény pro různé délka časového kroku implicitního algoritmu.

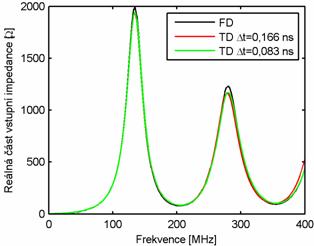
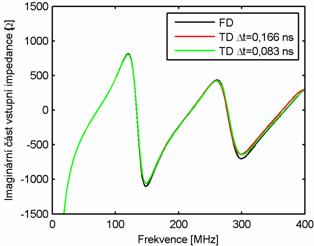
Vzhledem k tomu, že vypočtené odezvy proudu jsou ustálené, můžeme vypočítat vstupní impedanci analyzované drátové antény (obr. 5.1A.5, označeny TD). Ve stejném obrázku je vstupní impedance vypočtena pro porovnání metodou momentů ve frekvenční oblasti (označeno FD). Řešení ve frekvenční oblasti bereme jako referenční. Porovnáme-li toto řešení s výsledky pro implicitní algoritmus pro délku časového kroku Δt = R_min/c = 0.166 ns, cΔt = 0,05 m (červená křivka), tak z obrázku je vidět, že větší rozdíly se objevují v oblasti vyšších kmitočtů. Tyto rozdíly jsou hlavně způsobeny diskretizací řešených rovnic (5.1A.1) až (5.1A.6) v čase. Pokud ale u implicitního algoritmu zmenšíme délku časového kroku na polovinu (zelená křivka), tak jsou rozdíly i na vyšších kmitočtech minimální (přesnější aproximace problému v čase). Délka časového kroku má vliv na přesnost algoritmu.

Obr. 5.1A.5 Reálná (vlevo) a imaginární (vpravo) část vstupní impedance analyzovaného drátového dipólu.

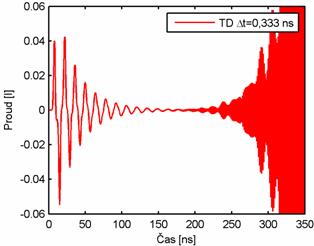
Délka časového kroku ovlivňuje nejen přesnost, ale i stabilitu algoritmu. Tato skutečnost je demonstrována na obr. 5.1A.6, kde je zobrazena proudová odezva, která byla získána analýzou drátového dipólu za stejných podmínek, jen délka časového kroku je dvojnásobná, tj. Δt = 2R_min/c = 0.333 ns, cΔt = 0,1 m. Vypočtená odezva není ustálená, ale roste nade všechny meze.

Obr. 5.1A.6 Nestabilní odezva proudu na Gaussův impuls z obr. 5.1A.3 ve středu drátového dipólu (větší délka časového kroku).

Pro stabilizaci časového algoritmu se používají různé techniky, avšak ty jsou již nad rámec této kapitoly.