Multimedia textbook

5.1 Time-domain modeling of wire antennas by method of moments

Advanced theory

In this layer the implicit algorithm will be derived by solving the system of the equations (5.1A.1) to (5.1A.6) for the wire dipole which is placed along the z axis (fig. 5.1B.1). Since only z components of the vector potential and the intensity of electric field are in this system of equations, it is not necessary to distinguish among the components of vectors. Thus, in the following text, the subscript z will be omitted.

The implicit algorithm will be derived from the equation (5.1A.5) which can be rewritten by considering the boundary condition (5.1A.6) to the following form

\frac{\partial A (z, t)}{\partial t} + \frac{\partial φ (z, t)}{\partial z} = E_{}^{I} (z, t)

( 5.1B.1 )

Now, let’s carry out the first step of the solution, the application of the method of moments to (5.1B.1). Let’s divide the wire dipole to N segments of the same length Δz and denote the ends of the segments by coordinates z₀, z₁, …, z_N+1 (fig. 5.1B.1). Further, let’s denote the center of segments by z₀⁺, z₁⁺, …, z_N⁺, and z₁^-, z₂^-, …, z_N+1^-, respectively. For the expansion of the current distribution on the wire dipole in space, let’s use the constant basis functions: in the region of a current cell (fig. 5.1B.1), which is bounded by the coordinates either z_n⁺, z_n+1⁺ or z_n-1^-, z_n^-, the constant current distribution is supposed. It is appropriate to remember, that the current at the end of the wire is equal to zero, because it can not flow anywhere. In the region of a charge cell, which is bounded by the coordinates z_n, z_n+1, the constant charge density distribution is supposed.

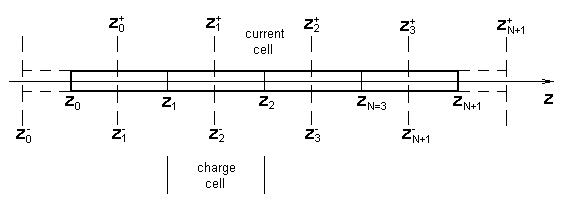Fig. 5.1B.1

Wire dipole discretization.

The constant basis functions are in the region of the current cell defined by the following relation

f_{n} = {\begin{cases} 1 z_{n} - \frac{Δ z}{2} \leq z \leq z_{n} + \frac{Δ z}{2} \\ 0 o t h e r w i s e \end{cases}

( 5.1B.2 )

By these basis functions and time dependant unknown current coefficients I_n(t) the time-space current distribution in (5.1A.1) can be approximated

I (z, t) \approx \sum_{n = 1}^{N} I_{n} (t) f_{n} (z)

( 5.1B.3 )

Let’s discretize our wire dipole in time (the second step). Let’s divide the time step to the equal intervals of the length Δt and denote the individual time instant on time axes by t_k=kΔt for k = 0, 1, 2, …, ∞. At these time instants the current distribution on the wire antenna is be computed.

Substituting (5.1B.3) to (5.1A.1) and (considering (5.1B.2)) the vector potential at the point z_m and the time instant t_k can be written in the following form

A (z_{m}, t_{k}) = \frac{μ}{4 π} \int_{ξ = - h}^{h} \frac{I (ξ, t_{n} - R (z_{m}, ξ) / c)}{\sqrt{a^{2} + {| z_{m} - ξ |}^{2}}} d ξ \approx \frac{μ_{0}}{4 π} \int_{ξ = - h}^{h} \frac{\sum_{n = 1}^{N} I_{n} (t_{n} - R (z_{m}, ξ) / c) f_{n} (ξ)}{\sqrt{a^{2} + {| z_{m} - ξ |}^{2}}} d ξ = \sum_{n = 1}^{N} I_{n} (t_{R k} (m, n)) κ (m, n)

( 5.1B.4 )

where

κ (m, n) = \frac{μ}{4 π} \int_{ξ = z_{n} - \frac{Δ z}{2}}^{z_{n} - \frac{Δ z}{2}} \frac{d ξ}{\sqrt{a^{2} + {| z_{m} - ξ |}^{2}}} = \frac{μ}{4 π} {\ln [z_{m} - z_{n} + \frac{Δ z}{2} + \sqrt{{(z_{m} - z_{n} + \frac{Δ z}{2})}^{2} + a^{2}}] - \ln [z_{m} - z_{n} - \frac{Δ z}{2} + \sqrt{{(z_{m} - z_{n} - \frac{Δ z}{2})}^{2} + a^{2}}]}

( 5.1B.5 )

t_{R k} (m, n) = t_{k} - R (m, n) / c

( 5.1B.6 )

R (m, n) = \sqrt{a^{2} + {| z_{m} - z_{n} |}^{2}}

( 5.1B.7a )

R (m, n) = | z_{m} - z_{n} |

( 5.1B.7b )

For the evaluation of the distance $R (m, n)$ in (5.1B.6) the accurate relation (5.1B.7a), or the approximate one (5.1B.7b), which neglects the radius of a wire a, can be used. Using the approximate relation increases the stability of the algorithm, however, it is possible to use it only if the length of the time step multiplied by the speed of light in the surrounding medium is much larger, than the radius of the wire (cΔt>>a). Otherwise, the accuracy falls down. Using the approximate relation was introduced in [37] and if the mentioned condition is met, it is appropriate to use (5.1B.7b). The interested reader can test the influence of that neglect on the accuracy and stability of the algorithm.

Let’s discretize the scalar potential (5.1A.2) where the space-time charge density distribution is the unknown quantity. The charge density can be computed with the continuity equation (5.1A.4) which can be rewritten in the following form

σ (z, t) = - \int \frac{\partial I (z, t)}{\partial z} d t

( 5.1B.8 )

Substituting the space-time charge density distribution (5.1B.3) to (5.1B.8) and approxiomating the partial differentiation of the current with respect to variable z by the center difference, the continuity equation (5.1B.8), after the swap of the derivation and integration, can be written

σ (z, t) \approx - \frac{\partial \sum_{n = 1}^{N} \int I_{n} (t) d t f_{n} (z)}{\partial z} \approx - \sum_{n = 0}^{N} \frac{\int I_{n + 1} (t) d t - \int I_{n} (t) d t}{Δ z} f_{n}^{+} (z)

( 5.1B.9 )

Since the constant basis functions are used for the space approximation of the current (5.1B.3), the partial derivative with respect to variable z in (5.1B.9) could not be computed straightforwardly (the derivative of the constant function is equal to zero), but the center difference has to be used. To be the differentiating correct, the integral of currents with respect to time at the ends of the wire were included in (5.1B.9), although they are equal to zero. In the last step in (5.1B.9) the basis functions were swaped: from the spacious approximation of the current by the basis functions f_n(z) we got toward the approximation of the charge density by the basis functions f_n⁺(z).

Substituting the continuity equation (5.1B.9) to (5.1A.2) the scalar potential at the point z_m⁺ and the instant t_k can be evaluated

\begin{array}{l} φ (z_{m}^{+}, t_{k}) = - \frac{1}{4 π ε} \int_{ξ = - h}^{h} \frac{σ (ξ, t_{k} - R (z_{m}^{+}, ξ) / c)}{R (z_{m}^{+}, ξ)} d ξ \approx - \frac{1}{4 π ε} \int_{ξ = - h}^{h} \sum_{n = 0}^{N} \frac{\int_{0}^{t_{k} - R (z_{m}^{+}, ξ) / c} I_{n + 1} (t) d t - \int_{0}^{t_{k} - R (z_{m}^{+}, ξ) / c} I_{n} (t) d t}{Δ z} f_{n}^{+} (ξ) \frac{1}{R (z_{m}^{+}, ξ)} d ξ = \\ = \sum_{n = 1}^{N} \frac{\int_{0}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t κ (m^{+}, n^{+})}{Δ z} - \sum_{n = 1}^{N} \frac{\int_{0}^{t_{R k} (m^{+}, n^{-})} I_{n} (t) d t κ (m^{+}, n^{-})}{Δ z} = φ (z_{m}^{+ +}, t_{k}) - φ (z_{m}^{+ -}, t_{k}) \end{array}

( 5.1B.10 )

where

t_{R k} (m^{\pm}, n^{\pm}) = t_{k} - R (m^{\pm}, n^{\pm}) / c

( 5.1B.11 )

R (m^{\pm}, n^{\pm}) = \sqrt{a^{2} + {| z_{m}^{\pm} - z_{n}^{\pm} |}^{2}}

( 5.1B.12a )

R (m^{\pm}, n^{\pm}) = | z_{m}^{\pm} - z_{n}^{\pm} |

( 5.1B.12b )

κ (m^{\pm}, n^{\pm}) = \frac{1}{4 π ε} \int_{ξ = z_{n}^{\pm} - \frac{Δ z}{2}}^{z_{n}^{\pm} - \frac{Δ z}{2}} \frac{d ξ}{\sqrt{a^{2} + {| z_{m}^{\pm} - ξ |}^{2}}} = \frac{1}{4 π ε} {\ln [z_{m}^{\pm} - z_{n}^{\pm} + \frac{Δ z}{2} + \sqrt{{(z_{m}^{\pm} - z_{n}^{\pm} + \frac{Δ z}{2})}^{2} + a^{2}}] - \ln [z_{m}^{\pm} - z_{n}^{\pm} - \frac{Δ z}{2} + \sqrt{{(z_{m}^{\pm} - z_{n}^{\pm} - \frac{Δ z}{2})}^{2} + a^{2}}]}

( 5.1B.13 )

Here, as in case of the evaluating of the vector potential, it is possible to use for the evaluation of the distance $R (m^{\pm}, n^{\pm})$ in (5.1B.11) either the accurate relation (5.1B.12a), or the approximate relation (5.1B.12b). The reasons and the condition are the same as in case of the evaluation of the vector potential.

Similarly the scalar potential at the point z_m and the time instant t_k can be evaluated z_m^-

φ (z_{m}^{-}, t_{k}) = φ (z_{m}^{- +}, t_{k}) - φ (z_{m}^{- -}, t_{k})

( 5.1B.14 )

To evaluate the relations (5.1B.10) and (5.1B.14), it is necessary to compute the integral of the current with respect to time. The integral can be evaluated according to different numerical integration rules. We choose the trapezoid rule because its implementation is easy and offers sufficient accuracy. By this rule, the integral of the current in the interval from 0 to t_k,, in case of the equidistant division of the interval, can be computed

\int_{0}^{t_{k}} I (t) d t \approx Δ t [\frac{I (t_{0} = 0)}{2} + \sum_{l = 1}^{k - 1} I (t_{l}) + \frac{I (t_{k})}{2}]

( 5.1B.15 )

Now, let’s go back to (5.1B.1) and discretize it. Let’s approximate the first derivative of the vector potential with respect to time by the center difference of the first order. By this step the partial derivative of the vector potential is evaluated at the point z_mand the time instant t_k-1/2. To be the calculation sufficiently accurate, the partial derivative of the scalar potential with respect to variable z has to be evaluated at the same point and the time instant. This can be reached by using the center differentiation for the scalar potential at the points z_m⁺ and z_m^- at two instants t_k and t_k-1. The average of these central differences is actually numerically evaluated the derivative of the scalar potential at the point z_mand the time instant t_k-1/2. Of course, the excitation pulse has to be evaluated at the same point and the instant as the vector and scalar potentials. After this steps the equation (5.1B.1) can be rewritten into the following form

\frac{A (z_{m}, t_{k}) - A (z_{m}, t_{k - 1})}{Δ t} + \frac{1}{2 Δ z} (φ (z_{m}^{+}, t_{k}) - φ (z_{m}^{-}, t_{k}) + φ (z_{m}^{+}, t_{k - 1}) - φ (z_{m}^{-}, t_{k - 1})) = E_{}^{I} (z, t_{k - 1 / 2})

( 5.1B.16 )

Rearranging terms in (5.1B.16) we obtain

\begin{array}{l} A (z_{m}, t_{k}) + \frac{Δ t}{2 Δ z} (φ (z_{m}^{+}, t_{k}) - φ (z_{m}^{-}, t_{k})) = Δ t E_{}^{I} (z, t_{k - 1 / 2}) + A (z_{m}, t_{k - 1}) \\ - \frac{Δ t}{2 Δ z} (φ (z_{m}^{+}, t_{k - 1}) - φ (z_{m}^{-}, t_{k - 1})) \end{array}

( 5.1B.17 )

The vector potential on the left-side of the equation (5.1B.17), computed according to (5.1B.4), can be transcribed

A (z_{m}, t_{k}) = A_{1} (z_{m}, t_{k}) + A_{2} (z_{m}, t_{k})

( 5.1B.18 )

where

A_{1} (z_{m}, t_{k}) = \sum_{n = 1}^{N} I_{n} (t_{R k} (m, n)) κ (m, n) f o r t_{R k} (m, n) > t_{k - 1}

( 5.1B.19a )

A_{2} (z_{m}, t_{k}) = \sum_{n = 1}^{N} I_{n} (t_{R k} (m, n)) κ (m, n) f o r t_{R k} (m, n) \leq t_{k - 1}

( 5.1B.19b )

For evaluating A₁(z_m, t_k), only the contributions of currents at delayed time instants t_Rk(m, n)>t_k-1 are considered (the unknowns currents). In case of the evaluating of A₂(z_m, t_k), only the contributions of currents at delayed instants t_Rk(m, n)≤t_k-1 are considered (the known currents). The unknown current at the time instant t_Rk(m, n) in the interval from t_k-1 to t_k can be evaluated

I (t_{R k} (m, n)) = \frac{R (z_{m}, z_{n})}{c} I (t_{k - 1}) + (1 - \frac{R (z_{m}, z_{n})}{c}) I (t_{k})

( 5.1B.20 )

Substituting (5.1B.20) to (5.1B.19a), A₁(z_m, t_k) can be expressed by the unknown and known currents at the instants t_kand t_k-1

A_{1} (z_{m}, t_{k}) = A_{11} (z_{m}, t_{k}) + A_{12} (z_{m}, t_{k})

( 5.1B.21 )

where

A_{11} (z_{m}, t_{k}) = \sum_{n = 1}^{N} (1 - \frac{R (z_{m}, z_{n})}{c Δ t}) κ (m, n) I_{n} (t_{k}) = \sum_{n = 1}^{N} A_{11 C} (m, n) I_{n} (t_{k})

( 5.1B.22a )

A_{12} (z_{m}, t_{k}) = \sum_{n = 1}^{N} \frac{R (z_{m}, z_{n})}{c Δ t} κ (m, n) I_{n} (t_{k}) = \sum_{n = 1}^{N} A_{12 C} (m, n) I_{n} (t_{k})

( 5.1B.22b )

The term A₁₁(z_m, t_k) contains only the unknown currents at the instant t_k.

Now, let’s focus our attention on the rest of the right-side of the equation (5.1B.17). The scalar potential (5.1B.10) at the point z_m⁺ can be evaluated

φ (z_{m}^{+}, t_{k}) = φ (z_{m}^{+ +}, t_{k}) - φ (z_{m}^{+ -}, t_{k})

( 5.1B.23 )

where the terms on the right-side (5.1B.23) can be expressed as the vector potential (5.1B.18). Let’s focus our attention on the first term

φ (z_{m}^{+ +}, t_{k}) = φ_{1} (z_{m}^{+ +}, t_{k}) + φ_{2} (z_{m}^{+ +}, t_{k})

( 5.1B.24 )

where

\begin{array}{l} φ_{1} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \int_{0}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t \frac{κ (m^{+}, n^{+})}{Δ z} f o r t_{R k} (m^{+}, n^{+}) > t_{k - 1} \end{array}

( 5.1B.25a )

\begin{array}{l} φ_{2} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \int_{0}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t \frac{κ (m^{+}, n^{+})}{Δ z} f o r t_{R k} (m^{+}, n^{+}) \leq t_{k - 1} \end{array}

( 5.1B.25b )

The situation is analogical as for the vector potential, however more complicated, because of the integral of the current with respect to time in (5.1B.25). Since the term φ₁(z_m⁺⁺, t_k) contains the unknown current at the time instant t_k, let’s express the integral of the current over the interval from 0 to t_Rk(m+, n+) in (5.1B.25a) as the sum of two integrals

\begin{array}{l} φ_{1} (z_{m}^{+ +}, t_{k}) = φ_{1}' (z_{m}^{+ +}, t_{k}) + φ_{13} (z_{m}^{+ +}, t_{k}) \end{array}

( 5.1B.26 )

where

\begin{array}{l} φ_{1}' (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \int_{t_{k - 1}}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t \frac{κ (m^{+}, n^{+})}{Δ z} \end{array}

( 5.1B.27a )

\begin{array}{l} φ_{13} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{κ (m^{+}, n^{+})}{Δ z} \int_{0}^{t_{k - 1}} I_{n} (t) d t = \sum_{n = 1}^{N} φ_{13 C} (m^{+}, n^{+}) \int_{0}^{t_{k - 1}} I_{n} (t) d t \end{array}

( 5.1B.27b )

The term φ₁₃(z_m⁺⁺, t_k) in (5.1B.27b) can be easily evaluated, since it contains only the known values of the currents. However, the term φ₁’(z_m⁺⁺, t_k) contains the unknown current at the time instant t_k. Therefore we express φ₁’(z_m⁺⁺, t_k) by the trapezoid rule for the numerical evaluation of the integral in the interval from t_k-1 to t_Rk(m+, n+), and the relations (5.1B.18) and (5.1B.20)

\begin{array}{l} φ_{1}' (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{Δ t}{2} (\frac{t_{R k} (m^{+}, n^{+}) - t_{k - 1}}{Δ t}) (I_{n} (t_{R k} (m^{+}, n^{+})) + I_{n} (t_{k - 1})) \frac{κ (m^{+}, n^{+})}{Δ z} = \\ = \sum_{n = 1}^{N} \frac{Δ t}{2} (1 - \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t}) [I_{n} (t_{k - 1}) \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t} + \\ + (1 - \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t}) I_{n} (t_{k}) + I_{n} (t_{k - 1})] \frac{κ (m^{+}, n^{+})}{Δ z} = \\ = φ_{11} (z_{m}^{+ +}, t_{k}) + φ_{12} (z_{m}^{+ +}, t_{k}) \end{array}

( 5.1B.28 )

where

\begin{array}{l} φ_{11} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{Δ t}{2 Δ z} {(1 - \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t})}^{2} κ (m^{+}, n^{+}) I_{n} (t_{k}) = \sum_{n = 1}^{N} φ_{11 C} (m^{+}, n^{+}) I_{n} (t_{k}) \end{array}

( 5.1B.29a )

\begin{array}{l} φ_{12} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{Δ t}{2 Δ z} (1 - \frac{R^{2} (z_{m}^{+}, z_{m}^{+})}{c^{2} Δ t^{2}}) κ (m^{+}, n^{+}) I_{n} (t_{k - 1}) = \sum_{n = 1}^{N} φ_{12 C} (m^{+}, n^{+}) I_{n} (t_{k - 1}) \end{array}

( 5.1B.29b )

Now only the term φ₁₁(z_m⁺⁺, t_k) contains the unknown current at the time instant t_k. This one can be easily expressed by (5.1B.29a). The relation (5.1B.24) can be expressed, considering (5.1B.25) to (5.1B.29), as follow

φ (z_{m}^{+ +}, t_{k}) = φ_{11} (z_{m}^{+ +}, t_{k}) + φ_{12} (z_{m}^{+ +}, t_{k}) + φ_{13} (z_{m}^{+ +}, t_{k}) + φ_{2} (z_{m}^{+ +}, t_{k})

( 5.1B.30 )

Analogically we can proceed with the evaluation of the term φ (z_m^+-, t_k)

φ (z_{m}^{+ -}, t_{k}) = φ_{11} (z_{m}^{+ -}, t_{k}) + φ_{12} (z_{m}^{+ -}, t_{k}) + φ_{13} (z_{m}^{+ -}, t_{k}) + φ_{2} (z_{m}^{+ -}, t_{k})

( 5.1B.31 )

or the scalar potential at the point z_m^-and the time instant t_k φ(z_m^-, t_k).

φ (z_{m}^{-}, t_{k}) = φ (z_{m}^{- +}, t_{k}) - φ (z_{m}^{- -}, t_{k})

( 5.1B.14 )

where

φ (z_{m}^{- +}, t_{k}) = φ_{11} (z_{m}^{- +}, t_{k}) + φ_{12} (z_{m}^{- +}, t_{k}) + φ_{13} (z_{m}^{- +}, t_{k}) + φ_{2} (z_{m}^{- +}, t_{k})

( 5.1B.32a )

φ (z_{m}^{- -}, t_{k}) = φ_{11} (z_{m}^{- -}, t_{k}) + φ_{12} (z_{m}^{- -}, t_{k}) + φ_{13} (z_{m}^{- -}, t_{k}) + φ_{2} (z_{m}^{- -}, t_{k})

( 5.1B.32b )

The terms on the right-sides of the relations (5.1B.31) and (5.1B.32) can be expressed similarly as the terms on the right-sides of relations (5.1B.24) to (5.1B.29) by changing the corresponding superscripts + and -, or vice versa.

Substituting (5.1B.10), (5.1B.14), (5.1B.18) to (5.1B.21) and (5.1B.24) to (5.1B.32) into the left-side of the relation (5.1B.17) and by rearranging the terms in this equation we obtain

\begin{array}{l} A_{11} (z_{m}, t_{k}) + \frac{Δ t}{2 Δ z} φ_{11} (z_{m}^{}, t_{k}) = Δ t E_{}^{I} (z_{m}, t_{k - 1 / 2}) - A_{12} (z_{m}, t_{k}) - A_{2} (z_{m}, t_{k}) + A (z_{m}, t_{k - 1}) - \\ - \frac{Δ t}{2 Δ z} (φ_{12} (z_{m}^{}, t_{k}) + φ_{13} (z_{m}^{}, t_{k}) + φ_{2} (z_{m}^{}, t_{k}) + φ (z_{m}^{+}, t_{k - 1}) - φ (z_{m}^{-}, t_{k - 1})) \end{array}

( 5.1B.33 )

where

φ_{11} (z_{m}^{}, t_{k}) = φ_{11} (z_{m}^{+ +}, t_{k}) - φ_{11} (z_{m}^{+ -}, t_{k}) - φ_{11} (z_{m}^{- +}, t_{k}) + φ_{11} (z_{m}^{- -}, t_{k})

( 5.1B.34a )

φ_{12} (z_{m}^{}, t_{k}) = φ_{12} (z_{m}^{+ +}, t_{k}) - φ_{12} (z_{m}^{+ -}, t_{k}) - φ_{12} (z_{m}^{- +}, t_{k}) + φ_{12} (z_{m}^{- -}, t_{k})

( 5.1B.34b )

φ_{13} (z_{m}^{}, t_{k}) = φ_{13} (z_{m}^{+ +}, t_{k}) - φ_{13} (z_{m}^{+ -}, t_{k}) - φ_{13} (z_{m}^{- +}, t_{k}) + φ_{13} (z_{m}^{- -}, t_{k})

( 5.1B.34c )

φ_{2} (z_{m}^{}, t_{k}) = φ_{2} (z_{m}^{+ +}, t_{k}) - φ_{2} (z_{m}^{+ -}, t_{k}) - φ_{2} (z_{m}^{- +}, t_{k}) + φ_{2} (z_{m}^{- -}, t_{k})

( 5.1B.34d )

The system of N equations (5.1B.33) is possible, with considering (5.1B.18) to (5.1B.21) and (5.1B.23) to (5.1B.32), to rewrite into the following matrix equation

\begin{array}{l} ([A_{11 C} (m, n)] + \frac{Δ t}{2 Δ z} [φ_{11 C} (m, n)]) {I (m, t_{k})} = {Δ t E_{}^{I} (m, t_{k - 1 / 2})} - [A_{12 C} (m, n)] {I (n, t_{k - 1})} - \\ - {A_{2} (m, t_{k})} + {A (m, t_{k - 1})} - \frac{Δ t}{2 Δ z} ([φ_{12 C} (m, n)] {I (m, t_{k - 1})} + \\ + [φ_{13 C} (m, n)] {\int_{0}^{t_{k - 1}} I (m, t) d t} + {φ_{2} (m, t_{k})} + {φ (m^{+}, t_{k - 1})} - {φ (m^{-}, t_{k - 1})}) \end{array}

( 5.1B.35 )

where

φ_{11 C} (m, n) = φ_{11 C} (m^{+}, n^{+}) - φ_{11 C} (m^{+}, n^{-}) - φ_{11 C} (m^{-}, n^{+}) + φ_{11 C} (m^{-}, n^{-})

( 5.1B.36a )

φ_{12 C} (m, n) = φ_{12 C} (m^{+}, n^{+}) - φ_{12 C} (m^{+}, n^{-}) - φ_{12 C} (m^{-}, n^{+}) + φ_{12 C} (m^{-}, n^{-})

( 5.1B.36b )

φ_{13 C} (m, n) = φ_{13 C} (m^{+}, n^{+}) - φ_{13 C} (m^{+}, n^{-}) - φ_{13 C} (m^{-}, n^{+}) + φ_{13 C} (m^{-}, n^{-})

( 5.1B.36c )

φ_{2} (m, n) = φ_{2} (m^{+}, n^{+}) - φ_{2} (m^{+}, n^{-}) - φ_{2} (m^{-}, n^{+}) + φ_{2} (m^{-}, n^{-})

( 5.1B.36d )

In (5.1B.35) we denote the matrix of the size NxN and Nx1 by square and brace brackets, respectively. It is apparent that the left side of the equation (5.1B.35) contains only the unknown currents at the time instants t=t_k, however, the right-side contains the known currents at time instants t±t_k-1. The algorithm can start with the assumption {I(m, t₀)}={0} and computing {I(m, t₁)}. When the current are computed {I(m,t₁)}, then it is possible to compute {I(m,t₂)} and so on. Further, it should be noted, that it is necessary to solve the inverse matrix. However, this one does not depend on time and it is spare. Thus, the inverse matrix is computed only once.

Using the implicit algorithm is demonstrated in the layer A on the analysis of the wire dipole.

Numerical model of antenna excitation

Let’s go back to the excitation of our wire antenna, and discus the appropriate numerical model of the excitation. Let’s suppose that the feeding ports of our antenna are located in the position of the current cells z₁, z₂, …, z_Nof our discretized wire antenna (fig. 5.1B.1); denote this place by z_f. The length of the feeding port is equal to the length of the discretization segment. An antenna can generally work in a receiving or transmitting mode.

If the antenna works in the receiving mode, the plane wave electromagnetic wave incidents on antenna’s surface, and its transient dependence can be arbitrary (in our case it is defined by a Gaussian pulse modulated by a harmonic signal (5.1A.7)). Depending on the direction of the incident wave with the respect to antenna axis, the transient dependence of the incident wave at the current cells z₁, z₂, …, z_Nis delayed. The incident wave induces in the wire antenna a current. The current response at the location of the feeding port z_f can be recorded.

If the antenna works in the transmitting mode, the situation is analogical to the one described in chapter 4.1. In the transmitting mode the voltage source is connected to the feeding port of the antenna at z_f. This source evokes the intensity of the electric field at the feeding port (in our case the time dependence is described by the Gaussian pulse modulated by a harmonic signal). Since the excitation source is connected only at the location of the feeding port z_f, at the other current cells the intensity of the excitation field is equal to zero.