Multimediální učebnice

5.1 Modelování drátových antén v časové oblasti metodou momentů

Podrobnější popis

V této vrstvě bude odvozen implicitní algoritmus řešením soustavy rovnic (5.1A.1) až (5.1A.6) pro drátový dipól, který je umístěn podél osy z. Vzhledem k tomu, že v této soustavě rovnic vystupují pouze z-ové složky vektorového potenciálu a intenzity elektrického pole, nemá smysl složky vektorů do souřadných směrů rozlišovat; v dalším textu můžeme dolní index z vynechat.

Při odvození výchozího vztahu pro implicitní algoritmus vyjděme z rovnice (5.1A.5), kterou je možné po zahrnutí okrajové podmínky (5.1A.6) přepsat do následující podoby

\frac{\partial A (z, t)}{\partial t} + \frac{\partial φ (z, t)}{\partial z} = E_{}^{I} (z, t)

( 5.1B.1 )

Nyní přistupme k prvnímu kroku řešení, tj. k aplikaci metody momentů na rovnici (5.1B.1). Rozdělme drátový dipól na N stejných segmentů délky Δz a označme konce segmentů souřadnicemi z₀, z₁, …, z_N+1 (obr. 5.1B.1). Středy segmentů označme z₀⁺, z₁⁺, …, z_N⁺, resp. z₁^-, z₂^-, …, z_N+1^-. Pro expanzi rozložení proudu na drátovém dipólu v prostoru použijeme konstantní bázové funkce: v oblasti proudové buňky (obr. 5.1B.1), která je ohraničena souřadnicemi z_n⁺, z_n+1⁺ resp. z_n-1^-, z_n^-, uvažujme konstantní rozložení proudu. Zde je nutné připomenout, že na konci drátu proud nemá kam téct a je roven nule. V oblasti nábojové buňky ohraničené souřadnicemi z_n, z_n+1 uvažujeme konstantní rozložení nábojové hustoty.

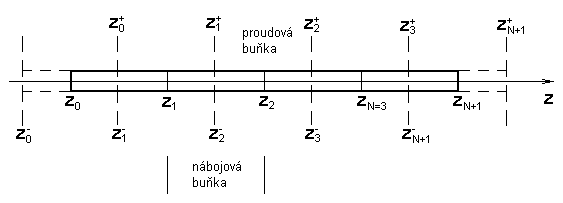Obr. 5.1B.1

Diskretizace drátového dipólu.

Konstantní bázové funkce v oblasti proudové buňky definujeme následujícím předpisem:

f_{n} = {\begin{cases} 1 z_{n} - \frac{Δ z}{2} \leq z \leq z_{n} + \frac{Δ z}{2} \\ 0 j i n a k \end{cases}

( 5.1B.2 )

Pomocí těchto bázových funkcí a časově závislých neznámých proudových koeficientů I_n(t) časoprostorové rozložení proudu ve vztahu (5.1A.1) může být rozepsáno

I (z, t) \approx \sum_{n = 1}^{N} I_{n} (t) f_{n} (z)

( 5.1B.3 )

Nyní přistoupíme k disretizaci našeho problému v čase (krok 2). Časovou osu si rozdělíme do časových intervalů délky Δt a jednotlivé body na časové ose označme t_k=kΔt pro k = 0, 1, 2, …, ∞. V těchto časových okamžicích budeme vyčíslovat rozložení proudu na drátové anténě.

Dosazením (5.1B.3) do (5.1A.1) může být vektorový potenciál v bodě z_m a v čase t_k rozepsán v následující formě:

A (z_{m}, t_{k}) = \frac{μ}{4 π} \int_{ξ = - h}^{h} \frac{I (ξ, t_{n} - R (z_{m}, ξ) / c)}{\sqrt{a^{2} + {| z_{m} - ξ |}^{2}}} d ξ \approx \frac{μ_{0}}{4 π} \int_{ξ = - h}^{h} \frac{\sum_{n = 1}^{N} I_{n} (t_{n} - R (z_{m}, ξ) / c) f_{n} (ξ)}{\sqrt{a^{2} + {| z_{m} - ξ |}^{2}}} d ξ = \sum_{n = 1}^{N} I_{n} (t_{R k} (m, n)) κ (m, n)

( 5.1B.4 )

kde

κ (m, n) = \frac{μ}{4 π} \int_{ξ = z_{n} - \frac{Δ z}{2}}^{z_{n} - \frac{Δ z}{2}} \frac{d ξ}{\sqrt{a^{2} + {| z_{m} - ξ |}^{2}}} = \frac{μ}{4 π} {\ln [z_{m} - z_{n} + \frac{Δ z}{2} + \sqrt{{(z_{m} - z_{n} + \frac{Δ z}{2})}^{2} + a^{2}}] - \ln [z_{m} - z_{n} - \frac{Δ z}{2} + \sqrt{{(z_{m} - z_{n} - \frac{Δ z}{2})}^{2} + a^{2}}]}

( 5.1B.5 )

t_{R k} (m, n) = t_{k} - R (m, n) / c

( 5.1B.6 )

R (m, n) = \sqrt{a^{2} + {| z_{m} - z_{n} |}^{2}}

( 5.1B.7a )

R (m, n) = | z_{m} - z_{n} |

( 5.1B.7b )

Pro výpočet vzdálenosti $R (m, n)$ v (5.1B.6) může být použit buď přesný vztah (5.1B.7a), nebo přibližný (5.1B.7b), který zanedbává poloměr drátu a. Použití přibližného vztahu zvětšuje stabilitu implicitního algoritmu, avšak přibližný vztah je možné použit jen pokud délka časového kroku násobená rychlostí světla je mnohem větší než poloměr anténního vodiče, tj. cΔt>>a. Jinak klesá přesnost. Použití přibližného vztahu bylo zavedeno v [37] a v případě splnění uvedené podmínky je ho dobré používat. Zainteresovaný čtenář si může vyzkoušet vliv tohoto zanedbání na přesnost a stabilitu algoritmu.

Nyní přistoupíme k diskretizaci skalárního potenciálu (5.1A.2), kde neznámou je časoprostorové rozložení nábojové hustoty. Ta může být vypočtena pomocí rovnice kontinuity (5.1A.4), kterou můžeme přepsat do následující formy

σ (z, t) = - \int \frac{\partial I (z, t)}{\partial z} d t

( 5.1B.8 )

Dosazením časoprostorového rozložení proudu (5.1B.3) do (5.1B.8) a náhradou parciální derivace proudu dle proměnné z středovou diferencí, rovnice kontinuity (5.1B.8) může být po záměně derivace s integrací rozepsána

σ (z, t) \approx - \frac{\partial \sum_{n = 1}^{N} \int I_{n} (t) d t f_{n} (z)}{\partial z} \approx - \sum_{n = 0}^{N} \frac{\int I_{n + 1} (t) d t - \int I_{n} (t) d t}{Δ z} f_{n}^{+} (z)

( 5.1B.9 )

Vzhledem k tomu, že používáme konstantní bázové funkce (5.1B.3) pro prostorové rozložení proudu, parciální derivace dle proměnné z v (5.1B.9) nemohla být vypočtena přímo (derivace konstantní funkce je rovna nule), ale muselo být použito středové diferencování. Aby diferencování bylo regulérní, byly v (5.1B.9) započítány i integrály proudů dle času na konci drátového dipólu, které jsou rovny nule. V posledním kroku jsme v (5.1B.9) zaměnili bázové funkce: z prostorové aproximace proudu pomocí bázových funkcí f_n(z) jsme přešli k aproximace nábojové hustoty pomocí bázových funkcí f_n⁺(z).

Dosazením rovnice kontinuity (5.1B.9) do rovnice (5.1A.2) můžeme v bodě z_m⁺ a v čase t_k vyčíslit skalární potenciál

\begin{array}{l} φ (z_{m}^{+}, t_{k}) = - \frac{1}{4 π ε} \int_{ξ = - h}^{h} \frac{σ (ξ, t_{k} - R (z_{m}^{+}, ξ) / c)}{R (z_{m}^{+}, ξ)} d ξ \approx - \frac{1}{4 π ε} \int_{ξ = - h}^{h} \sum_{n = 0}^{N} \frac{\int_{0}^{t_{k} - R (z_{m}^{+}, ξ) / c} I_{n + 1} (t) d t - \int_{0}^{t_{k} - R (z_{m}^{+}, ξ) / c} I_{n} (t) d t}{Δ z} f_{n}^{+} (ξ) \frac{1}{R (z_{m}^{+}, ξ)} d ξ = \\ = \sum_{n = 1}^{N} \frac{\int_{0}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t κ (m^{+}, n^{+})}{Δ z} - \sum_{n = 1}^{N} \frac{\int_{0}^{t_{R k} (m^{+}, n^{-})} I_{n} (t) d t κ (m^{+}, n^{-})}{Δ z} = φ (z_{m}^{+ +}, t_{k}) - φ (z_{m}^{+ -}, t_{k}) \end{array}

( 5.1B.10 )

kde

t_{R k} (m^{\pm}, n^{\pm}) = t_{k} - R (m^{\pm}, n^{\pm}) / c

( 5.1B.11 )

R (m^{\pm}, n^{\pm}) = \sqrt{a^{2} + {| z_{m}^{\pm} - z_{n}^{\pm} |}^{2}}

( 5.1B.12a )

R (m^{\pm}, n^{\pm}) = | z_{m}^{\pm} - z_{n}^{\pm} |

( 5.1B.12b )

κ (m^{\pm}, n^{\pm}) = \frac{1}{4 π ε} \int_{ξ = z_{n}^{\pm} - \frac{Δ z}{2}}^{z_{n}^{\pm} - \frac{Δ z}{2}} \frac{d ξ}{\sqrt{a^{2} + {| z_{m}^{\pm} - ξ |}^{2}}} = \frac{1}{4 π ε} {\ln [z_{m}^{\pm} - z_{n}^{\pm} + \frac{Δ z}{2} + \sqrt{{(z_{m}^{\pm} - z_{n}^{\pm} + \frac{Δ z}{2})}^{2} + a^{2}}] - \ln [z_{m}^{\pm} - z_{n}^{\pm} - \frac{Δ z}{2} + \sqrt{{(z_{m}^{\pm} - z_{n}^{\pm} - \frac{Δ z}{2})}^{2} + a^{2}}]}

( 5.1B.13 )

Zde, podobně jako v případě výpočtu vektorového potenciálu, je možné použit pro výpočet vzdálenosti $R (m^{\pm}, n^{\pm})$ v (5.1B.11) buď přesný (5.1B.12a), nebo přibližný výpočet (5.1B.12b). Důvody a podmínka jsou zde stejné jako v případě výpočtu vektorového potenciálu.

Obdobně může být vyjádřen skalární potenciál v bodě z_m^- a v čase t_k

φ (z_{m}^{-}, t_{k}) = φ (z_{m}^{- +}, t_{k}) - φ (z_{m}^{- -}, t_{k})

( 5.1B.14 )

Aby mohly být vyčísleny vztahy (5.1B.10) a (5.1B.14), je nutné vypočítat integrál proudu dle času. Integrál může být vypočten pomocí různých numerických integračních pravidel. My zvolíme lichoběžníkovou metodu, protože je jednoduchá na implementaci a poskytuje uspokojivou přesnost. Numericky je možné integrál proudu v intervalu 0 až t_k, za předpokladu ekvidistantního dělení intervalu vyčíslit jako

\int_{0}^{t_{k}} I (t) d t \approx Δ t [\frac{I (t_{0} = 0)}{2} + \sum_{l = 1}^{k - 1} I (t_{l}) + \frac{I (t_{k})}{2}]

( 5.1B.15 )

Nyní se vraťme k rovnici (5.1B.1) a diskretizujme ji. První parciální derivaci vektorové potenciálu dle času aproximujeme středovou diferencí prvního řádu. Tímto diferencováním je parciální derivace vektorové potenciálu vyčíslena v bodě z_ma v čase t_k-1/2. Aby náš výpočet byl dostatečně přesný, musíme v tomto bodě a čase vypočítat i parciální derivaci skalárního potenciálu dle proměnné z . Toho docílíme opětovným použitím středového diferencování pro skalární potenciál v bodech z_m⁺ a z_m^- ve dvou časech t_k a t_k-1. Průměr těchto dvou středových diferencí je vlastně numericky vyčíslená derivace skalárního potenciálu v bodě z_mv čase t_k-1/2. Samozřejmě budicí impuls musí být také vyčíslen ve stejném bodě a čase jako vektorový potenciál, tj. v bodě z_ma čase t_k-1/2. Po těchto krocích můžeme (5.1B.1) přepsat do následujícího tvaru:

\frac{A (z_{m}, t_{k}) - A (z_{m}, t_{k - 1})}{Δ t} + \frac{1}{2 Δ z} (φ (z_{m}^{+}, t_{k}) - φ (z_{m}^{-}, t_{k}) + φ (z_{m}^{+}, t_{k - 1}) - φ (z_{m}^{-}, t_{k - 1})) = E_{}^{I} (z, t_{k - 1 / 2})

( 5.1B.16 )

Přepsáním členů v (5.1B.16) dostáváme

\begin{array}{l} A (z_{m}, t_{k}) + \frac{Δ t}{2 Δ z} (φ (z_{m}^{+}, t_{k}) - φ (z_{m}^{-}, t_{k})) = Δ t E_{}^{I} (z, t_{k - 1 / 2}) + A (z_{m}, t_{k - 1}) \\ - \frac{Δ t}{2 Δ z} (φ (z_{m}^{+}, t_{k - 1}) - φ (z_{m}^{-}, t_{k - 1})) \end{array}

( 5.1B.17 )

Vektorový potenciál na levé straně rovnice (5.1B.17) vypočtený dle (5.1B.4) může být rozepsán jako

A (z_{m}, t_{k}) = A_{1} (z_{m}, t_{k}) + A_{2} (z_{m}, t_{k})

( 5.1B.18 )

kde

A_{1} (z_{m}, t_{k}) = \sum_{n = 1}^{N} I_{n} (t_{R k} (m, n)) κ (m, n) p r o t_{R k} (m, n) > t_{k - 1}

( 5.1B.19a )

A_{2} (z_{m}, t_{k}) = \sum_{n = 1}^{N} I_{n} (t_{R k} (m, n)) κ (m, n) p r o t_{R k} (m, n) \leq t_{k - 1}

( 5.1B.19b )

Pro vyčíslení A₁(z_m, t_k) jsou uváženy v sumě jen příspěvky proudů ve zpožděném čase t_Rk(m, n)> t_k-1, tedy proudy neznámé. V případě vyčíslení A₂(z_m, t_k) uvažujeme jen příspěvky proudů v čase t_Rk(m, n)≤ t_k-1, tj. proudy známé. Neznámý proud v čase t_Rk(m, n)v intervalu t_k-1 až t_kmůže být vyčíslen jako

I (t_{R k} (m, n)) = \frac{R (z_{m}, z_{n})}{c} I (t_{k - 1}) + (1 - \frac{R (z_{m}, z_{n})}{c}) I (t_{k})

( 5.1B.20 )

Dosazením (5.1B.20) do (5.1B.19a) může být A₁(z_m, t_k) rozepsáno pomocí neznámého a známého proudu v časech t_kresp. t_k-1

A_{1} (z_{m}, t_{k}) = A_{11} (z_{m}, t_{k}) + A_{12} (z_{m}, t_{k})

( 5.1B.21 )

kde

A_{11} (z_{m}, t_{k}) = \sum_{n = 1}^{N} (1 - \frac{R (z_{m}, z_{n})}{c Δ t}) κ (m, n) I_{n} (t_{k}) = \sum_{n = 1}^{N} A_{11 C} (m, n) I_{n} (t_{k})

( 5.1B.22a )

A_{12} (z_{m}, t_{k}) = \sum_{n = 1}^{N} \frac{R (z_{m}, z_{n})}{c Δ t} κ (m, n) I_{n} (t_{k}) = \sum_{n = 1}^{N} A_{12 C} (m, n) I_{n} (t_{k})

( 5.1B.22b )

Jen člen A₁₁(z_m, t_k) obsahuje neznámé proudy v čase t_k.

Nyní zaměřme pozornost na zbytek levé strany rovnice (5.1B.17), tj. na skalární potenciál (5.1B.10). Ten může být v bodě z_m⁺ vyčíslen jako

φ (z_{m}^{+}, t_{k}) = φ (z_{m}^{+ +}, t_{k}) - φ (z_{m}^{+ -}, t_{k})

( 5.1B.23 )

kde členy na pravé straně (5.1B.23) mohou být rozepsány jako vektorový potenciál (5.1B.18). Zaměřme naši pozornost na první člen

φ (z_{m}^{+ +}, t_{k}) = φ_{1} (z_{m}^{+ +}, t_{k}) + φ_{2} (z_{m}^{+ +}, t_{k})

( 5.1B.24 )

kde

\begin{array}{l} φ_{1} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \int_{0}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t \frac{κ (m^{+}, n^{+})}{Δ z} p r o t_{R k} (m^{+}, n^{+}) > t_{k - 1} \end{array}

( 5.1B.25a )

\begin{array}{l} φ_{2} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \int_{0}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t \frac{κ (m^{+}, n^{+})}{Δ z} p r o t_{R k} (m^{+}, n^{+}) \leq t_{k - 1} \end{array}

( 5.1B.25b )

Situace je analogická jako pro vektorový potenciál, avšak složitější, protože v (5.1B.25) vystupuje integrálu proudu podle času. Vzhledem k tomu, že jen člen φ₁(z_m⁺⁺, t_k) obsahuje neznámý proud v čase t_k, rozepišme integrál proudu přes interval 0 až t_Rk(m+, n+) v (5.1B.25a) na součet dvou integrálů

\begin{array}{l} φ_{1} (z_{m}^{+ +}, t_{k}) = φ_{1}' (z_{m}^{+ +}, t_{k}) + φ_{13} (z_{m}^{+ +}, t_{k}) \end{array}

( 5.1B.26 )

kde

\begin{array}{l} φ_{1}' (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \int_{t_{k - 1}}^{t_{R k} (m^{+}, n^{+})} I_{n} (t) d t \frac{κ (m^{+}, n^{+})}{Δ z} \end{array}

( 5.1B.27a )

\begin{array}{l} φ_{13} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{κ (m^{+}, n^{+})}{Δ z} \int_{0}^{t_{k - 1}} I_{n} (t) d t = \sum_{n = 1}^{N} φ_{13 C} (m^{+}, n^{+}) \int_{0}^{t_{k - 1}} I_{n} (t) d t \end{array}

( 5.1B.27b )

Člen φ₁₃(z_m⁺⁺, t_k) (5.1B.27b) může být jednoduše vyčíslen, protože obsahuje známé hodnoty proudů, avšak člen φ₁’(z_m⁺⁺, t_k) obsahuje neznámý proud v okamžiku v čase t_k. Proto dále rozepišme φ₁’(z_m⁺⁺, t_k) pomocí lichoběžníkového pravidla pro numerický výpočet integrálu v intervalu t_k-1 až t_Rk(m+, n+) a dále vztahů (5.1B.18) a (5.1B.20)

\begin{array}{l} φ_{1}' (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{Δ t}{2} (\frac{t_{R k} (m^{+}, n^{+}) - t_{k - 1}}{Δ t}) (I_{n} (t_{R k} (m^{+}, n^{+})) + I_{n} (t_{k - 1})) \frac{κ (m^{+}, n^{+})}{Δ z} = \\ = \sum_{n = 1}^{N} \frac{Δ t}{2} (1 - \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t}) [I_{n} (t_{k - 1}) \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t} + (1 - \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t}) I_{n} (t_{k}) + I_{n} (t_{k - 1})] \frac{κ (m^{+}, n^{+})}{Δ z} = \\ = φ_{11} (z_{m}^{+ +}, t_{k}) + φ_{12} (z_{m}^{+ +}, t_{k}) \end{array}

( 5.1B.28 )

kde

\begin{array}{l} φ_{11} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{Δ t}{2 Δ z} {(1 - \frac{R (z_{m}^{+}, z_{m}^{+})}{c Δ t})}^{2} κ (m^{+}, n^{+}) I_{n} (t_{k}) = \sum_{n = 1}^{N} φ_{11 C} (m^{+}, n^{+}) I_{n} (t_{k}) \end{array}

( 5.1B.29a )

\begin{array}{l} φ_{12} (z_{m}^{+ +}, t_{k}) = \sum_{n = 1}^{N} \frac{Δ t}{2 Δ z} (1 - \frac{R^{2} (z_{m}^{+}, z_{m}^{+})}{c^{2} Δ t^{2}}) κ (m^{+}, n^{+}) I_{n} (t_{k - 1}) = \sum_{n = 1}^{N} φ_{12 C} (m^{+}, n^{+}) I_{n} (t_{k - 1}) \end{array}

( 5.1B.29b )

Nyní už jen člen φ₁₁(z_m⁺⁺, t_k) obsahuje neznámý proud v čase t_k. Tento člen může být jednoduše vyjádřen dle (5.1B.29a). Vztah (5.1B.24) může být s uvážením (5.1B.25) až (5.1B.29) vyjádřen následovně:

φ (z_{m}^{+ +}, t_{k}) = φ_{11} (z_{m}^{+ +}, t_{k}) + φ_{12} (z_{m}^{+ +}, t_{k}) + φ_{13} (z_{m}^{+ +}, t_{k}) + φ_{2} (z_{m}^{+ +}, t_{k})

( 5.1B.30 )

Analogicky můžeme postupovat v případě vyčíslení φ (z_m^+-, t_k)

φ (z_{m}^{+ -}, t_{k}) = φ_{11} (z_{m}^{+ -}, t_{k}) + φ_{12} (z_{m}^{+ -}, t_{k}) + φ_{13} (z_{m}^{+ -}, t_{k}) + φ_{2} (z_{m}^{+ -}, t_{k})

( 5.1B.31 )

resp. skalárního potenciálu φ(z_m^-, t_k).

φ (z_{m}^{-}, t_{k}) = φ (z_{m}^{- +}, t_{k}) - φ (z_{m}^{- -}, t_{k})

( 5.1B.14 )

kde

φ (z_{m}^{- +}, t_{k}) = φ_{11} (z_{m}^{- +}, t_{k}) + φ_{12} (z_{m}^{- +}, t_{k}) + φ_{13} (z_{m}^{- +}, t_{k}) + φ_{2} (z_{m}^{- +}, t_{k})

( 5.1B.32a )

φ (z_{m}^{- -}, t_{k}) = φ_{11} (z_{m}^{- -}, t_{k}) + φ_{12} (z_{m}^{- -}, t_{k}) + φ_{13} (z_{m}^{- -}, t_{k}) + φ_{2} (z_{m}^{- -}, t_{k})

( 5.1B.32b )

Členy na pravých stranách rovnic (5.1B.31) a (5.1B.32) mohou být obdobně jako členy na pravé straně pomocí rovnic (5.1B.24) až (5.1B.29) vytvořeny pouhou záměnou odpovídajících si indexů + a -, nebo obráceně.

Dosazením (5.1B.10), (5.1B.14), (5.1B.18) až (5.1B.21), (5.1B.24) až (5.1B.32) do levé strany rovnice (5.1B.17) a po přerovnání členů této rovnice dostáváme

\begin{array}{l} A_{11} (z_{m}, t_{k}) + \frac{Δ t}{2 Δ z} φ_{11} (z_{m}^{}, t_{k}) = Δ t E_{}^{I} (z_{m}, t_{k - 1 / 2}) - A_{12} (z_{m}, t_{k}) - A_{2} (z_{m}, t_{k}) + A (z_{m}, t_{k - 1}) - \\ - \frac{Δ t}{2 Δ z} (φ_{12} (z_{m}^{}, t_{k}) + φ_{13} (z_{m}^{}, t_{k}) + φ_{2} (z_{m}^{}, t_{k}) + φ (z_{m}^{+}, t_{k - 1}) - φ (z_{m}^{-}, t_{k - 1})) \end{array}

( 5.1B.33 )

kde

φ_{11} (z_{m}^{}, t_{k}) = φ_{11} (z_{m}^{+ +}, t_{k}) - φ_{11} (z_{m}^{+ -}, t_{k}) - φ_{11} (z_{m}^{- +}, t_{k}) + φ_{11} (z_{m}^{- -}, t_{k})

( 5.1B.34a )

φ_{12} (z_{m}^{}, t_{k}) = φ_{12} (z_{m}^{+ +}, t_{k}) - φ_{12} (z_{m}^{+ -}, t_{k}) - φ_{12} (z_{m}^{- +}, t_{k}) + φ_{12} (z_{m}^{- -}, t_{k})

( 5.1B.34b )

φ_{13} (z_{m}^{}, t_{k}) = φ_{13} (z_{m}^{+ +}, t_{k}) - φ_{13} (z_{m}^{+ -}, t_{k}) - φ_{13} (z_{m}^{- +}, t_{k}) + φ_{13} (z_{m}^{- -}, t_{k})

( 5.1B.34c )

φ_{2} (z_{m}^{}, t_{k}) = φ_{2} (z_{m}^{+ +}, t_{k}) - φ_{2} (z_{m}^{+ -}, t_{k}) - φ_{2} (z_{m}^{- +}, t_{k}) + φ_{2} (z_{m}^{- -}, t_{k})

( 5.1B.34d )

Soustavu N rovnic (5.1B.33) je možné s uvážením (5.1B.18) až (5.1B.21) a (5.1B.23) až (5.1B.32) přepsat do maticové rovnice

\begin{array}{l} ([A_{11 C} (m, n)] + \frac{Δ t}{2 Δ z} [φ_{11 C} (m, n)]) {I (m, t_{k})} = {Δ t E_{}^{I} (m, t_{k - 1 / 2})} - [A_{12 C} (m, n)] {I (n, t_{k - 1})} - \\ - {A_{2} (m, t_{k})} + {A (m, t_{k - 1})} - \frac{Δ t}{2 Δ z} ([φ_{12 C} (m, n)] {I (m, t_{k - 1})} + \\ + [φ_{13 C} (m, n)] {\int_{0}^{t_{k - 1}} I (m, t) d t} + {φ_{2} (m, t_{k})} + {φ (m^{+}, t_{k - 1})} - {φ (m^{-}, t_{k - 1})}) \end{array}

( 5.1B.35 )

kde

φ_{11 C} (m, n) = φ_{11 C} (m^{+}, n^{+}) - φ_{11 C} (m^{+}, n^{-}) - φ_{11 C} (m^{-}, n^{+}) + φ_{11 C} (m^{-}, n^{-})

( 5.1B.36a )

φ_{12 C} (m, n) = φ_{12 C} (m^{+}, n^{+}) - φ_{12 C} (m^{+}, n^{-}) - φ_{12 C} (m^{-}, n^{+}) + φ_{12 C} (m^{-}, n^{-})

( 5.1B.36b )

φ_{13 C} (m, n) = φ_{13 C} (m^{+}, n^{+}) - φ_{13 C} (m^{+}, n^{-}) - φ_{13 C} (m^{-}, n^{+}) + φ_{13 C} (m^{-}, n^{-})

( 5.1B.36c )

φ_{2} (m, n) = φ_{2} (m^{+}, n^{+}) - φ_{2} (m^{+}, n^{-}) - φ_{2} (m^{-}, n^{+}) + φ_{2} (m^{-}, n^{-})

( 5.1B.36d )

Hranatými závorkami v (5.1B.35) označujeme matici velikosti NxN a složenými závorkami vektor o velikosti Nx1. Z (5.1B.35) je zřejmé, že levá strana rovnice obsahuje jen neznámé proudy v časových okamžicích t=t_k, kdežto pravá strana obsahuje známé proudy v časech t±t_k-1. Algoritmus může začít s předpokladem, že {I(m, t₀)}={0} a výpočtem {I(m, t₁)}. Když jsou vypočteny proudy {I(m,t₁)}, tak pak je možné počítat {I(m,t₂)}, atd. Dále je nutné poznamenat, že při řešení soustavy rovnic (5.1B.35) je nutno jednou řešit inverzní matici (její členy jsou časově nezávislé). Výhodou je, že matice je řídká.

Použití implicitního algoritmu je demonstrováno ve vrstvě A na analýze drátového dipólu.

Numerický model buzení antén

Vraťme se ještě k buzení naší drátové antény a diskutujme, jak můžeme nejvhodněji vytvořit numerický model buzení. Jakákoliv anténa může obecně pracovat buď v přijímacím, nebo ve vysílacím módu. Předpokládejme, že svorky naší antény jsou umístěny v jedné z proudových buněk z₁, z₂, …, z_N naší diskretizované drátové antény (obr. 5.1B.1); toto místo označme z_f. Vzdálenost svorek antény je rovna délce diskretizačního elementu.

Pokud anténa pracuje v přijímacím módu, na její povrch dopadá rovinná elektromagnetická vlna, jejíž časový průběh může mít obecný charakter; v našem případě je definována Gaussovým impulsem modulovaný harmonickým signálem (5.1A.7). V závislosti na směru dopadu příchozí vlny vzhledem k ose antény je časový průběh dopadající vlny v proudových buňkách naší struktury z₁, z₂, …, z_N časově zpožděn. Dopadající vlna indukuje v drátové anténě proud. Odezva proudu v místě svorek antény může být zaznamenána v z_f.

Pokud požadujeme, aby anténa pracovala ve vysílacím módu, je situace analogická situaci, která byla popsána v kapitole 4.1. Ve vysílacím módu je napěťový zdroj připojen ke svorkám antény v místě z_f. Tento zdroj vyvolá budicí intenzitu elektrického pole na svorkách antény (v našem případě je časový průběh dán Gaussovým impulsem modulovaný harmonickým signálem). Vzhledem k tomu, že budicí zdroj je připojen jen v jednom místě (z_f), v ostatních proudových buňkách bude intenzita budicího pole rovna nule.