Multimedia textbook

6.1 Analysis of frequency selective surfaces

Basic theory

In this paragraph, reflection coefficient and transmission coefficient are computed for an infinite periodic frequency selective surface. The attention is turned to the surface consisting of rectangular elements (metallic, slot). First, the surface is assumed to be fabricated from such dielectrics, which properties are identical with surrounding. At the end, a brief note on the analysis of real substrates is provided.

Numeric analysis of frequency selective surfaces

There are two approaches to the analysis of frequency selective surfaces. The first one is based on the method of induced electromotoric forces and enables to analyze surfaces of both the finite extent and the infinite one (in most cases, the method is applied to infinite structures). Analysis by the method of induced electromotoric forces is not described here; readers interested can find more information in [17].

Spectral domain moment method is the second way of analyzing frequency selective surfaces [18]. We concentrate to this method only.

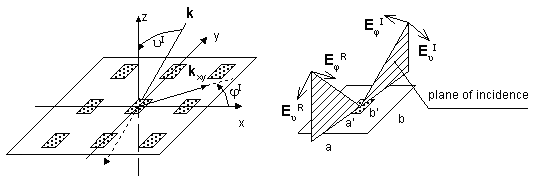
Fig. 6.1A.1

Coordinate system for the analysis of a frequency selective surface (left). An elementary cell of the dimensions a, b (right).

Metallic elements

We assume a periodic surface as depicted in fig. 6.1A.1. The surface is illuminated by a plane wave. Projection of wave vector k to the plane of the surface is denoted by k_xy. Electric filed intensity of incident wave can be expressed then as follows:

E^{I} = E_{0} \exp [+ j (α_{0} x + β_{0} y)]

( 6.1A.1 )

Here, α₀, β₀ are negative projections of wave vector of incident wave to the directions of coordinate axes x and y (the exponential term exp(+jkr) is assumed for increasing phase in the direction of propagation). Projections of wave vector in the described coordinate system are given as follows:

α_{0} = k \sin (ϑ) \cos (φ)

β_{0} = k \sin (ϑ) \sin (φ)

The symbol E₀ denotes electric-field intensity vector in the origin of the coordinate system and k is free-space wave number.

In general, the incident wave is of both the parallel polarization and the perpendicular one. If field intensity of the incident wave is expressed in spherical coordinate system (fig. 6.1A.1), then components E_ϑ^I and E_φ^I represent directly the parallel component and the perpendicular one.

If frequency selective surface is going to be analyzed, components of electric field intensity in the plane xy have to be known. We can evaluate them re-computing E_ϑ^I and E_φ^I as follows:

[\begin{matrix} E_{x}^{I} \\ E_{y}^{I} \end{matrix}] = [\begin{matrix} \sin (ϑ) \cos (φ) & - \sin (φ) \\ \sin (ϑ) \sin (φ) & \cos (φ) \end{matrix}] [\begin{matrix} E_{ϑ}^{I} \\ E_{φ}^{I} \end{matrix}]

( 6.1A.2 )

Due to the periodicity of the surface, all the necessary quantities (electric field intensity, current density) in the plane xy can be expressed using Fourier series. Using Fourier expansion, density of electric current J [A/m] on metallic element is expressed:

J = \sum_{m = - M}^{M} \sum_{n = - N}^{N} J (α_{m}, β_{n}) \exp [+ j (α_{m} x + β_{n} y)]

( 6.1A.3 )

where

α_{n} = α_{0} + \frac{2 π}{a} m, β_{n} = β_{0} + \frac{2 π}{b} n

( 6.1A.4 )

are spatial frequencies. Those spatial frequencies are a spatial analogy to the temporal angular frequency ω, which are used for temporal analysis of signals. The only difference is hidden in the fact that time period T corresponds to spatial periods a and b.

Coefficients of Fourier series can be obtained by integrating current densities over the whole surface of a cell (inverse Fourier transform)

J (α_{m}, β_{n}) = \frac{1}{a b} \iint_{p l o c h a b u ň k y} J (x, y) \exp [- j (α_{m} x + β_{n} y)]

( 6.1A.5 )

In analogy to current density, Fourier series can express arbitrary periodic quantity. We do that in the next part, where a plane wave excitation of a selective surface is expressed in the spectral domain (i.e., in the domain of spatial frequencies). Determination of reflective properties of the selective surface is the aim of the computation.

Problem formulation

Fig. 6.1A.2

Frequency selective surface (reflected and transmitted wave)

Assume a plane wave falling to a frequency selective surface under angles (ϑ, φ). This wave excites currents in metallic elements, which form a scattered field E^S.

Whereas the magnitude (not the phase) of the intensity of incident wave E^I is constant over the whole elementary cell, the magnitude of the intensity of the scattered wave E^S is different in the different points of the cell. Relation between E^S and E^I changes according to the surface impedance in a given point. For the surface of conductive elements, we get

E^{I} + E^{S} = \frac{J}{γ}

( 6.1A.6 )

Here, γ [S.m^-1] is electric conductivity of elements. Assuming the electric conductivity of metallic elements to be perfect, the right-hand side of (6.1A.6) approaches zero, and we get

E^{I} + E^{S} = 0

( 6.1A.7 )

Intensity of scattered electric field E^S in a point determined by the position vector r can be evaluated from vector potential A

E^{S} (r) = - j ω μ {A + \frac{1}{k^{2}} \nabla [\nabla \cdot A (r)]}

( 6.1A.8 )

As a source of vector potential A, currents J induced by incident wave to metallic elements of selective surface can be considered. Contribution of current in r' to the potential in r is described by Green function G. For vector potential, we get

A (r) = \iint_{z d r o j e} G (r | r^{'}) J (r^{'}) d S^{'}

( 6.1A.9 )

In free space, Green function G is of the form

G = \frac{\exp (- j k | r - r^{'} |)}{4 π | r - r^{'} |}

( 6.1A.10 )

Combining relations (6.1A.9), (6.1A.8) and (6.1A.7), integral equation for space-domain electric field is obtained:

- j ω μ {\iint_{z d r o j e} G (r | r^{'}) \cdot J (r^{'}) d S^{'} + \frac{1}{k^{2}} \nabla [\nabla \cdot \iint_{z d r o j e} G (r | r^{'}) \cdot J (r^{'}) d S^{'}]} = - E^{I}

( 6.1A.11 )

Eqn. (6.1A.11) is solved in the domain of spatial frequencies. Eqn. (6.1A.11) is mapped to the spectral domain within two steps. First, eqn. (6.1A.8) is mapped by its rewriting to the component form and by expressing vector potential by Fourier series. That way, we get [19]

[\begin{matrix} E_{x}^{S} (α_{m}, β_{n}) \\ E_{z}^{S} (α_{m}, β_{n}) \end{matrix}] = - j ω μ [\begin{matrix} 1 - \frac{α_{m}^{2}}{k^{2}} & \frac{- α_{m} β_{n}}{k^{2}} \\ \frac{- α_{m} β_{n}}{k^{2}} & 1 - \frac{β_{n}^{2}}{k^{2}} \end{matrix}] [\begin{matrix} A_{x} (α_{m}, β_{n}) \\ A_{y} (α_{m}, β_{n}) \end{matrix}]

( 6.1A.12 )

In the second step, the relation is mapped to the domain of spatial frequencies (6.1A.9) [19]

A (α_{m}, β_{n}) = G (α_{m}, β_{n}) \cdot J (α_{m}, β_{n})

( 6.1A.13 )

Evaluating Fourier transform of the function (6.1A.10), we get [19] Green function in spectral domain

G (α_{m}, β_{n}) = \frac{- j}{2 \sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}}

( 6.1A.14 )

where the square-root of negative imaginary part is assumed only.

Combining (6.1A.13), (6.1A.14) and (6.1A.12), the final relation for electric field in spectral domain is obtained

- \frac{1}{2 ω ε} \sum_{m, n} [\begin{matrix} \frac{k^{2} - α_{m}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \\ \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{k^{2} - β_{n}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \end{matrix}] [\begin{matrix} J_{x} (α_{m}, β_{n}) \\ J_{y} (α_{m}, β_{n}) \end{matrix}] \exp [j (α_{m} x + β_{n} y)] = - [\begin{matrix} E_{x}^{I} (x, y) \\ E_{y}^{I} (x, y) \end{matrix}]

( 6.1A.15 )

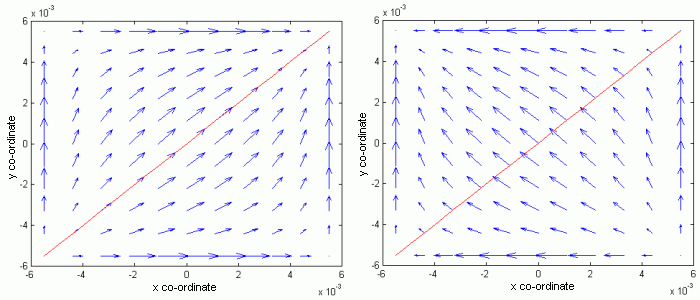
Problem solution

Solving the problem, an unknown current distribution in (6.1A.15) is approximated by the linear combination of properly chosen basis functions and unknown approximation coefficients. Such formal approximation is substituted into the solved eqn. (6.1A.15). Since the approximation of the solution does not meet the initial relation exactly, we respect this fact by introducing a residual function (residuum). Lower the residuum is, more accurate the approximation is. The residuum is minimized by Galerkin method (residuum is sequentially multiplied by as many basis functions as many unknown approximation coefficients is computed; that way, N linear algebraic equations for N unknown approximation coefficients is obtained).

There are two approaches for choosing basis functions. The first one exploits basis functions, which are non-zero over the whole analyzed area. Functions are elected to physically represent standing waves of a current on an element.

The second approach divides the analyzed region to sub-regions, where current is approximated in terms of basis functions, which functional value is non-zero over a given sub-region only. This approach is advantageous in simple analysis of selective surfaces consisting of arbitrarily shaped elements.

Here, we concentrate on the first group of basis functions only. As basis functions, harmonic functions are used (first approach, the layer B), and a combination of harmonic functions and Chebyshev polynomials is exploited (second approach, the layer B).

A more detailed description of the above-given basis functions for solving (6.1A.15) is introduced in the layer B. Here, obtained results are presented only.

Harmonic basis functions

Assume a frequency selective surface consisting of rectangular perfectly conductive elements of the dimensions a' and b'. If current distribution over an element is approximated in terms of harmonic basis functions, we obtain for the mode (1, 1) for the parallel polarization such current distribution, which is depicted in fig. 6.1A.3a, and for the perpendicular polarization, the distribution from fig. 6.1A.3b is obtained

Fig. 6.1A.3

Directional field of current density of the mode (1,1)
a) for parallel polarization
b) for perpendicular one.
The cell is of dimensions a = b = 12mm, the metallic element is of dimensions a' = b' = 12mm; f=10GHz, ϑ = 1°, φ = 45°, d = 1.5mm, ε_r = 3.7. Magnitude of marginal currents was increased with respect to reality. Plane of incidence is depicted in red.

Combination of harmonic functions and Chebyshev polynomials

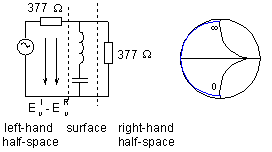
Fig. 6.1A.4

Equivalent circuit of selective surface in frequency domain; surface consist of metallic elements (left); ϑ = φ = 0. Directivity factor in Smith chart (right).

In contrast to purely harmonic basis functions, the function cosine is replaced by Chebyshev polynomial, which is of infinite magnitude at the edges of the element. That way, strong currents flowing along edges are correctly modeled.

An equivalent circuit can describe behavior of frequency selective surfaces, which consist of metallic elements, where inductances of elements together with capacitances among ends of elements create a serial resonant circuit (fig. 6.1A.4).

Reflection coefficient r (see fig. 6.1A.4) is evaluated according to

P^{T} = P^{I} [1 - {| ρ |}^{2}]

( 6.1A.16 )

Here, P^I is power of incident wave and P^T denotes power of wave, which was transmitted by the surface to the right-hand half-space. Resistance 377 Ω models free space in front of the surface (left) and behind the surface (right).

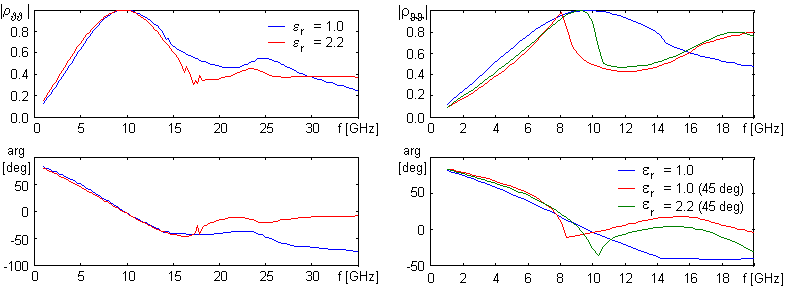
Fig. 6.1A.5

Surface of rectangular elements, tuned for 10 GHz, parallel polarization
a) normal incidence ϑ = 0°, φ = 90°
b) unnormal incidence ϑ = 45°, φ = 90°

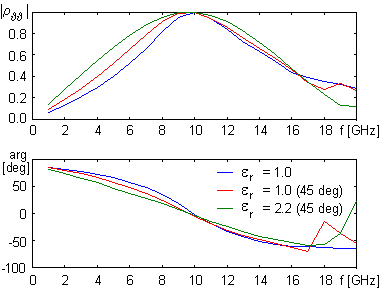
Frequency course of reflection coefficient of the surface for parallel polarization is depicted in fig. 6.1A.5. Considering the surface without dielectrics, (b = 21 mm, a = 7.5 mm, b' = 19.75 mm, a' = 1.5 mm), there is a break of the steepness of the reflection coefficient course around 14.3 GHz; this phenomenon is caused by the excitation of the first parasitic mode (grating lobe).

Adding dielectrics and modifying dimensions (b = 17 mm, a = 7.5 mm, b' = 15.75 mm, a' = 1.5 mm, height of the substrate d = 1.57 mm) causes a small decrease of the selectivity on one hand, but the stability of tuning for un-normal incidence is increased on the other hand (see fig. 6.1A.5b). Further increase of the stability of reflection coefficient with respect to the angle of incidence can be reached by adding an upper dielectric layer. Thanks to the dielectrics, cell dimensions are smaller and parasitic modes are excited at higher frequencies (17.6 GHz). In fig. 6.1A.5b, no significant effect of this mode can be observed.

Both the normal incidence and the un-normal one excite parasitic resonance at higher frequencies. At frequencies, which are higher than the frequency of the first parasitic mode, the course of reflection coefficient does not express the total intensity of the reflected wave, but only the intensity of the basic mode (0,0).

Considering perpendicular polarization of incident wave (in contrast to parallel one), reflection coefficient is nearly independent on the angle of incidence (see fig. 6.1A.6). If a surface without dielectrics is considered, dimensions b = 21 mm, a = 7.5 mm, b' = 19.75 mm, a' = 1.5 mm, are assumed., If dielectrics is considered, dimensions b = 17 mm, a = 7.5 mm, b' = 15.75 mm, a' = 1.5 mm and the height of the substrate d = 1.57 mm are assumed.

Fig. 6.1A.6

Surface of rectangular elements, tuned for 10 GHz, unnormal incidence, ϑ = 45°, φ = 0°, perpendicular polarization.

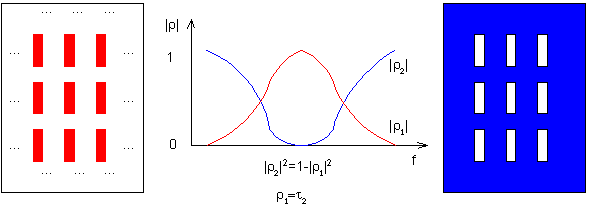
Slot elements

In contrast to the surfaces of metallic elements, frequency selective surfaces of slots exhibit an opposite dependency of reflection coefficient, i.e. they behave as a band-stop filter. If no dielectrics and a single metallic layer are assumed, then slot surfaces are true complements of metallic-element surfaces.

surface 1

surface 2

Fig. 6.1A.7

Complementary behavior of slot surfaces and metallic-element ones. Reflection coefficient of metallic-element surface (1) equals to transmission coefficient of slot surface (2).

Now, we turn our attention to the derivation of equations for magnetic intensity over the aperture of slot surface in spectral domain. Considering the case without dielectrics and with a single metallic layer, duality principle can be applied: in (6.1A.15), we exchange E with H, ε with μ, J with J_M

- \frac{1}{2 ω μ} \sum_{m, n} [\begin{matrix} \frac{k^{2} - α_{m}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \\ \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{k^{2} - β_{n}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \end{matrix}] [\begin{matrix} 2 J_{x}^{M +} (α_{m}, β_{n}) \\ 2 J_{y}^{M +} (α_{m}, β_{n}) \end{matrix}] \exp [j (α_{m} x + β_{n} y)] = - [\begin{matrix} 2 H_{x}^{I} (x, y) \\ 2 H_{y}^{I} (x, y) \end{matrix}]

( 6.1A.17 )

Comparing (6.1A.17) and (6.1A.15), a certain inconsistency can be revealed: coefficient 2 appeared at magnetic current density and exciting magnetic intensity. Next to the duality principle, the following fact had to be considered:

Field radiated by electric currents of the metallic-element surface is not scattered by those elements, whereas magnetic currents in slots produce a field, which is scattered by the conductive plane [19]. In order to include the influence of the surrounding of the conductive plane, following steps have to be done:

Original electric currents are replaced by magnetic ones (flowing on the surface of the slot). Magnetic current density can be computed applying J_M⁺ = z × E_ap, where E_ap is electric field intensity in the aperture (similarly to electric current, even the magnetic conductor of a real thickness is flown by the current from one side only - from left one).
The slot is assumed to be filled in by perfect electric conductor (that way, an infinite continuous ground plane is obtained). This assumption does not change the situation any way because at the boundary of metal and air, the tangential components of electric field intensity are related by $E_{t}^{k o v} - E_{t}^{v z d u c h} = J_{M}^{+} \times (- z)$ , and field intensity in metal $E_{t}^{k o v} = 0$ is zero.
Mirror principle is applied, which converts the problem to free-space one (fig. 6.1A.8 right).

original problem when magnetic current introduced

extension of ground plane and considering left-hand half-space only

application of mirror principle

Fig. 6.1A.8

Explanation of equivalence principle

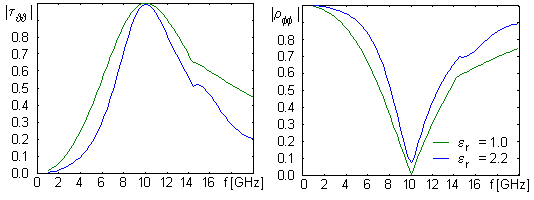
In analogy to metallic elements, dual formulation of transmission coefficient is possible τ.

In fig. 6.1A.9, an example for normal incidence of a wave to a frequency selective surface with slots in vacuum (b = 21 mm, a = 7.5 mm, b' = 19.75 mm, a' = 1.5 mm) and on dielectric substrate (b = 14 mm, a = 7.5 mm, b' = 13.25 mm, a' = 1.5 mm and the height of the substrate d = 1.57 mm) are given. Obviously, selectivity of transmission coefficient is better for dielectrics (in case of metallic-element surface, the situation was opposite). Next, influence of dielectrics is different compared to metallic-element surface, and therefore, slots are of different dimensions compared to metallic-element surface with dielectrics. Dielectrics even cause non-zero value of reflection coefficient on resonant frequency. Even here, parasitic modes appear.

Conclusion

The method of the analysis of frequency selective surfaces, given in this chapter, does not include the influence of dielectrics, but given examples do that [17]. Another way of the description of the influence of dielectrics can be found in [19].

Real applications use several sequentially lined selective surfaces. That way, selectivity can be significantly improved. Design of such surfaces is rather complicated.

Frequency selective surfaces can be modeled in commercial programs based on finite elements (HFSS) or on moment method (IE3D). In both cases, only a single element is analyzed thanks to the periodicity.

Designing frequency selective surfaces, physical basis of their behavior and limitations have to be known.

transmission

reflection

Fig. 6.1A.9

Surface of rectangular slots, tuned for 10 GHz, normal incidence ϑ = 0° φ = 90°, perpendicular polarization.