Multimediální učebnice

6.1 Analýza kmitočtově selektivních povrchů

Základní teorie

V tomto článku se budeme věnovat způsobu výpočtu koeficientu odrazu a koeficientu prostupu pro nekonečně rozlehlý periodický kmitočtově selektivní povrch. Zaměříme se přitom na povrch, sestávající se z obdélníkových elementů (kovových a štěrbinových). Nejdříve budeme předpokládat, že povrch je vyroben z dielektrického substrátu, který má stejné parametry jako prostředí, v němž je povrch umístěn. Na závěr se v poznámce zmíníme, jak lze analyzovat povrch v případě reálného substrátu (s parametry odlišnými od okolního prostředí).

Numerická analýza kmitočtově selektivních povrchů

Kmitočtově selektivní povrchy můžeme v podstatě analyzovat dvěma způsoby. První způsob vychází z metody indukovaných elektromotorických napětí a umožňuje analyzovat povrchy jak konečně tak nekonečně rozlehlé (nejčastěji se však používá pouze její varianta pro nekonečně rozlehlý případ). Analýza technikou indukovaných elektromotorických napětí zde nebude popisována, lze ji však nalézt v [17].

Druhý způsob, jak numericky analyzovat kmitočtově selektivní povrchy, vychází z momentové metody ve spektrální oblasti [18]. Na tuto metodu se soustředíme v našem článku.

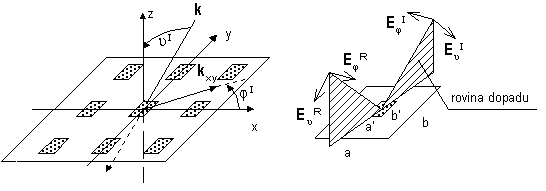
Obr. 6.1A.1

Souřadný systém pro analýzu kmitočtově selektivního povrchu (vlevo). Elementární buňka s rozměry a, b (vpravo).

Kovové elementy

Uvažujme periodický selektivní povrch podle obr. 6.1A.1. Na povrch dopadá rovinná vlna. Průmět vlnového vektoru k do roviny povrchu je označen k_xy. Elektrickou intenzitu dopadající vlny lze pak vyjádřit následovně:

E^{I} = E_{0} \exp [+ j (α_{0} x + β_{0} y)]

( 6.1A.1 )

Zde α₀, β₀ jsou záporné průměty vlnového vektoru dopadající vlny do směrů souřadných os x a y (v našem výkladu budeme totiž předpokládat znaménkovou konvenci exp(+jkr), kdy při postupu vlny ve směru šíření její fáze narůstá.). Pro průměty vlnového vektoru v zavedeném souřadném systému platí

α_{0} = k \sin (ϑ) \cos (φ)

β_{0} = k \sin (ϑ) \sin (φ)

Symbol E₀ značí vektor intenzity elektrického pole v počátku souřadného systému a k je vlnové číslo ve volném prostoru.

Dopadající vlna má obecně jak rovnoběžnou polarizaci tak polarizaci kolmou. Pokud vyjádříme intenzitu dopadající vlny v kulovém souřadném systému (viz obr. 6.1A.1), budou složky E_ϑ^I a E_φ^I představovat přímo rovnoběžnou složku a složku kolmou.

Pro následnou analýzu kmitočtově selektivního povrchu je nutné znát složky vektoru elektrické intenzity v rovině xy. Ty lze získat ze známých E_ϑ^I a E_φ^I následovně:

[\begin{matrix} E_{x}^{I} \\ E_{y}^{I} \end{matrix}] = [\begin{matrix} \sin (ϑ) \cos (φ) & - \sin (φ) \\ \sin (ϑ) \sin (φ) & \cos (φ) \end{matrix}] [\begin{matrix} E_{ϑ}^{I} \\ E_{φ}^{I} \end{matrix}]

( 6.1A.2 )

Protože je povrch periodický, můžeme všechny potřebné veličiny (intenzita elektrického pole, proudová hustota) v rovině xy vyjádřit pomocí Fourierovy řady. Pomocí Fourierova rozvoje nejprve vyjádříme hustotu elektrického proudu J [A/m] tekoucího na kovovém elementu:

J = \sum_{m = - M}^{M} \sum_{n = - N}^{N} J (α_{m}, β_{n}) \exp [+ j (α_{m} x + β_{n} y)]

( 6.1A.3 )

kde

α_{n} = α_{0} + \frac{2 π}{a} m, β_{n} = β_{0} + \frac{2 π}{b} n

( 6.1A.4 )

představují tzv. prostorové kmitočty. Tyto prostorové kmitočty jsou prostorovou analogií k časovému úhlovému kmitočtu ω, který používáme při časové analýze signálů. Rozdíl je pouze v tom, že časové periodě T nyní odpovídají prostorové periody a a b.

Koeficienty Fourierovy řady lze získat integrací proudové hustoty přes plochu buňky (jedná se o zpětnou Fourierovu transformaci, s níž se setkáváme např. při časové analýze signálů)

J (α_{m}, β_{n}) = \frac{1}{a b} \iint_{p l o c h a b u ň k y} J (x, y) \exp [- j (α_{m} x + β_{n} y)]

( 6.1A.5 )

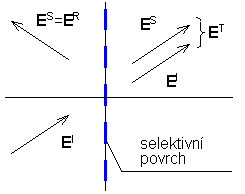
Obdobně jako proudovou hustotu lze pomocí Fourierovy řady vyjádřit libovolnou veličinu, která je periodická. To je případ dalšího odstavce, v němž bude ve spektrální oblasti (tj. v oblasti prostorových kmitočtů) vyjádřeno buzení kmitočtově selektivního povrchu rovinnou vlnou. Našim cílem přitom bude určit odrazné vlastnosti selektivního povrchu.

Formulace problému

Uvažujme rovinnou vlnu, která dopadá na kmitočtově selektivní povrch pod úhly (ϑ, φ). Tato vlna vybudí v kovových elementech proudy, které vytvoří tzv. rozptýlené pole E^S.

Obr. 6.1A.2

Kmitočtově selektivní povrch (odražená a prostupující vlna)

Zatímco velikost (ne fáze) intenzity dopadající vlny E^I je konstantní po celé ploše elementární buňky, velikost intenzity vlny rozptýlené E^S je v různých místech buňky různá. Vztah mezi E^S a E^I se přitom mění podle toho, jaká v daném místě povrchová impedance. Na povrchu kovových elementů platí

E^{I} + E^{S} = \frac{J}{γ}

( 6.1A.6 )

kde γ [S.m^-1] je elektrická vodivost elementů. Uvažujeme-li dokonalou elektrickou vodivost kovových elementů (elektrická vodivost se bude blížit nekonečnu), pravá strana (6.1A.6) se bude blížit nule, takže v limitě dostáváme

E^{I} + E^{S} = 0

( 6.1A.7 )

Intenzitu rozptýleného elektrického pole E^S v bodě, jehož pozice je dána polohovým vektorem r, lze vypočíst pomocí vektorového potenciálu A

E^{S} (r) = - j ω μ {A + \frac{1}{k^{2}} \nabla [\nabla \cdot A (r)]}

( 6.1A.8 )

Zdrojem vektorového potenciálu A jsou proudy J, indukované dopadající vlnou na kovových elementech kmitočtově selektivního povrchu. Příspěvek proudu v bodě r’ k potenciálu v bodě r je přitom popsán Greenovou funkcí G. Pro vektorový potenciál tak dostáváme vztah

A (r) = \iint_{z d r o j e} G (r | r^{'}) J (r^{'}) d S^{'}

( 6.1A.9 )

Pro případ volného prostoru má Greenova funkce G tvar

G = \frac{\exp (- j k | r - r^{'} |)}{4 π | r - r^{'} |}

( 6.1A.10 )

Vzájemnou kombinací vztahů (6.1A.9), (6.1A.8) a (6.1A.7) získáme integrální rovnici pro elektrické pole v prostorové oblasti:

- j ω μ {\iint_{z d r o j e} G (r | r^{'}) \cdot J (r^{'}) d S^{'} + \frac{1}{k^{2}} \nabla [\nabla \cdot \iint_{z d r o j e} G (r | r^{'}) \cdot J (r^{'}) d S^{'}]} = - E^{I}

( 6.1A.11 )

Rovnici (6.1A.11) budeme řešit v oblasti prostorových kmitočtů. Převod (6.1A.11) do spektrální oblasti vykonáme ve dvou krocích. Nejprve převedeme rovnici (6.1A.8) jejím rozepsáním do složkového tvaru a vyjádřením vektorového potenciálu pomocí Fourierovy řady. Tím dostáváme [19]

[\begin{matrix} E_{x}^{S} (α_{m}, β_{n}) \\ E_{z}^{S} (α_{m}, β_{n}) \end{matrix}] = - j ω μ [\begin{matrix} 1 - \frac{α_{m}^{2}}{k^{2}} & \frac{- α_{m} β_{n}}{k^{2}} \\ \frac{- α_{m} β_{n}}{k^{2}} & 1 - \frac{β_{n}^{2}}{k^{2}} \end{matrix}] [\begin{matrix} A_{x} (α_{m}, β_{n}) \\ A_{y} (α_{m}, β_{n}) \end{matrix}]

( 6.1A.12 )

V druhém kroku převedeme vztah do oblasti prostorových kmitočtů (6.1A.9) [19]

A (α_{m}, β_{n}) = G (α_{m}, β_{n}) \cdot J (α_{m}, β_{n})

( 6.1A.13 )

Výpočtem Fourierovy transformace funkce (6.1A.10) bychom obdrželi [19] Greenovu funkci ve spektrální oblasti

G (α_{m}, β_{n}) = \frac{- j}{2 \sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}}

( 6.1A.14 )

kde z odmocniny se uvažuje jen řešení se zápornou imaginární částí.

Vzájemnou kombinací (6.1A.13), (6.1A.14) a (6.1A.12) dostaneme výsledný vztah pro elektrické pole ve spektrální oblasti

- \frac{1}{2 ω ε} \sum_{m, n} [\begin{matrix} \frac{k^{2} - α_{m}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \\ \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{k^{2} - β_{n}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \end{matrix}] [\begin{matrix} J_{x} (α_{m}, β_{n}) \\ J_{y} (α_{m}, β_{n}) \end{matrix}] \exp [j (α_{m} x + β_{n} y)] = - [\begin{matrix} E_{x}^{I} (x, y) \\ E_{y}^{I} (x, y) \end{matrix}]

( 6.1A.15 )

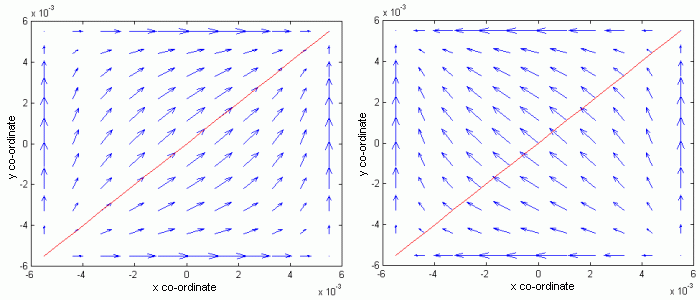
Řešení problému

Při řešení problému nejprve v rovnici (6.1A.15) aproximujeme neznámé rozložení proudové hustoty pomocí vhodně zvolených bázových funkcí a v tuto chvíli neznámých aproximačních koeficientů. Takovou formální aproximaci dosadíme do řešeného vztahu (6.1A.15). Jelikož aproximace řešení nesplňuje výchozí vztah zcela přesně, musíme tuto skutečnost respektovat přičtením zbytkové funkce (rezidua). Čím menších hodnot zbytková funkce nabývá, tím přesnější je nalezená aproximace. K minimalizaci rezidua přitom využijeme Galerkinovu metodu (reziduum postupně násobíme tolika bázovými funkcemi, kolik je neznámých aproximačních koeficientů; tak dostaneme soustavu N lineárních algebraických rovnic pro N neznámých aproximačních koeficientů).

Při volbě bázových funkcí existují v zásadě dva přístupy. První z nich používá bázové funkce, které nabývají nenulových hodnot na celé analyzované oblasti. Tyto funkce jsou voleny tak, aby fyzikálně odpovídaly stojatým vlnám proudu na elementu.

Druhý přístup dělí analyzovanou oblast na menší podoblasti, na nichž je proud aproximován pomocí bázových funkcí, jejichž funkční hodnota je nenulová jen na dané podoblasti. Výhoda tohoto přístupu spočívá v tom, že lze snadno analyzovat kmitočtově selektivní povrchy s libovolně tvarovanými elementy.

V našem článku se budeme zabývat pouze první skupinou bázových funkcí. Konkrétně za bázové funkce zvolíme harmonické funkce (první přístup, vrstva B) a harmonické funkce v kombinaci s Čebyševovými polynomy (druhý přístup, vrstva B).

Podrobnější popis využití výše uvedených bázových funkcí při řešení rovnice (6.1A.15) uvádíme ve vrstvě B. Zde, na základní úrovni učebnice, se seznámíme jen s dosaženými výsledky.

Harmonické bázové funkce

Uvažujme kmitočtově selektivní povrch, sestávající z pravoúhlých dokonale vodivých elementů o rozměrech a’ a b’. Aproximujeme-li rozložení proudu na elementu pomocí harmonických bázových funkcí, dostáváme pro vid (1, 1) pro rovnoběžnou polarizaci rozložení proudu, vykreslené na obr. 6.1A.3a, a pro polarizaci kolmou rozložení z obr. 6.1A.3b.

Obr. 6.1A.3

Směrové pole proudové hustoty vidu (1,1)
a) pro rovnoběžnou polarizaci (vlevo)
b) pro kolmou polarizaci
Rozměry buňky jsou a=b=12mm, rozměry kovového elementu jsou a' = b' = 12mm; f = 10GHz, ϑ = 1°, φ = 45°, d = 1.5mm, ε_r = 3.7. Velikost okrajových proudů byla uměle zmenšena oproti skutečnosti. Poloha roviny dopadu je vyznačena červeně.

Harmonické funkce v kombinaci s Čebyševovými polynomy

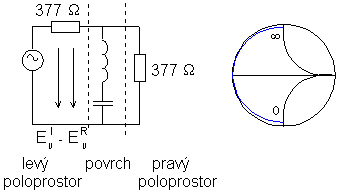
Obr. 6.1A.4

Náhradní obvodové schéma selektivního povrchu v kmitočtové oblasti; povrch sestává z kovových elementů (vlevo); ϑ = φ = 0. Činitel směrovosti ve Smithově diagramu (vpravo).

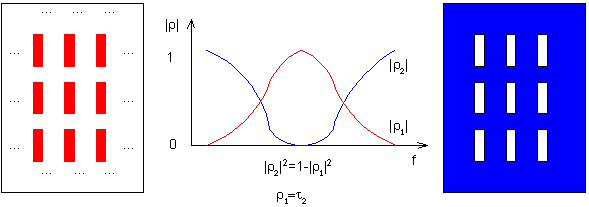
Rozdíl oproti ryze harmonickým bázovým funkcím spočívá v tom, že namísto funkce kosinus použijeme Čebyševův polynom, který na hranách elementu dosahuje nekonečných hodnot. Tak je zajištěno věrné modelování velkých proudů tekoucích po hranách.

Chování kmitočtově selektivního povrchu s kovovými elementy lze popsat také pomocí jeho ekvivalentního obvodu, v němž indukčnost elementů spolu s kapacitou mezi konci elementů tvoří sériový rezonanční obvod (obr. 6.1A.4). Činitele odrazu ρ, který je vykreslen v obr. 6.1A.4, počítáme podle vztahu

P^{T} = P^{I} [1 - {| ρ |}^{2}]

( 6.1A.16 )

kde P^I je výkon dopadajícího vlnění a P^T značí výkon vlnění, které povrchem prošlo do pravého poloprostoru. Odporem o hodnotě 377 Ω modelujeme volný prostor před povrchem (vlevo) a za povrchem (vpravo).

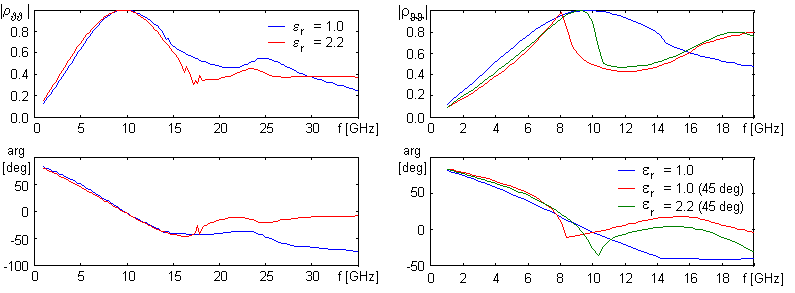
Obr. 6.1A.5

Povrch s obdélníkovými elementy, laděno pro 10 GHz, rovnoběžná polarizace.
a) kolmý dopad ϑ = 0°, φ = 90°
b) nekolmý dopad ϑ = 45°, φ = 90°

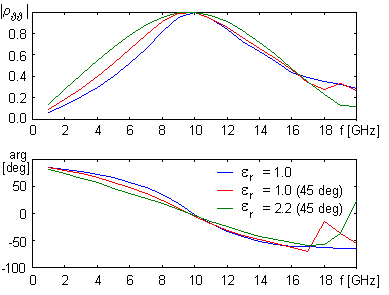
Chování činitele odrazu povrchu pro rovnoběžnou polarizaci je ukázáno v obr. 6.1A.5. Zajímavý je přitom případ bez dielektrika (b = 21 mm, a = 7.5 mm, b’ = 19.75 mm, a’ = 1.5 mm), kdy okolo 14.3 GHz dochází ke zlomu ve strmosti křivky činitele odrazu; to je způsobeno vybuzením prvního parazitního vidu (tzv. grating lobe).

Přidáním dielektrika a modifikací rozměrů (b = 17 mm, a = 7.5 mm, b’ = 15.75 mm, a’ = 1.5 mm, tloušťka substrátu d = 1.57 mm) nastane mírný pokles selektivity, ale zvětší se stabilita naladění povrchu pro nekolmý dopad (viz obr. 6.1A.5b). Dalšího zvětšení stability činitele odrazu na úhel dopadu by bylo možné dosáhnout přidáním horní dielektrické vrstvy. Díky přítomnosti dielektrika je rozměr buňky menší a parazitní vid se tedy budí na vyšším kmitočtu (17.6 GHz). V obr. 6.1A.5b však není vliv tohoto vidu příliš patrný.

Jak pro kolmý tak pro nekolmý dochází na vyšších kmitočtech ke vzniku parazitních rezonancí. Na kmitočtech vyšších než je kmitočet vzniku prvního parazitního vidu už vynesený činitel odrazu nevystihuje celkovou intenzitu odražené vlny, ale pouze intenzitu základního vidu (0,0).

Při buzení povrchu kolmou polarizací (na rozdíl od rovnoběžné polarizace) je činitel odrazu téměř nezávislý na úhlu dopadu (viz obr. 6.1A.6). Pro případ bez dielektrika uvažujeme rozměry b = 21 mm, a = 7.5 mm, b’ = 19.75 mm, a’ = 1.5 mm, pro případ s dielektrikem uvažujeme b = 17 mm, a = 7.5 mm, b’ = 15.75 mm, a’ = 1.5 mm a tloušťku substrátu d = 1.57 mm.

Obr. 6.1A.6

Povrch s obdélníkovými elementy, laděno na 10GHz, nekolmý dopad ϑ = 45°, φ = 0°, kolmá polarizace.

Štěrbinové elementy

Na rozdíl od povrchů s kovovými elementy vykazují kmitočtově selektivní povrchy se štěrbinami opačnou závislost činitele odrazu, tj. mají charakter pásmové zádrže. Pro případ bez dielektrika a pro případ s jednou metalickou vrstvou jsou tyto povrchy přesným komplementem povrchů s kovovými elementy.

povrch 1

povrch 2

Obr. 6.1A.7

Komplementární chování povrchů se štěrbinami a kovovými prvky. Činitel odrazu povrchu s kovovými prvky (1) je roven činiteli prostupu povrchu se štěrbinami (2).

Na tomto místě by bylo možné uvést duální odvození rovnice pro magnetickou intenzitu na apertuře povrchu se štěrbinami ve spektrální oblasti. Pokud se omezíme na případ bez dielektrika s jednou metalickou vrstvu, stačí uplatnit princip duality a rovnici pro magnetickou intenzitu získat z (6.1A.15) záměnou E ↔ H, ε ↔ μ, J ↔ J_M

- \frac{1}{2 ω μ} \sum_{m, n} [\begin{matrix} \frac{k^{2} - α_{m}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \\ \frac{- α_{m} β_{n}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} & \frac{k^{2} - β_{n}^{2}}{\sqrt{k^{2} - α_{m}^{2} - β_{n}^{2}}} \end{matrix}] [\begin{matrix} 2 J_{x}^{M +} (α_{m}, β_{n}) \\ 2 J_{y}^{M +} (α_{m}, β_{n}) \end{matrix}] \exp [j (α_{m} x + β_{n} y)] = - [\begin{matrix} 2 H_{x}^{I} (x, y) \\ 2 H_{y}^{I} (x, y) \end{matrix}]

( 6.1A.17 )

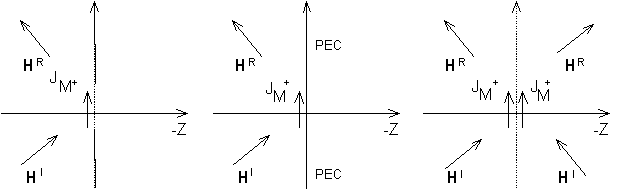
Při porovnání (6.1A.17) s rovnicí (6.1A.15) však čtenář zjistí nesrovnalost týkající se přítomnosti dvojky u hustoty magnetického proudu a budící magnetické intenzity. Kromě principu duality jsme totiž museli uvážit následující skutečnost.

Pole vyzařované elektrickými proudy u povrchu s kovovými prvky (angl. “scattered field”) není těmito prvky rozptylováno. Zatímco magnetické proudy ve štěrbinách produkují pole, které je elektricky vodivou plochou rozptylováno [19]. Aby se zahrnul i vliv okolní elektrické plochy, je nutné provést následující postup:

Nejprve pouze nahradíme originální proudy elektrické proudem magnetickým (tekoucím na ploše odpovídající štěrbině). Hustotu magnetického proudu lze přitom spočítat aplikací vztahu J_M⁺ = z × E_ap, kde E_ap je intenzita elektrického pole v apertuře (zde je nutné poznamenat, že podobně jako u proudu elektrického teče u i reálně tlustého magnetického vodiče proud pouze na jedné straně štěrbiny, a to na straně levé).
Nyní budeme předpokládat, že do štěrbiny umístíme ideální elektrický vodič, a vyrobíme tím tak nekonečně rozlehlou zemní plochu. Na tomto místě je nutné říci, že situace se tím nijak nezmění. Čtenář bude mít asi pocit, že dojde “ke zkratu” elektrického pole, které je generováno plošným magnetickým proudem (podle pravidla levé ruky). Není to však pravda, neboť na rozhraní dvou prostředí, tj. vzduchu a kovu platí mezi tečnými elektrickými intenzitami vztah $E_{t}^{k o v} - E_{t}^{v z d u c h} = J_{M}^{+} \times (- z)$ . Intenzita v kovu $E_{t}^{k o v} = 0$ je přitom nulová.
V posledním kroku se pouze aplikuje princip zrcadlení, čímž se převede problém v prostředním obrázku na problém ve volném prostoru (obr. 6.1A.8 vpravo).

původní problém po zavedení magnetického proudu

rozprostření zemní plochy a uvažování pouze levé poloroviny

aplikace principu zrcadlení

Obr. 6.1A.8

Vysvětlení principu ekvivalence

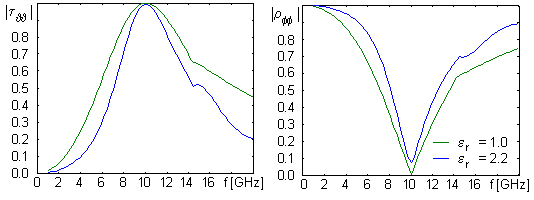
Podobně jako v případě kovových elementů je zde možné duálně formulovat činitel prostupu τ. Definice zde však nebude provedena, neboť by byla analogická s definicí, která byla provedena u činitele odrazu.

V obr. 6.1A.9 uvádíme příklad na kolmý dopad vlny na kmitočtově selektivní povrch se štěrbinami pro povrch ve vakuu (b = 21 mm, a = 7.5 mm, b’ = 19.75 mm, a’ = 1.5 mm) a pro povrch na dielektrickém substrátu (b = 14 mm, a = 7.5 mm, b’ = 13.25 mm, a’ = 1.5 mm a tloušťku substrátu d = 1.57 mm). Je zde vidět, že selektivita křivky činitele prostupu je v přítomnosti dielektrika lepší než pro případ ε_r = 1 (na rozdíl od povrchu s kovovými elementy, kde tomu bylo naopak). Dále platí, že vliv dielektrika je jiný než u povrchu s kovovými elementy, takže štěrbiny mají jiné rozměry než tomu bylo u povrchu s kovovými obdélníkovými elementy s dielektrikem. Přítomnost dielektrika je také zodpovědná za nenulovou hodnotu činitele odrazu na rezonančním kmitočtu. Stejně jako v předchozích případech, i zde se vyskytují parazitní vidy.

Závěr

Technika pro analýzu kmitočtově selektivní povrchů, popsaná v této kapitole, nezahrnuje vliv dielektrika. Uvedené příklady však tento vliv postihují, jak je popsáno v [17]. Jiný popis vlivu dielektrika lze nalézt v [19].

Reálné aplikace využívají několik selektivních povrchů řazených za sebou. Pak totiž dojde k podstatnému zlepšení selektivity. Návrh vícevrstvých povrchů však není jednoduchý.

Kmitočtově selektivní povrchy lze také omezeně modelovat v komerčních programech, založených na metodě konečných prvků (HFSS) nebo na metodě momentů (IE3D). V obou případech se díky periodicitě analyzuje pouze jedna buňka.

Při návrhu kmitočtově selektivních povrchů je bezpodmínečně nutná znalost jejich fyzikálního chování a znalost omezení, které tyto povrchy mají. Bez takové znalosti je návrh povrchů jenom hra s čísly.

prostup

odraz

Obr. 6.1A.9

Povrch s obdélníkovými štěrbinami, laděno na 10GHz, kolmý dopad, ϑ = 0° φ = 90°, kolmá polarizace