6.1 Analýza kmitočtově selektivních povrchůPodrobnější popisV této vrstvě učebnice se budeme zabývat detailním pohledem na bázové funkce, které se při analýze kmitočtově selektivních povrchů používají při numerickém hledání rozložení proudu na elementu. Vrstva tedy výjimečně nemá charakter souvislého textu, ale soustředí se jen na řešení dílčího, náročnějšího problému. Ve vrstvě A jsme dospěli pro kmitočtově selektivní povrch, sestávající z kovových elementů, ke vztahu pro elektrické pole v oblasti prostorových spekter
Ve výše uvedeném vztahu značí ω úhlový kmitočet vlny, ε je permitivita okolí kmitočtově selektivního povrchu, αm a βn jsou prostorové kmitočty, k značí vlnové číslo ve volném prostoru (ve vakuu), Jx a Jy jsou složky vektoru proudové hustoty na elementu a konečně, ExIa EyI značí složky vektoru elektrické intenzity dopadající vlny. Při řešení problému nejprve v řešené rovnici (6.1B.1) aproximujeme neznámé rozložení proudové hustoty pomocí vhodně zvolených bázových funkcí a v tuto chvíli neznámých aproximačních koeficientů. Takovou formální aproximaci dosadíme do řešeného vztahu (6.1B.1). Jelikož aproximace řešení nesplňuje výchozívztah zcela přesně, musíme tuto skutečnost respektovat přičtením zbytkové funkce (rezidua). Čím menších hodnot zbytková funkce nabývá, tím přesnější je nalezená aproximace. K minimalizaci rezidua přitom využijeme Galerkinovu metodu (reziduum postupně násobíme tolika bázovými funkcemi, kolik je neznámých aproximačních koeficientů; tak dostaneme soustavu N lineárních algebraických rovnic pro N neznámých aproximačních koeficientů). Při volbě bázových funkcí existují v zásadě dva přístupy. První z nich používá bázové funkce, které nabývají nenulových hodnot na celé analyzované oblasti. Tyto funkce jsou voleny tak, aby fyzikálně odpovídaly stojatým vlnám proudu na elementu. Druhý přístup dělí analyzovanou oblast na menší podoblasti, na nichž je proud aproximován pomocí bázových funkcí, jejichž funkční hodnota je nenulová jen na dané podoblasti. Výhoda tohoto přístupu spočívá v tom, že lze snadno analyzovat kmitočtově selektivní povrchy s libovolně tvarovanými elementy. Harmonické bázové funkceUvažujme kmitočtově selektivní povrch, sestávající z pravoúhlých dokonale vodivých elementů o rozměrech a’ a b’. Složky proudové hustoty J lze pak aproximovat následovně [17]
kde
Zde ΨpqTE a ΨpqTM představují dvě rozdílné funkce pro rovnoběžnou polarizaci a pro polarizaci kolmou. Tyto funkce se liší ve dvou ohledech:
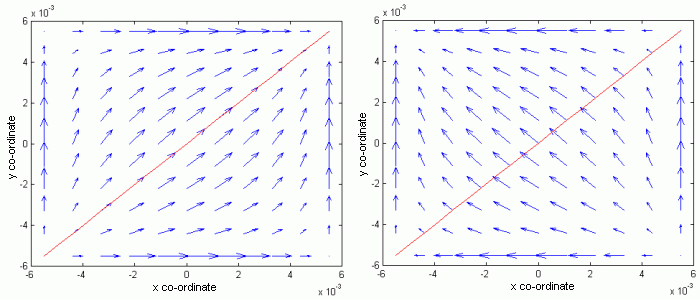
Aby měl čtenář lepší povědomí o tom, jaký je vizuální rozdíl mezi proudy buzenými elektrickou intenzitou dopadající vlny, která je rovnoběžná resp. kolmá v rovině dopadu, jsou v obr. 6.1B.1 vykreslena směrová pole proudové hustoty pro vid (1,1) pro rovnoběžnou a kolmou polarizaci.
Harmonické funkce v kombinaci s Čebyševovými polynomy
Rozdíl oproti předchozímu je v tom, že namísto funkce kosinus nyní vystupuje Čebyševův polynom. Funkce je volena záměrně tak, aby na hranách dosahovala nekonečných hodnot. Tak je zajištěno věrné chování velkých proudů tekoucích po hranách. Nyní přistoupíme k řešení rovnice (6.1B.1) Galerkinovou metodou: rovnici (6.1B.1) postupně násobíme bázovými funkcemi a součin integrujeme přes plochu buňky. Pro ryze harmonické bázové funkce dostaneme soustavu
Po vyřešení této soustavy následuje výpočet elektrické intenzity ES ve spektrální oblasti. Intenzita ES je přítomna na levé straně v rovnici (6.1B.1)
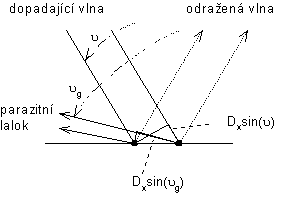
Při výpočtu intenzity odražené vlny ES = ER budeme přitom uvažovat jen základní harmonickou složku na kmitočtu α0, β0. Pokud je perioda a malá (zpravidla ne více jak polovina délky vlny) a kmitočet se pohybuje v okolí první rezonance povrchu, pak ve vzdálené oblasti od povrchu existuje pouze uniformní pole odražené vlny. Pokud podmínka není splněna, může dojít k vybuzení tzv. parazitních vidů (vyšší prostorové kmitočty nejsou v blízké zóně odfiltrovány a jim odpovídající vlny se šíří dále). Nyní si vysvětleme, co parazitní vidy šíření fyzikálně znamenají. K ilustraci slouží obr. 6.1B.2. Zachycuje anténní řadu (dvouprvkovou), na kterou dopadá pod obecným úhlem ϑ rovinná vlna. Při dopadu dojde k odrazu podle pravidel geometrické optiky. Část energie se však může šířit i ve směru parazitního laloku (angl. grating lobe).
Vznik parazitního laloku je podmíněn dosažením fázového zpoždění rovného násobku 2π paprskem 1 na tučně vyznačené trajektorii. Matematicky zapsáno:
Směr, ve kterém se objeví parazitní lalok, přitom závisí pouze na kmitočtu dopadající vlny a rozestupu anténních elementů. Nejnižší kmitočet, při kterém se pro daný úhel dopadu vybudí parazitní lalok, nastane pro případ ϑg = 90°:
Například pro rozestup prvků a = 21 mm a kolmém dopadu budící (dopadající) vlny se vybudí první parazitní lalok na kmitočtu
| ||||||||||||||||||||||||||||||||||||||||||||||||