Multimediální učebnice

Kapitola 7: Radiooptika

Úvod

Pod pojmem elektrický signál máme většinou na mysli v čase proměnné napětí U(t), proud I(t) nebo intenzitu elektrického pole E(t). V časové závislosti těchto veličin je zakódovaná nějaká informace.

Každý elektrický signál je možné složit z konečného či nekonečného počtu harmonických napětí (proudů, intenzit) s různými kmitočty, amplitudami a počátečními fázemi. Amplitudy a fáze těchto spektrálních složek udává tzv. spektrální funkce S(ω). Signál může být tedy popsán vztahem

U (t) = \frac{1}{2 π} \int_{- \infty}^{+ \infty} S (ω) e^{j ω t} d ω

( 7.1 )

V tomto vztahu značí ω úhlový kmitočet a t je čas.

Říkáme, že signál je dán součtem svých spektrálních složek nebo že je dán zpětnou Fourierovou transformací své spektrální funkce (dle (7.1)). Protože prosté harmonické kmitání je základním stavebním kamenem signálu, považujeme toto kmitání za elementární signál, i když samo žádnou informaci nenese. Elementární signál je určen amplitudou, fází a (časovým) kmitočtem f, resp. časovou periodou T = 1/f.

Elektromagnetické vlnění může obsahovat informace v časové závislosti intenzity elektrického pole E(t). Protože však toto vlnění existuje na rozdíl od napětí či proudu také v prostoru, může být informace rovněž obsažena v prostorovém rozložení intenzity. Potom mluvíme o optickém signálu. Prostorový signál je proti signálu elektrickému bohatší, protože je funkcí dvou proměnných (x, y). Je vždy nesený elektromagnetickou vlnou, konkrétně rozložením amplitudy intenzity pole v rovině kolmé na směr šíření vlny.

Analogicky k elementárnímu elektrickému signálu lze zavést i elementární prostorový signál. Zavedeme-li na rovině kolmé ke směru šíření vlny (která signál nese) souřadný systém x,y, pak elementárním optickým signálem je prostá harmonická změna amplitudy (nikoli okamžité hodnoty) intenzity pole ve směru některé osy (např. x). Ve směru druhé osy je amplituda intenzity konstantní (na y nezávislá). Kdyby takové vlnění (v oblasti viditelného světla) dopadalo na projekční plátno, viděli bychom osnovu tmavých a světlých pruhů s neostrými přechody (nejtmavější pruhy odpovídají minimu harmonické funkce, nejsvětlejší pruhy odpovídají maximu). Vzdálenost dvou sousedních pruhů se nazývá prostorová perioda T_x. Převrácená hodnota prostorové periody se nazývá prostorová frekvence f_x. Matematické vyjádření elementárního optického signálu např. pro směr osy x lze zapsat následovně:

E (x) = E_{m x} [1 + \sin (2 π f_{x} x)] = E_{m x} [1 + \sin (ω_{x} x)]

( 7.2 )

Analogicky pro směr y:

E (y) = E_{m y} [1 + \sin (2 π f_{y} x)] = E_{m y} [1 + \sin (ω_{y} x)]

( 7.3 )

Složením těchto elementárních prostorových signálů získáme prostorový signál dvojrozměrný:

E (x, y) = E_{m} [1 + \sin (ω_{x} x + ω_{y} y)]

( 7.4 )

Pro optické signály lze použít symbolické metody zápisu. Potom dostáváme:

E (x, y) = E_{m} [1 + \exp (j ω_{x} x) + \exp (j ω_{y} y)]

( 7.5 )

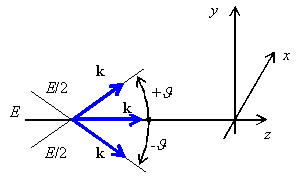
Obr. 7.1

Elementární optický signál je tvořen složením tří uniformních rovinných vln

Analogicky v časové oblasti. Každý prostorový signál E(x, y) lze složit z elementárních prostorových signálů s různými prostorovými kmitočty, s různými amplitudami a různými počátečními fázemi. Fourierova transformace odpovídající (7.1) je ovšem dvourozměrná.

Elementární prostorový signál je neuniformní rovinou vlnou. S těmito vlnami je obtížné počítat, a proto se používá rozkladu neuniformní vlny na tři rovinné vlny uniformní. V obr. 7.1 jsou modrými šipkami vyznačeny směry šíření tří paraxiálních vln s amplitudami E/2, E a E/2, které se šíří třemi směry symetricky podél osy z. Šipky s označením k jsou jejich vlnové vektory. Vypočteme rozložení výsledné intenzity pole v rovině x,y ve směru rovnoběžném s osou y . K tomu cíli nalezneme nejprve průměty vlnových vektorů do směru y:

k_{0 y} = 0

k_{1 y} = k \sin (+ ϑ)

k_{2 y} = k \sin (- ϑ)

( 7.6 )

Hledaná intenzita je součtem intenzit tří rovinných vln s vlnovými čísly k_1y, k_oy, k_2y, šířících se ve směru y:

\begin{array}{l} E (y) = \frac{E_{m}}{2} \exp (j k_{1 y} y) + E_{m} + \frac{E_{m}}{2} \exp (j k_{2 y} y) = \\ = E_{m} [\frac{\exp (+ j k \sin ϑ y)}{2} + 1 + \frac{\exp (- j k \sin ϑ y)}{2}] = \\ = E_{m} [1 + \cos (k \sin ϑ y)] \end{array}

( 7.7 )

Získali jsme kosinusové rozložení amplitudy Ey, tedy elementární optický signál s úhlovou prostorovou frekvencí ω_y= k.sin ϑ.

Teď jsme schopni obecný prostorový signál rozložit pomocí Fourierovy transformace na elementární optické signály a každý elementární signál můžeme dále rozložit na trojici obyčejných uniformních vln.

Právě popsané principy tvoří v podstatě základ radiooptiky – na rádiových kmitočtech pracujeme s prostorovým rozložením signálu, jako je tomu v optice. Pokud si uvědomíme, že prostorový signál je elektromagnetické vlnění (ovšem s mnohem vyšším kmitočtem, než jsme zvyklí), není důvod, proč bychom tak nemohli činit.

V čl. 7.1 popisujeme tzv. Gaussův svazek – úzký svazek koherentního záření, kterým může být např. laserový svazek základního vidu TEM₀₀, jenž vystupuje ze zdroje jako rovnoběžný (tj. s vlnoplochou, která je rovinná a kolmá na směr šíření). Svazek paprsků není záměrně modulovaný, ale rozložení intenzity pole v příčném průřezu svazku není z podstaty konstantní. U zmíněného vidu je intenzita největší na ose svazku a zmenšuje se k okraji podle Gaussovy funkce. Gaussův svazek necháváme procházet soustavou prostorových vrstev a čoček a sledujeme, jak se mění jeho parametry. Úloha je typická zejména pro optické aplikace, ale setkáme se s ní i na nízkých (rádiových) kmitočtech.

Čl. 7.2 se zabývá popisem průchodu Gaussova svazku různými prostorovými prvky (čočky, vrstvy prostředí, atd.), a to pomocí maticového zápisu. Gaussův svazek je popsán vektorem svých parametrů, optické prvky jsou popsány maticemi. Vynásobením vektoru, obsahujícího parametry Gaussova svazku na vstupu prvku, s maticí prvku, dostáváme vektor, obsahující parametry Gaussova svazku na výstupu tohoto prvku.