Multimediální učebnice

7.2 Průchod Gaussova svazku optickými prvky

Základní teorie

V tomto článku budeme studovat, jak ovlivní parametry Gaussova svazku průchod svazku různými optickými prvky. Pokud necháme Gaussův svazek šířit kruhově symetrickou soustavou tvořenou řadou optických prvků, zůstává svazek stále svazkem gaussovským a pouze se mění jeho parametry. Změnu parametrů Gaussova svazku můžeme jednoduše stanovit pomocí tzv. maticové optiky.

Parametry Gaussova svazku můžeme sledovat v závislosti na poloze bodu pozorování (souřadnice na optické ose) a na úhlu, který svírá průvodič bodu pozorování s optickou osou. V paraxiální aproximaci jsou poloha a úhel vzájemně svázány dvěma algebraickými rovnicemi. Optická soustava je tudíž popsána maticí o rozměru 2 × 2. Tato matice se nazývá maticí svazku. Obecně lze tedy napsat:

\begin{matrix} y_{2} = A y_{1} + B Θ_{1} \\ Θ_{2} = C y_{1} + D Θ_{1} \end{matrix} [\begin{matrix} y_{2} \\ Θ_{2} \end{matrix}] = [\begin{matrix} A & B \\ C & D \end{matrix}] [\begin{matrix} y_{1} \\ Θ_{1} \end{matrix}]

( 7.2A.1 )

kde y₁ je poloha vstupu optického prvku, y₂ je poloha jeho výstupu, θ₁ je úhel na vstupu optického prvku a θ₂ je úhel na jeho výstupu (vzhledem k optické ose).

Zákon ABCD

Označme symbolem q₁ parametry Gaussova svazku ve vstupní rovině optického prvku a symbolem q₂ parametry Gaussova svazku ve výstupní rovině optického prvku. Samotný optický prvek nechť je popsán maticí [A, B; C, D]. Lze ukázat, že všechny právě uvedené veličiny jsou svázány vztahem

q_{2} = \frac{A q_{1} + B}{C q_{1} + D}

( 7.2A.2 )

Protože parametry q určují pološířku Gaussova svazku W a jeho poloměr křivosti R, popisuje jednoduchý zákon (7.2A.2), který nazýváme zákonem ABCD, transformaci Gaussova svazku libovolnou paraxiální optickou soustavou.

Přenosové matice jednoduchých optických prvků

V tomto odstavci si uvedeme matice nejčastěji používaných optických prvků.

Šíření vakuem

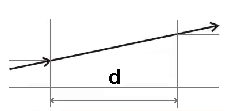Obr. 7.2A.1

Šíření vakuem o délce d

Za nejjednodušší optickou soustavu můžeme považovat úsek volného prostoru (vyplněného vakuem) o délce d. Protože ve vakuu se vlny šíří podél paprsků, změní se souřadnice paprsku, který prošel vzdálenost d, podle rovnice y₂ = y₁ + θ₁d a θ₂ = θ₁.
Přenosová matice M se tedy rovná

M = [\begin{matrix} 1 & d \\ 0 & 1 \end{matrix}]

( 7.2A.3 )

Lom na rovinném rozhraní

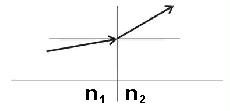Obr. 7.2A.2

Lom na rovinném rozhraní dvou prostředí s různými indexy lomu

Na rovinném rozhraní mezi dvěma prostředími s indexy lomu n₁ a n₂ se úhly paprsku mění podle Snellova zákona

n_{1} \sin (Θ_{1}) = n_{2} \sin (Θ_{2})

( 7.2A.4 )

V paraxiální aproximaci platí n₁θ₁ ≈ n₂θ₂, a proto se poloha paprsku nemění, tj. y₂ = y₁. Přenosová matice je tedy

M = [\begin{matrix} 1 & 0 \\ 0 & n_{1} / n_{2} \end{matrix}]

( 7.2A.5 )

Lom na sférickém rozhraní

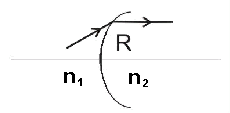vypuklé rozhraní: R>0
vyduté rozhraní: R<0

Obr. 7.2A.3

Lom na sférickém rozhraní dvou různých indexů lomu

Vztah mezi úhly θ₁ a θ₂ pro paraxiální paprsky lámající se na sférickém rozhraní mezi dvěma prostředími je dán vztahem

Θ_{2} \approx \frac{n_{1}}{n_{2}} Θ_{1} - \frac{n_{2} - n_{1}}{n_{2} R} y

( 7.2A.6 )

Vzdálenost paprsku od osy se nemění, tj. y₂ ≈ y₁. Pro tento optický prvek lze tedy zapsat přenosovou matici ve tvaru:

M = [\begin{matrix} 1 & 0 \\ - \frac{(n_{2} - n_{1})}{n_{2} R} & \frac{n_{1}}{n_{2}} \end{matrix}]

( 7.2A.7 )

Průchod tenkou čočkou

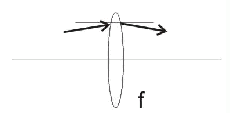vypuklá čočka: f>0
vydutá čočka: f<0

Obr. 7.2A.4

Průchod čočkou o ohniskové vzdálenosti f

Vztah mezi úhly θ₁ a θ₂ pro paraxiální paprsky, které procházejí tenkou čočkou s ohniskovou vzdáleností f, je:

Θ_{2} = Θ_{1} - \frac{y}{f}

( 7.2A.8 )

přičemž vzdálenost od osy se nemění. Pro přenosovou matici tedy platí vztah:

M = [\begin{matrix} 1 & 0 \\ - 1 / f & 1 \end{matrix}]

( 7.2A.9 )

Odraz od rovinného zrcadla

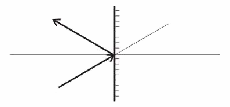Obr. 7.2A.5

Odraz od rovinného zrcadla

Při odrazu od rovinného zrcadla se poloha paprsku nemění (y₂ = y₁). Pro úhly platí θ₂ = θ₁. Z toho plyne, že přenosová matice paprsku bude jednotková

M = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}]

( 7.2A.10 )

Odraz od sférického zrcadla

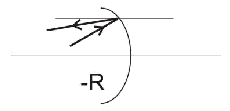vypuklé zrcadlo:
vyduté zrcadlo:

Obr. 7.2A.6

Odraz od sférického zrcadla

S využitím (7.2A.9) dostáváme pro zrcadlo přenosovou matici:

(- Θ_{2}) + Θ_{1} \approx \frac{2 y}{- R}

( 7.2A.11 )

M = [\begin{matrix} 1 & 0 \\ 2 / R & 1 \end{matrix}]

( 7.2A.12 )

Přenosové matice řady optických prvků

Obr. 7.2A.7

Řazení optických prvků

Řada optických prvků, jež jsou popsány maticemi M₁, M₂, …, M_N, je ekvivalentní jedinému optickému prvku s přenosovou maticí:

M = M_{1} \cdot M_{2} \cdot \dots \cdot M_{N}

( 7.2A.13 )

Všimněme si pořadí násobení matic. Matice prvku, do něhož vstupuje paprsek nejdříve, je umístěna napravo, takže jako první násobí sloupcovou matici popisující dopadající paprsek.

Podrobnější informace čtenář nalezne v [16].