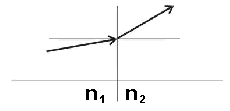7.2 Passage of Gaussian beam through optic elements

Basic theory

In this paragraph, influence of various optical elements to the parameters of passing Gaussian beam is studied. If Gaussian beam propagates through a circularly symmetric system, which consists of a sequence of optical elements, then the nature of a beam stays Gaussian, and only its parameter change. This change of parameters can be simply computed by matrix optics.

Parameters of Gaussian beam can be observed depending on the position of the observation point (a coordinate on the optical axis) and on the angle between the position vector of the observation point and the optical axis. In paraxial approximation, the position and the angle are mutually associated by two algebraic equations. The optical system is therefore described by the matrix of size 2 × 2. This matrix is called the matrix of beam. In general:

Here, y₁ is position of the input of an optical element, y₂ is position of the output, θ₁ is an angle at the input of the optical element, and θ₂ is an angle at the output (with respect to the optical axis).

ABCD law

Let us denote parameters of Gaussian beam at the input plane of the optical element as q₁, and parameters of Gaussian beam at the output plane of the optical element as q₂. The optical element is described by the matrix [A, B; C, D]. We can show that all the introduced quantities are related by the equation

Since parameters q determine the half-width of the Gaussian beam W and its curvature radius R, eqn. (7.2A.2), which is called ABCD law, describes the transform of the Gaussian beam by an arbitrary paraxial optical system.

Transmission matrices of simple optical elements

In this paragraph, matrices of the most frequently used optical elements are given.

Propagation in vacuum

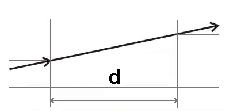Fig. 7.2A.1 Vacuum of the length d

A distance d in free space can be considered as the simplest optical element. Since wave propagates along beams, coordinates of the beam, which passes through the distance d, change according to the equation y₂= y₁ + θ₁d and θ₂ = θ₁. The transmission matrix M is therefore

Refraction on planar boundary

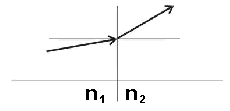Fig. 7.2A.2 Refraction on planar boundary of two media of different refraction index

On planar boundary of two media of refraction indexes n₁ and n₂, angles of the beam change according to the Snell law

In paraxial approximation, we have n₁θ₁ ≈ n₂θ₂, and therefore, position of the beam stays unchanged, i.e. y₂ = y₁. The transmission matrix M is therefore

Refraction on spherical boundary

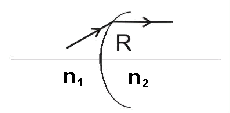convex boundary: R>0 concave boundary: R<0

Fig. 7.2A.3 Refraction on spherical boundary of two media of different refraction index

Relation between angles θ₁ and θ₂ for paraxial beams refracting on a spherical boundary of two media is given by

The distance of the beam from the axis stays unchanged, i.e. y₂ ≈ y₁. The transmission matrix M is therefore:

Passage through a thin lens

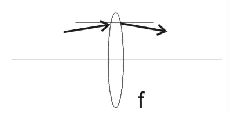convex lens: f>0 concave lens: f<0

Fig. 7.2A.4 Passage through a lens of focus distance f

Relation between angles θ₁ and θ₂ for paraxial beams, which pass through a thin lens of the focus distance f, is:

The distance form the axis stays unchanged. The transmission matrix M is therefore:

Reflection from planar mirror

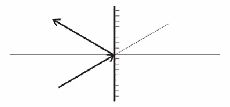Fig. 7.2A.5 Reflection from planar mirror

Reflecting beam from a planar mirror, the position of a beam stays unchanged (y₂ = y₁). For angles, we get θ₂ = θ₁. Hence, the transmission matrix is unitary

Reflection from spherical mirror

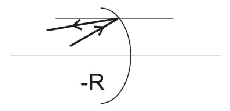convex mirror: concave mirror:

Fig. 7.2A.6 Reflection from spherical mirror

Exploiting (7.2A.9), we obtain:

Transmission matrix of the sequence of optical elements

Fig. 7.2A.7 Sequencing optical elements

Sequence of optical elements, which are described by matrices M₁, M₂, ..., M_N, is equivalent to a single optical element of the transmission matrix:

Note the order of the matrix multiplication. The matrix of the element, which is entered by the beam first, appears on the right, and therefore, it multiplies the column vector of the incident beam first.

More information can be found in [16].