Multimediální učebnice

8.1 Model driftu a difuze

Základní teorie

1 Základní rovnice pro polovodiče

Modelování polovodičových prvků a součástek v praxi představuje problém transportu částic v makroskopickém měřítku. V takovém případě uvažujeme popis pohybu nosičů náboje (např. elektronu) mezi jednotlivými interakcemi s atomovou mřížkou polovodiče Newtonovými zákony a samotné interakce popisujeme statisticky nástroji kvantové fyziky. Takový systém je možné popsat Boltzmanovou kinetickou rovnicí, jejímž řešením je distribuční funkce nosičů náboje v objemu polovodiče. Takové řešení však vyžaduje náročný matematický aparát, proto byla zavedena řada zjednodušení, které redukují takový systém v jednoduchou soustavu parciálních diferenciálních rovnic (8.1A.1), které tvoří matematický popis polovodičů nazývaný model driftu a difůze. Tyto rovnice jsou také v některých publikacích nazývány jako Základní rovnice pro polovodiče a jejich forma vychází z Maxwellových rovnic, ze kterých se dají pomocí idealizujících předpokladů snadno odvodit.

\nabla \cdot (\nabla Ψ) = \frac{q}{ε} (n - p - C)

( 8.1A.1a )

\nabla \cdot (J_{n}) - q \frac{\partial n}{\partial t} = q R

( 8.1A.1b )

\nabla \cdot (J_{p}) + q \frac{\partial p}{\partial t} = - q R

( 8.1A.1c )

J_{n} = q n μ_{n} E + q D_{n} \nabla n

( 8.1A.1d )

J_{p} = q p μ_{p} E - q D_{p} \nabla p

( 8.1A.1e )

Rovnice (8.1A.1a) představuje Poissonovu rovnici pro elektrický potenciál Ψ, kde volná hustota náboje je rozepsána pomocí elementárního náboje q a koncentrace záporně nabitých elektronů n, koncentrace kladně nabitých děr p a koncentrace pevného náboje příměsí C. Symbol ε v této rovnici značí permitivitu použitého polovodiče. Hodnoty relativní permitivity pro nejběžnější materiály jsou uvedeny v tab. 8.1A.1.

Tab. 8.1A.1

Typické hodnoty relativní permitivity. [44].

Materiál	ε_r []
Si	11,7
SiO₂	3,9
Si₃N₄	7,2
GaAs	12,5
Ge	16,1

Rovnice kontinuity (8.1A.1b) a (8.1A.1c) vyjadřují to, že zřídlové oblasti proudové hustoty jsou plně kompenzovány časovou změnou volného náboje a společnou funkci R, která vyjadřuje četnost generace a rekombinace elektronů a děr. Dále J_n značí proudovou hustotu způsobenou elektrony, J_p proudovou hustotu způsobenou děrami a t je čas. Vyjádření četnosti R vyžaduje dobrou znalost fyzikálních mechanismů generace a rekombinace v polovodičových materiálech a je jedním z klíčových parametrů pro získání relevantních výsledku simulací polovodičových struktur.

U obou rovnic proudových hustot (8.1A.1d) a (8.1A.1e) první člen na pravé straně představuje složku proudové hustoty způsobenou Lorenzovou silou s uvážením vlivu pouze elektrického pole E (vliv magnetické indukce je zanedbána) a zavádí efektivní pohyblivost elektronů μ_n a děr μ_p, které jsou funkcí průměrné četnosti kolize nosičů, a jejich hodnota je zpravidla definována empirickými vztahy. Pohyblivost nosičů náboje je veličina, která má velký vliv na vlastnosti polovodičových součástek a proto je její správná formulace velmi důležitá. Druhý člen na pravé straně rovnic (8.1A.1d) a (8.1A.1e) představuje vliv difůze nosičů ve směru gradientu jejich koncentrace a zavádí Einsteinovy difúzní konstanty

D_{n} = μ_{n} \frac{k T}{q}

( 8.1A.2a )

D_{p} = μ_{p} \frac{k T}{q}

( 8.1A.2b )

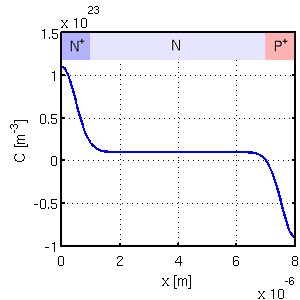
kde k je Boltzmanova konstanta a T je teplota.

2 Fyzikální parametry

Uvedené rovnice (8.1A.1) tvoří základní rovnice umožňující analýzu a simulaci většiny polovodičových prvků. Avšak mohou nastat případy, kdy nabývají na významu fyzikální jevy jež nejsou dostatečně v těmito rovnicemi podchyceny. Tak je tomu v případě tunelových proudů skrz velmi tenké vrstvy, které mají významný vliv na vlastnosti prvku. V praxi se ukázalo efektivnější aplikovat v těchto případech empirické korekce, než daný systém rovnic dále rozšiřovat.

Fyzikální parametry v těchto rovnicích definují geometrii prvku, druh polovodičového materiálu a technologii použitou při jeho výrobě. Jejich modelováním se budeme zabývat v následujících odstavcích.

Dotační profil

Distribuce příměsí v objemu polovodiče, mající za následek nevlastní vodivost typu N nebo P, určuje geometrii a funkci polovodičového prvku. Proto je to naprosto zásadní vstupní informace a tudíž je pochopitelné, že pro přesné výsledky simulací je zapotřebí věrné modelování používaných výrobních procesů, jako jsou iontová implantace, difůze, tepelná oxidace, epitaxní narůstání a jiné, které tuto distribuci (dotační profil) vytvářejí. Díky šíři tohoto tématu se omezíme jen na procesy iontové implantace a difůze atomů příměsi do objemu polovodičového substrátu. Výsledné profily těchto procesů jsou nejčastěji modelovány Gaussovou funkcí. Příklad dotačního profilu P-N diody je zobrazený na obr. 8.1A.1.

Obr. 8.1A.1

Příklad dotačního profilu P-N diody

Pohyblivost nosičů

Pohyb nosičů v polovodiči je narušen kolizemi s krystalovou mřížkou, příměsemi a defekty, tudíž dráha pohybu nosiče mezi dvěma body není přímka. Z důvodu snadnější představitelnosti tohoto jevu se zavedla právě veličina pohyblivosti, která se modeluje s ohledem na mechanismy, které ovlivňují kolize nosičů. Tyto mechanizmy mohou být způsobeny např.

atomovou mřížkou materiálu
ionizovanými nečistotami
kolizí nosič-nosič
neutrálními nečistotami
intenzitou elektrického pole

Často si vystačíme pouze s tabulkovou hodnotou $μ_{n, p}^{300}$ , udávanou pro daný materiál při teplotě 300K viz. tab. 8.1A.2.

Tab. 8.1A.2

Typické hodnoty pohyblivosti nosičů při 300K [44].

materiál	$μ_{n}^{300}$ [m²V^-1s^-1]	$μ_{p}^{300}$ [m²V^-1s^-1]
Si	0,14	0,04
GaAs	0,8	0,04
Ge	0,38	0,18

Generace a rekombinace nosičů

V předchozích odstavcích byla zmíněna funkce R, která popisuje četnost generace a rekombinace elektronů a děr. Dominantním mechanismem je tzv. Shockley-Read-Hall, která je vyjádřena následujícím vztahem.

R^{S R H} = \frac{n p - n_{i}^{2}}{τ_{p} (n + n_{i}) + τ_{n} (p + p_{i})}

( 8.1A.3 )

kde τ_n a τ_p jsou doby života nosičů a n_i je hodnota intrinsické koncentrace.

3 Analýza základních rovnic a okrajové podmínky

První sekci byl uveden soubor základních rovnic (8.1A.1). Je důležité zmínit, že ve vztazích proudových hustot (8.1A.1d) a (8.1A.1e) byly opomenuty složky proudu způsobené zúžením zakázaného pásma a teplotním gradientem, protože jsou vlivy těchto efektů považovány za zanedbatelné. Avšak je nutné si uvědomit, že vztahy pro proudy se tímto mohou stát nekorektní, pokud některý ze zmíněných efektů zásadně nabude na významu.

Použitím (8.1A.1a) a substitucí rovnic proudové hustoty (8.1A.1d) a (8.1A.1e) do rovnic kontinuity (8.1A.1b) a (8.1A.1c) dostáváme systém tří parciálních diferenciálních rovnic (8.1A.4) s proměnnými Ψ, n a p.

\nabla \cdot (\nabla ψ) - \frac{q}{ε} (n - p - C) = 0

( 8.1A.4a )

\nabla \cdot (D_{n} \nabla n - n μ_{n} \nabla ψ) - R = \frac{\partial n}{\partial t}

( 8.1A.4b )

\nabla \cdot (D_{p} \nabla p + p μ_{p} \nabla ψ) - R = \frac{\partial p}{\partial t}

( 8.1A.4c )

Pro matematickou analýzu potřebujeme znát počáteční odhad proměnných Ψ, n a p v doméně, ve které jsou tyto rovnice platné a okrajové podmínky. Tato ohraničená doména D je obecně trojrozměrná, tak jako prakticky všechny polovodičové struktury. Avšak v mnoha případech můžeme tuto doménu považovat za dvojrozměrnou, či dokonce za jednorozměrnou, čímž se analyzovaný problém zásadně zjednoduší.

Nechť ∂D značí dílčí hranice domény D. Tato může být z principu rozdělena na dvě části

\partial D = \partial D_{p} \cup \partial D_{a}

( 8.1A.5 )

kde ∂D_p značí ty části hranice, které představují skutečné, fyzické, hranice, jako jsou kontakty a rozhraní. Naopak ∂D_a značí umělé rozhraní, které zavádíme například za účelem vyčlenění dílčí struktury z rozměrného substrátu nebo oddělení sousedních prvků na jednom substrátu, tudíž nepředstavují fyzickou hranici.

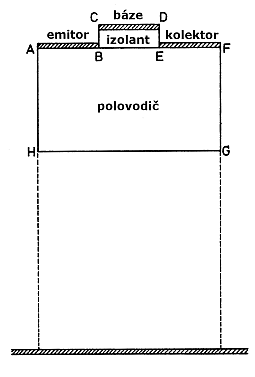
Obr. 8.1A.2

2D geometrie planárního tranzistoru MOSFET [44]

Zmíněné rozdělení hranic ilustrativně popíšeme na idealizované geometrii 2D planárního MOS tranzistoru, viz. obr. 8.1A.2. Celá doména je reprezentována mnohoúhelníkem A-B-C-D-E-F-G-H-A. Rovnice (8.1A.4) platí pouze v subdoméně A-B-E-F-G-H-A. Izolant, ohraničený body B-C-D-E-B, můžeme charakterizovat buď Laplaceovou rovnicí pro elektrostatický potenciál (8.1A.6) nebo předpokladem absence nosičů náboje (8.1A.7).

\nabla \cdot \nabla (Ψ) = 0

( 8.1A.6 )

n = p = C = 0

( 8.1A.7 )

Avšak použití těchto rovnic znemožňuje určení proudu procházející bází a vliv náboje izolační vrstvy oxidu.

Hranice A-B, E-F, C-D a B-E můžeme pokládat za fyzické hranice představující tři kontakty a jedno rozhraní mezi polovodičem a izolantem. Hranice A-H, B-C, D-E, F-G a G-H pokládáme za umělé hranice. Tyto sice v reálné struktuře neexistují, ale usnadňují simulaci tím, že strukturu separují od okolního prostředí.

Fyzické hranice mohou být rozděleny do tří kategorii.

\partial D_{P} = \partial D_{O} \cup \partial D_{S} \cup \partial D_{I}

( 8.1A.8 )

kde ∂D_O značí ohmický kontakt, ∂D_S značí Schottkyho kontakt a ∂D_I značí rozhraní s izolantem.

Přehled okrajových podmínek pro všechny tři závislé proměnné soustavy (8.1A.4) je uveden v následující tab. 8.1A.3, kde n značí normálový vektor kolmý na ∂D a u_n,p značí rychlosti tepelné rekombinace.

Tab. 8.1A.3

Okrajové podmínky typických rozhraní polovodičových struktur.

	ohmický kontakt	Shottkyho kontakt	polovodič - izolant	umělé rozhraní
elektrický potenciál	$ψ_{b} = \frac{k T}{q} a r \sinh (\frac{C}{2 n_{i}})$	$ψ_{b} = \frac{k T}{q} a r \sinh (\frac{C}{2 n_{i}})$	$\frac{\partial ψ}{\partial n} = 0$	$\frac{\partial ψ}{\partial n} = 0$
koncentrace elektronů	$n = \frac{\sqrt[]{C^{2} + 4 n_{i}^{2}} + C}{2}$	$J_{n} n = - q u_{n} (n - \frac{\sqrt{C^{2} + 4 n_{i}^{2}} + C}{2})$	$J_{n} n = 0$	$\frac{\partial n}{\partial n} = 0$
koncentrace děr	$p = \frac{\sqrt[]{C^{2} + 4 n_{i}^{2}} - C}{2}$	$J_{p} n = - q u_{p} (p - \frac{\sqrt{C^{2} + 4 n_{i}^{2}} - C}{2})$	$J_{p} n = 0$	$\frac{\partial p}{\partial n} = 0$