9.2 Některé pasivní obvody

Základní teorie

Odbočnice

Určení	k odebrání části výkonu, k rozlišení postupující a odražené vlny
Počet bran	3
Název modelu v programu WinMIDE	odboc

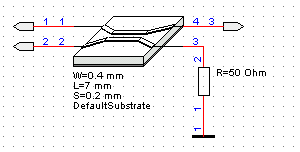Obr. 9.2A.18

Schéma odbočnice (kopie ze schematického editoru WinMIDE)

Uvedená odbočnice je založena na vlastnostech vázaného vedení. Pracuje na principu elektromagnetické vezby mezi dvěma vedeními. Maximum přenosu z brány 1 do brány 2 nastává při elektrické délce vázaného vedení právě čtvrt vlny. Při dodržení této podmínky rovněž nedochází k vazbě mezi branami 3 a 2.

To lze splnit pouze tehdy, realizujeme-li odbočnici ve vedení s vlnou TEM (např. symetrickém páskovém vedení). Na ostatních vedeních nemá sudý vid stejnou vlnovou délku jako lichý vid. To zhoršuje výsledné vlastnosti odbočnice. Zpravidla pak postupujeme tak, že délku vázaného vedení stanovíme podle průměrné hodnoty vlnové délky pro oba vidy.

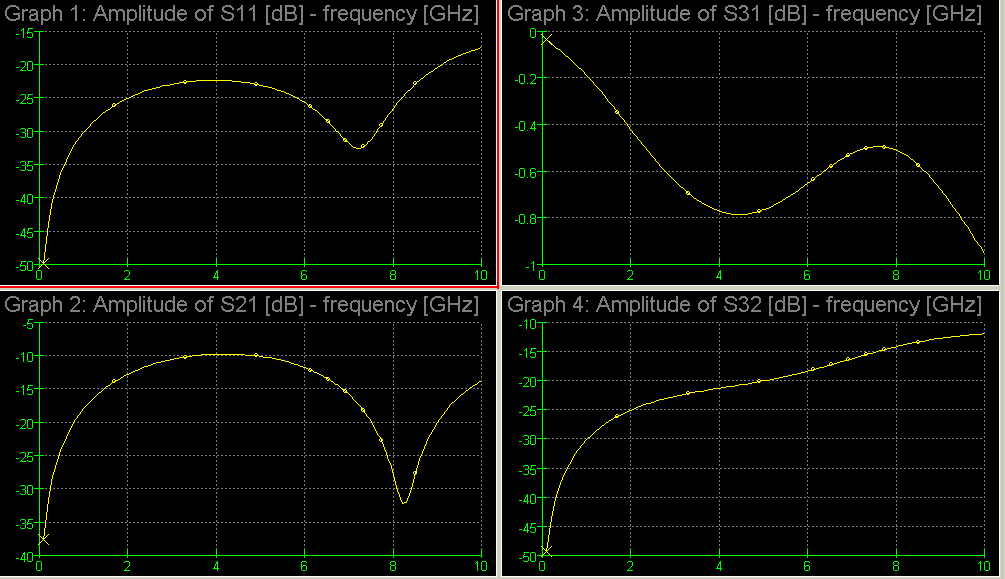Obr. 9.2A.19

Vypočtená charakteristika mikropáskové odbočnice (simulace programem WinMIDE).

Obr. 9.2A.20

Odbočnice provedená v mikropáskvém vedení. Vstupní brána vpravo, výstupní vlevo, odbočení nahoře. Horní vedení vlevo zakončeno odporem SMD.

Označíme-li Zve charakteristickou impedanci sudého vidu a Zvo charakteristickou impedanci lichého vidu vázaného vedení, Z_v charakteristickou impedanci napájecích vedení, pak pro rozptylové parametry odbočnice máme [29]

S_{11} = \frac{R_{e}}{2} (1 - \frac{1 - R_{e}^{2}}{\exp (2 α_{e} l) \exp (2 j β_{e} l) - R_{e}^{2}}) + \frac{R_{0}}{2} (1 - \frac{1 - R_{0}^{2}}{\exp (2 α_{0} l) \exp (2 j β_{0} l) - R_{0}^{2}})

( 9.2A.7 )

S_{12} = \frac{R_{e}}{2} (1 - \frac{1 - R_{e}^{2}}{\exp (2 α_{e} l) \exp (2 j β_{e} l) - R_{e}^{2}}) - \frac{R_{0}}{2} (1 - \frac{1 - R_{0}^{2}}{\exp (2 α_{0} l) \exp (2 j β_{0} l) - R_{0}^{2}})

( 9.2A.8 )

S_{13} = \frac{1}{2} (\frac{(1 - R_{e}^{2}) \exp (2 α_{e} l) \exp (2 j β_{e} l)}{\exp (2 α_{e} l) \exp (2 j β_{e} l) - R_{e}^{2}}) + \frac{1}{2} (\frac{(1 - R_{0}^{2}) \exp (2 α_{0} l) \exp (2 j β_{0} l)}{\exp (2 α_{0} l) \exp (2 j β_{0} l) - R_{0}^{2}})

( 9.2A.9 )

S_{14} = \frac{1}{2} (\frac{(1 - R_{e}^{2}) \exp (2 α_{e} l) \exp (2 j β_{e} l)}{\exp (2 α_{e} l) \exp (2 j β_{e} l) - R_{e}^{2}}) - \frac{1}{2} (\frac{(1 - R_{0}^{2}) \exp (2 α_{0} l) \exp (2 j β_{0} l)}{\exp (2 α_{0} l) \exp (2 j β_{0} l) - R_{0}^{2}})

( 9.2A.10 )

kde jsme označili

R_{e} = \frac{Z_{v e} - Z_{v}}{Z_{v e} + Z_{v}}

R_{0} = \frac{Z_{v 0} - Z_{v}}{Z_{v 0} + Z_{v}}

Přitom α a β jsou po řadě imaginární a reálná část konstanty šíření, přičemž index e nebo o označuje sudý nebo lichý vid, l je délka vázaného vedení.

Pro ideální směrovou odbočnici platí [31] S₁₁ = S₁₄ = 0, takže

R_{e} = - R_{0}

β = 0

Z_{v} = \sqrt{Z_{v e} Z_{v 0}}

( 9.2A.11 )

Pro požadovanou vazbu C [dB] je pak třeba dodržet [32]

Z_{v e} = Z_{v} \sqrt{\frac{1 + 10^{- C / 20}}{1 - 10^{- C / 20}}}

Z_{v 0} = Z_{v} \sqrt{\frac{1 - 10^{- C / 20}}{1 + 10^{- C / 20}}}

( 9.2A.12 )

Zpět