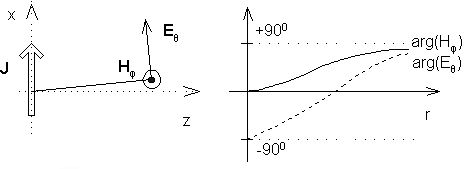Multimediální učebnice

Huygensův princip

Matematické vyjádření Huygensova principu, jak bývá obvykle uváděno v učebnicích, není jeho úplnou formou. Tím je míněno, že užití je omezeno jen na případ, kdy v každém místě apertury platí mezi výsledným elektrickým a magnetickým polem přímá úměra (tj. můžeme psát H = E / Z). Takový případ nastává například na otevřeném konci vlnovodu, kde lze s dostatečnou přesností prohlásit, že pro elektrickou a magnetickou intenzitu platí

E^{t o t} = E^{i n c} (1 + ρ_{0})

H^{t o t} = H^{i n c} (1 + ρ_{0})

H^{i n c} = \frac{E^{i n c}}{Z_{g}}

( 1 )

kde horní index inc značí intenzitu vlnění dopadajícího na otevřený konec vlnovodu a horní index tot značí intenzitu výsledného vlnění (součet dopadající a odražené vlny). Dále, ρ₀ je činitel odrazu a

Z_{g} = \frac{Z}{\sqrt{1 - {(\frac{λ_{0}}{λ_{m} \sqrt{ε_{r}}})}^{2}}}

( 2 )

je impedance vidu TE₁₀ v obdélníkovém vlnovodu; Z je charakteristická impedance prostředí uvnitř vlnovodu, λ_m = 2a je mezní vlnová délka pro případ, kdy je vlnovod bez dielektrika a a je rozměr delší strany vlnovodu. Dále se ve vztahu pro Z_g vyskytuje vlnová délka ve vakuu λ₀ a relativní permitivita prostředí ve vlnovodu ε_r. Pro vid TE₁₀ bude mít elektrická intenzita jen složku E_y a magnetická intenzita naopak složku H_x.

Dosadíme-li hodnoty E^tot a E^tot/Z_g do úplného vztahu pro Huygensův princip, dostaneme po několika úpravách známé, zjednodušené vyjádření Huygensova principu (vztah pro přepočet velikosti elektrické intenzity na plošce E^(S) do libovolného bodu ležícího ve vzdálené oblasti)

E^{(P)} = \frac{j}{λ} \int_{- a / 2}^{+ a / 2} \int_{- b / 2}^{+ b / 2} E^{(S)} \cos (n, r_{2}) \frac{\exp (- j k r)}{r_{2}} d y d x

( 3 )

kde a a b jsou rozměry ozářené plošky, λ značí vlnovou délku v uvažovaném prostředí, E^(S) je velikost elektrické intenzity na plošce, k značí vlnové číslo, n značí normálu k plošce a r₂ je polohový vektor mezi ploškou S a bodem pozorování P.

Úplný vztah je možno odvodit z Maxwellových rovnic pro elementární plošku, na níž je známa hustota elektrických a magnetických proudů. Pro vzdálenou oblast dostáváme

E_{ϑ}^{s} = - j \frac{k}{4 π} (η J \cdot T_{x y z ϑ} + K \cdot T_{x y z φ}) \frac{\exp (- j k r)}{r}

( 4a )

E_{φ}^{s} = - j \frac{k}{4 π} (η J \cdot T_{x y z φ} + K \cdot T_{x y z ϑ}) \frac{\exp (- j k r)}{r}

( 4b )

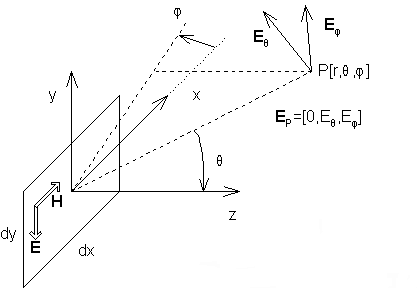
Obr. A.1

Souřadné systémy, vystupující v odvození úplného Huygensova principu

K vysvětlení (4a,b) slouží obr. 1. Ten ukazuje elementární plošku o rozměrech dx a dy, na které tečou elektrický proud J a proud magnetický K. Elektrická intenzita rozptýlené vlny E^s, tj. intenzita vytvořená ozářenou ploškou v bodě r, je vyjádřena v kulových souřadnicích. Dále předpokládáme, že hustota proudů J a K je známa v kartézském vyjádření. Vztahy pro E_ϑ^s a E_φ^s obsahují vektory T, které provádí transformaci z kartézské soustavy do soustavy kulové:

T_{x y z φ} = [\begin{matrix} - \sin (φ) & \cos (φ) & 0 \end{matrix}]

( 5a )

T_{x y z ϑ} = [\begin{matrix} - \cos (ϑ) \cos (φ) & \cos (ϑ) \sin (φ) & - \sin (ϑ) \end{matrix}]

( 5b )

Proudy J a K na elementární plošce nemusejí fyzicky téci; jde o tzv. ekvivalentní proudy, jejichž zdrojem je elektrické a magnetické pole v rovině plošky. Tyto proudy lze vypočíst dle

J = n \times H

( 6a )

K = - n \times E

( 6b )

kde n je normála k elementární plošce (totožná s jednotkovým vektorem u_z).

Pomocí vztahů (6a,b) je možné v reálném případě spočítat hustotu proudů tekoucích po elektrické a magnetické stěně. Námi vyšetřovaná ozářená ploška však fyzicky nemusí být ani elektrickou ani magnetickou stěnou.

Pro přímou aplikaci principu musí být splněna podmínka, že v poloprostoru vymezeném ploškou a kladným směrem vektoru z nejsou přítomny další objekty. Pokud tato podmínka není splněna, lze Huygensův postup a princip ekvivalentních proudů použít, ale situace se komplikuje odrazy od těchto objektů, jež zpětně ovlivňují ozáření elementární plošky. Tímto případem se zde nebudeme zabývat.

Díky tomu, že při výpočtu ekvivalentních proudů počítáme vektorové součiny n × E, n × H (n je normála k plošce), výpočtu proudů J a K stačí jen znalost těch složek E a H, které jsou tečné k elementární plošce.

Posledním symbolem, jehož význam nebyl vysvětlen, je charakteristická impedance volného prostoru η.

Tolik tedy k úplnému tvaru Huygensova principu. V následujících odstavcích ukážeme, jak je možné tento tvar zjednodušit v případě, kdy na rovinné plošce známe elektrickou intenzitu a intenzita magnetická je s ní svázána prostřednictvím impedance (to platí např. pro otevřené ústí vlnovodu, ale nikoli např. v případě povrchu mikropáskové antény, protože její povrchová impedance není konstantou).

Dříve než přistoupíme k popsanému zjednodušení, uvedeme několik poznámek k znaménkům ve vztazích (4a,b). Pečlivý čtenář si jistě všiml znamének minus na začátku pravé strany v těchto vztazích. Znaménko minus v (4a) se změní na plus, pokud vyjádříme-li H pomocí –E/Z_g (viz. směr E a H v obr. 1). Konkrétně to bude vidět na následujícím příkladě.

Mějme elementární elektrický dipól s proudovou hustotou J. Uvažujme, že proud teče ve směru x. Pokud budeme uvažovat složku E, která je rovnoběžná s proudem J, pak musí ve vzdálené oblasti platit úměra E ~ +jJ. Situaci ukazuje obr. 2.

Obr. A.2

K vysvětlení znamének v úplném Huygensově principu

Dále se podívejme, jak to vypadá s magnetickou intenzitou a jaké je chování E, H v blízké zóně elementárního dipólu. Na obr. 2 je kromě směru E zakreslen také směr H. Komplexní amplituda složek E_ϑ a H_φ závisí na vzdálenosti r následovně:

E_{ϑ} \approx \frac{j}{k r} + \frac{1}{{(k r)}^{2}} - \frac{j}{{(k r)}^{3}},

H_{φ} \approx \frac{j}{k r} + \frac{1}{{(k r)}^{2}}

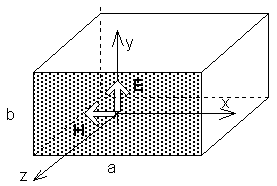
Magnetické pole na povrchu dipólu (vzhledem k velmi malé vzdálenosti dominuje člen 1/k²r²) je ve fázi s proudem. Naopak pole elektrické (dominuje -j/k³r³) je fázově posunuto o – 90°. Naopak ve vzdálené oblasti (vzhledem k velké vzdálenosti dominují členy j/kr) se fáze obou složek rovnají (90°). Průběh fáze složek E_ϑ a H_φ naznačen na obr. 2.

Snad na závěr je dobré zmínit se o vymezení blízké oblasti. U elementárního dipólu je tato oblast vymezena vzdáleností λ₀/(2π), kdy amplituda podélné složky elektrické intenzity E_r a složky příčné E_ϑ nabývají stejných hodnot.

Nyní se věnujme odvození zjednodušeného Huygensova principu (vztahy pro E_ϑ a E_φ).

Uvažujme otevřený konec vlnovodu (obr. 3). Vlnovodem se šíří vid TE₁₀. Výslednou elektrickou intenzitu na otevřeném konci značíme E, intenzitu magnetickou H. V obr. 3 jsou rovněž uvedeny vztahy mezi intenzitami E a H a proudovými hustotami J a K.

J_{e k v} = n \times H = - \frac{E}{Z} = \frac{(- E_{x}, - E_{y},0)}{Z} = \frac{(0, - E_{y},0)}{Z}

K_{e k v} = - n \times E = (E_{y}, - E_{x},0) = (E_{y},0,0)

Obr. A.3

Zjednodušení obecného Huygensova principu pro otevřené ústí vlnovodu

Nyní můžeme dosadit za J a K do úplného vztahu pro E_ϑ a E_φ. Prozatím však předpokládejme, že E a H jsou navzájem kolmé, ale mají nenulové složky x a y. Na závěr odvození bude od tohoto předpokladu upuštěno.

Popsaným dosazením a integrací příspěvků od všech elementárních plošek dostaneme

E_{ϑ}^{s} = - j \frac{k}{4 π} \frac{\exp (- j k r)}{r} \int_{S} {η [\begin{matrix} - E_{x} & - E_{y} \end{matrix}] [\begin{matrix} \cos (ϑ) \cos (φ) \\ \cos (ϑ) \sin (φ) \end{matrix}] + [\begin{matrix} E_{y} & - E_{x} \end{matrix}] [\begin{matrix} - \sin (φ) \\ \cos (φ) \end{matrix}]} d S

( 7a )

E_{ϑ}^{s} = \frac{j}{2 λ} \frac{\exp (- j k r)}{r} [1 + \frac{η}{Z} \cos (ϑ)] [N_{x} \cos (φ) + N_{y} \sin (φ)]

( 7b )

kde N_x, N_y jsou dvojné integrály, které formují vlastní funkci záření otevřeného ústí vlnovodu

N_{x} = \int_{S} E_{x} \exp (- j k Δr) d S

N_{y} = \int_{S} E_{y} \exp (- j k Δr) d S

Analogicky se postupuje i v případě složky Eφ

E_{φ}^{s} = - j \frac{k}{4 π} \frac{\exp (- j k r)}{r} \int_{S} {η [\begin{matrix} - E_{x} & - E_{y} \end{matrix}] [\begin{matrix} - \sin (φ) \\ \cos (φ) \end{matrix}] + [\begin{matrix} - E_{y} & E_{x} \end{matrix}] [\begin{matrix} \cos (ϑ) \cos (φ) \\ \cos (ϑ) \sin (φ) \end{matrix}]} d S

( 8a )

E_{φ}^{s} = \frac{j}{2 λ} \frac{\exp (- j k r)}{r} [1 + \frac{η}{Z} \cos (ϑ)] [N_{x} \sin (φ) - N_{y} \cos (φ)]

( 8b )

Při odvození vztahů (8a,b) jsme předpokládali, že se bod pozorování nachází ve vzdálené oblasti. Proto bylo možno vytknout exponenciální člen před integrál a při integraci uvažovat pouze dráhové rozdíly Δr.

Jak bylo zmíněno, pro otevřené ústí se situace ještě dále zjednoduší, neboť složka E_x bude nulová, a tedy i N_x bude rovno nule.

Na závěr ještě dvě poznámky:

Zjednodušený vztah pro Huygensův princip předpokládá, že se do něj bude dosazovat pouze intenzita dopadající vlny E^inc (resp. H^inc) a výsledná intenzita bude přibližně plus nebo minus dvojnásobek (to přibližně platí pro otevřené ústí a f >> f_krit a platí to přesně pro dokonalou elektrickou plochu). Tak je možné vysvětlit nepřítomnost dvojky v zjednodušeném vztahu pro Huygensův princip.
Zjednodušený vztah pro Huygensův rovněž obsahuje pouze člen cos(ϑ) namísto správného (1 + η cos(ϑ)/Z). Zjednodušený Huygensův princip tedy zavádí pouze jakousi aproximaci skutečné směrové charakteristiky. Taková aproximace není na závadu při určování šířky svazku, ale je nepřípustná, pokud sledujeme úroveň postranních laloků antény. V takovém případě je nutné užít vztahy výše uvedené.