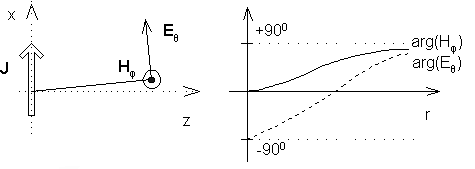Huygens principleMathematical expression of Huygens principle, as usually presented in classical textbooks, is not of a complete form: its exploitation is limited to the case when the intensity of the total magnetic field H is directly related to the intensity of the total electric field E in every point of the space (i.e., we can write H = E / Z). The described situation appears at the open end of a waveguide where intensity of electric field is related (with sufficient accuracy) to the intensity of magnetic field according to the following expressions.
Here, the upper index inc denotes intensity of incident wave arriving to the open end of a waveguide and the upper index tot denotes intensity of the total field (summation of the incident wave and the reflected one). Further, ρ0 is reflection coefficient and
is impedance of the mode TE10 in a rectangular waveguide; Z is characteristic impedance of the environment inside a waveguide, λm = 2a is critical wavelength for a waveguide without dielectrics and a is the dimension of a longer side of a waveguide. Next, λ0 denotes wavelength in the vacuum and εr is the relative permittivity in the waveguide. Considering the mode TE10, only the component Ey of the intensity of electric field, and only the component Hx of the intensity of magnetic field are non-zero.. Substituting Etot and Etot/Zg the complete relation of Huygens principle, we obtain a well-known, simplified expression of Huygens principle (relation for re-computing magnitude of the intensity of electric field on an elementary surface E(S) to an arbitrary point, which is located in the far-field region)
Here, a and b denote dimensions of an elementary irradiated surface, λ is wavelength in a given environment, E(S) is magnitude of the intensity of electric field on an elementary surface, k denotes wavenumber, n is a vector perpendicular to an elementary surface and r2 is the position vector between an elementary surface S and an observation point P. The complete relation can be derived from Maxwell equations for an elementary surface, where electric current density and magnetic current density are known. For the far-field region, we get
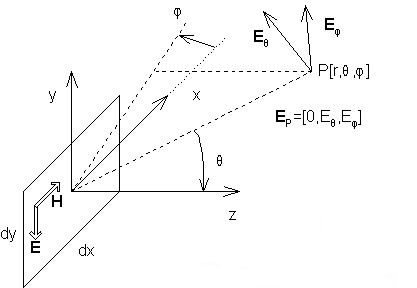
Eqn. (4a,b) is explained in fig. 1. Here, an elementary surface of dimensions dx and dy, where electric current J and magnetic current K are flowing, is depicted. Electric intensity of scattered field Es, i.e. intensity created by the irradiated elementary surface in the point r, is expressed in spherical coordinates. Next, current densities J and K are supposed being known in a Cartesian coordinate system. Relations for Eϑs and Eφs contain vectors T, which perform transformation from Cartesian coordinate system to spherical one:
Currents J and K do not need to physically flow on an elementary surface (we speak about so called equivalent currents, which are induced by electric field and magnetic one on the elementary surface). These currents can be evaluated using
Here, n is perpendicular to the elementary surface (identical with the unitary vector uz). Using eqns. (6a,b), current densities flowing on electric and magnetic walls can be computed in a real case. Unfortunately, an examined irradiated surface does not need being neither electric nor magnetic one. Direct application of the described principle is conditioned by the requirement that no other objects are present in a half-space defined by the elementary surface and the positive direction of vector z. If this condition is not met, Huygens approach and principle of equivalent currents can be applied, but the situation is complicated by reflections from those objects which further influences irradiation of the elementary surface. This case is not analyzed here. Thanks to the fact that vector products n × E, n × H (n is perpendicular to the surface) are computed when evaluating equivalent currents, only those components of currents J and K have to be known, which are tangential to the elementary surface. The last symbol, which has not been explained yet, is free-space characteristic impedance η. That is the end of a brief note on the complete form of Huygens principle. In the following paragraphs, we show the simplification of the complete form in the case when electric intensity is known on an elementary surface and magnetic intensity is related to it via impedance (this approach can be used for an open end of a waveguide but it cannot be applied to a surface of a microstrip antenna because its surface impedance is not constant). Before performing the described simplification, let us turn our attention to the signs in eqns. (4a,b). Note that the right-hand sides of those relations start by the sign minus. The sign minus in (4a) is changed to plus if H is expressed as –E/Zg (see direction of E and H in fig. 1). This is further explained by the following example. Assume an elementary electric dipole with current density J. The current is expected to flow in the direction x. Considering such component of E, which is oriented in parallel with the current J, then the relation E ~ +jJ has to be valid in the far-field region. Fig. 2 illustrates the situation.
Now, let us investigate the situation of magnetic intensity and the behavior of E, H in the near-field zone of an elementary dipole. In fig. 2, both the vector E and the vector H are depicted. Complex amplitude of components Eϑ and Hφ depend on the distance r by the following way:
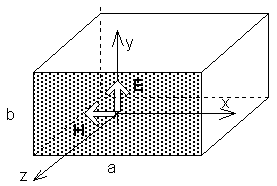
Magnetic field on the surface of the dipole (thanks to the small distance r, the term 1/k2r2 is dominant) is of the same phase than the current. On the contrary, phase of electric field (the term -j/k3r3) is dominant) is shifted for 90°. In the far-field zone, (thanks to the large distance r, the terms j/kr are dominant) phase of both components is identical (90°). Phase course of Eϑ and Hφ is depicted in fig. 2. Dealing with the near-field zone of an elementary dipole - the zone is given by the distance λ0/(2π), where the amplitude of the longitudinal component Er and the amplitude of the transversal one Ej are of the same magnitude. Now, let us concentrate on the derivation of the simplified Huygens principle (relations for Eϑ and Eφ). Assume an open end of a waveguide (fig. 3). In the waveguide, mode TE10 propagates. The electric intensity of the total field at the end of the waveguide is denoted by E, the magnetic intensity by H. In fig. 3, even relations among intensities E and H and current densities J and K are given.
Let us substitute for J and K to the complete relation for Eϑ and Eφ, and assume this moment that E and H are mutually perpendicular and their components x and y are non-zero. At the end of the derivation, this assumption will be cancelled. The described substituting and integrating waves from all the elementary surfaces yield
Here, Nx, Ny are double integrals, which form own radiation pattern of the open end of the waveguide
Analogically for the component Eφ
When deriving eqns. (8a,b), the observation point was expected in the far-field region. We could therefore take the exponential term out of the integral and we integrated space shifts Δr only. In the case of the open end of the waveguide, the situation becomes even simpler because the component Ex is zero, and therefore even Nx is zero. And finally, two concluding notes:
|