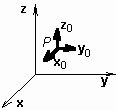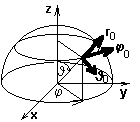Slovník pojmůAmpérův zákonAmpérův zákon celkového proudu nám říká, že součet vodivého proudu indukovaného Iind, vodivého proudu vnuceného zdroji Ivn a proudu posuvného dψ/dt, které procházejí v kladném směru plochou ohraničenou uzavřenou křivkou l, je roven cirkulaci vektoru intenzity magnetického pole H po této křivce
Cirkulace vektoru, neboli křivkového integrálu vektoru A po uzavřené křivce l, se přitom není třeba bát. Cirkulaci si totiž můžeme představit jako součet skalárních součinů vektoru A a vektoru elementárního úseku křivky dl v určitém počtu bodů na křivce l. Čím více takových bodů bude, tím blíže bude mít naše představa ke skutečné cirkulaci. Anténa Yagi, reflektor, direktorYagiho anténa se skládá z jednoho aktivního prvku a několika prvků pasivních. Aktivním prvkem je symetrický dipól (nebo dipól skládaný), který většinou pracuje ve čtvrtvlnné rezonanci. Pasivní prvky jsou tvořeny dipóly bez napájecí štěrbiny. Jeden pasivní prvek, jehož délka je větší než délka aktivního prvku a jenž je umístěn vzadu, hraje roli reflektoru. Ostatní pasivní prvky, které jsou kratší než aktivní prvek a které jsou umístěny vpředu, jsou tzv. direktory. Besselova rovnice, Besselova funkce, Neumannova funkcePři řešení vlnové rovnice ve válcových a kulových souřadnicích metodou separace proměnných dostáváme pro jednu proměnnou (radiální souřadnici) Besselovu diferenciální rovnici
Čárkou je označena derivace podle proměnné x. Pokud ν není celé číslo, je řešením rovnice lineární kombinace Besselových funkcí řádu ν a řádu -ν
V úlohách, v nichž je ν = n celé číslo, jsou řešení Jν(x) a J-ν(x) lineárně závislá a jako druhý partikulární integrál musíme použít Neumannovu funkci Nn(x)
Biot-Savartův zákonSíla, kterou na sebe působí elektrické bodové náboje v pohybu, je nazývána silou magnetickou. Silové pole, jenž kolem sebe vytváří náboj v pohybu, je nazýváno polem magnetickým. Magnetické pole bodového náboje Q1, pohybujícího se rychlostí v1, je kvantifikováno magnetickou indukcí B. Magnetická indukce je dána Biot-Savartovým zákonem Magnetická indukce udává, jakou silou by působil bodový náboj Q1, pohybující se rychlostí v1, na jednotkový bodový náboj v bodě r, pohybující se jednotkovou rychlostí. Symbol μ0 značí permeabilitu vakua (μ0 = 1.26× 10-6 H× m-1). Bodový zdrojBodovým zdrojem rozumíme takový zdroj elektromagnetického vlnění, jehož jedinou vlastností je schopnost vyzařovat. Zdroj má nulovou hmotnost a nulové rozměry. Bázová funkce (kapitola 4,6)Bázovou funkcí rozumíme funkci, která tvoří bázi (jakousi základnu) pro aproximaci neznámé, hledané funkce. Mezi nejčastěji používané bázové funkce patří po částech konstantní funkce (každá funkce nabývá jednotkové hodnoty na právě jedné diskretizační buňce a na ostatních buňkách je nulová) a po částech lineární funkce. Charakteristická impedanceCharakteristická impedance Z0 je důležitý parametr vedení. Pokud je vedení zakončeno impedancí komplexně sdruženou s impedancí Z0, je veškerá energie přenášená vedením spotřebována v ukončovaní impedanci (nedochází k odrazům). Pokud je ukončovací impedance odlišná, část energie je v ní spotřebována a část se ve formě odražené vlny vrací zpět ke zdroji. Odražená vlna se skládá s vlnou přímou a na vedení vzniká stojaté vlnění. Charakteristická impedance je také rovna poměru napětí a proudu postupné vlny. Na bezeztrátovém vedení je Z0 reálná, u běžných vedení má malou imaginární složku. Hodnota charakteristické impedance vedení závisí na příčných rozměrech vedení, na jeho tvaru a na dielektriku. Coulombův zákonMějme ve vakuu ve vzdálenosti d od sebe umístěny dva bodové náboje Q1 a Q2, které mají opačná znaménka a vzájemně jsou v klidu. Tyto dva náboje se budou přitahovat silou o velikosti
Uvedený vztah je vyjádřením Coulombova zákona. Symbol π v něm značí Ludolfovo číslo a ε0 je permitivita vakua (ε0 = 8.85× 10-12 F× m-1). De-embeddingUvedeným termínem označujeme postup, kdy se z napětí a z proudu dodaného lokalizovaným zdrojem pole získává činitel odrazu (resp. činitel přenosu) pro případ buzení mikrovlnného obvodu dlouhými přívody tak, aby byl výsledek získaný momentovou metodou ve shodě s měřením. DifrakceDopadá-li vlnění na těleso, které nemá zřetelně vyjádřenou rozlehlou, rovinnou a hladkou plochu, nedochází sice k odrazu, ale šíření vln je tělesem zřetelně ovlivněno. Příslušný elektromagnetický jev se nazývá difrakce. Český ekvivalent ohyb je sice méně obecný, ale většinou dostatečně výstižný. Hovoří se o ohybu vln za terénní překážku (tj. o difrakci na terénní překážce), o ohybu vln za budovu, na clonkách v optice (tj. o difrakci na těchto objektech) nebo na dešťové kapce (kdyby bylo těch kapek mnoho, bude se jednat o rozptyl). Většinou si totiž můžeme dobře představit, že dráhy (trajektorie) vln jsou v blízkosti těles zakřivené, takže vlnění se dostává i za těleso (i když samo elektromagnetické vlny vůbec nepropouští). Jako difrakci vysvětlujeme i některé jevy, při nichž zakřivení trajektorií není na první pohled zřejmé (např. některé případy vedení vln). Vždy jde však o vzájemné působení elektromagnetické vlny a nějakého hmotného objektu s odlišnými hodnotami elektrických parametrů (permitivity, vodivosti, permeability). Difrakční činitelDifrakční činitel je konstantou úměrnosti mezi amplitudou difrakčních vln a amplitudou vlny dopadající. Diracův impulzDiracův impuls je impulsem nekonečně úzkým (nabývá nenulové hodnoty v jediném bodě) a zároveň nekonečně vysokým (ve zmíněném jediném bodě nabývá nekonečné hodnoty). Velmi významná je tzv. filtrační vlastnost Diracova impulsu
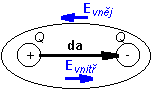
Jelikož Diracův impuls δ (x-x0) nabývá nenulové hodnoty pouze v bodě x0, je výsledkem integrování funkční hodnota funkce f právě v bodě x0. Disperze (kapitola 3)Slovem disperze popisujeme jev, kdy se signály o různých kmitočtech šíří různou rychlostí. Různé kmitočtové složky signálu tak mají na výstupu různá zpoždění, takže jejich složením dostáváme jiný signál nežli signál vstupní (signál na výstupu je zkreslený). Disperze (kapitola 4)Disperze je jev, kdy fázová rychlost vlny v nějakém prostředí není konstantou, ale závisí na kmitočtu. Prostředí, v němž dochází k disperzi, je prostředí disperzní. K disperzi dochází u některých typů vedení (vlnovod, mikropáskové vedení). Když se takovým vedením šíří vlna, složená z několika kmitočtů, bude se každá frekvenční složka šířit jinou rychlostí, takže výstupní signál bude odlišný od signálu vstupního, bude zkreslený. Drátový dipólDipól si můžeme představit jako rovný úsek vodiče, který je uprostřed přerušen napájecí štěrbinkou. Pokud do napájecí štěrbiny umístíme symetrický zdroj harmonického napětí, poteče v jedné půl-periodě do jednoho ramene proud, jehož náboje se budou koncentrovat na konci vodiče. V druhé půl-periodě budou akumulované náboje odtékat zpět do zdroje. Na druhém rameni dipólu bude situace obdobná (v první půl-periodě akumulované náboje odtékají, v druhé půl-periodě se náboje akumulují). Mluvíme-li o drátovém dipólu, předpokládáme kruhový průřez anténního vodiče a velmi malý poloměr tohoto vodiče vzhledem k vlnové délce a k délce dipólu. Dutinový rezonátorDutinové rezonátory patří mezi mikrovlnné rezonanční obvody. Dutinovým rezonátorem může být dielektrikum zcela obecného tvaru, které je uzavřeno vodivým pláštěm. Rezonanční kmitočet je dán rozměry a tvarem dielektrika (dutiny), parametry dielektrika a videm kmitání. Činitel jakosti dutinových rezonátorů se pohybuje v mezích 103 až 105. Dyadická Greenova funkceDyadická Greenova funkce je funkcí úměrnosti mezi vektorem proudové hustoty J a mezi vektorovým potenciálem A. Dyadickou Greenovu funkci si můžeme představit jako matici o rozměru 3 × 3, u níž je každý prvek funkcí. Např. funkce v prvním sloupci a druhém řádku udává příspěvek složky Jx ke složce potenciálu Ay, atd. Efektivní permitivitaAnalýza struktur, které obsahují několik dielektrik (např. substrát a vzduch), je velmi komplikovaná (je třeba brát v úvahu splnění podmínek na rozhraní dielektrik). Proto se při přibližných výpočtech nahrazuje nehomogenní dielektrikum dielektrikem homogenním, a to takovým způsobem, aby vlastnosti původní struktury zůstaly zachovány. Hodnota permitivity tohoto náhradního homogenního dielektrika se označuje termínem efektivní permitivita. EikonálaEikonála je taková skalární funkce souřadnic, jejíž gradient (směr nejstrmějšího spádu funkce) je v každém bodě shodný se směrem šíření vlny. Elektricky tenký substrátUvedeným termínem označujeme dielektrický substrát, jehož tloušťka je mnohem menší ve srovnání s délkou vlny v tomto substrátu. Elementární elektrický dipólUvažujme ideální dielektrikum, tedy prostředí bez volných nábojů. Kladné a záporné náboje, tvořící navenek neutrální atomy dielektrika, se mohou pohybovat jen uvnitř těchto atomů. Necháme-li na naše dielektrikum působit vnější časově neproměnné elektrické pole, uchovají si atomy jako celek nadále svou neutralitu, avšak těžiště kladných a záporných nábojů se posune. Z atomů se stanou elektrické dipóly (atomy budou polarizovány).
Elektrický dipól je popsán momentem elektrického dipólu p [C.m] kde da je polohový vektor od záporného ke kladnému pólu atomu a Q je náboj na pólech. Je-li vnější elektrické pole časově proměnné, bude se odpovídajícím způsobem měnit velikost náboje na koncích dipólu. Můžeme si přitom představit, že tyto změny velikosti náboje jsou způsobeny proudem, tekoucím dipólem (viz rovnice kontinuity). Elementární smyčka, magnetický dipólV každém atomu krouží po orbitech kolem jádra elektrony. Tento pohyb elektronů po orbitech si můžeme představit jako proudovou smyčku, protékanou proudem I. Jelikož náboje v pohybu vytvářejí magnetické pole, popíšeme působení elementární proudové smyčky momentem magnetického dipólu
kde dS je vektor plochy, ohraničené proudovou smyčkou. Ve feromagnetiku způsobuje vnější magnetické pole takové natáčení proudových smyček, že se směr momentů magnetických dipólů blíží směru vnější magnetické indukce. Tím dochází uvnitř materiálu k zesilování vnějšího pole. Elementární smyčku můžeme považovat za nejjednodušší smyčkovou anténu (za elementární magnetický dipól). Evanescentní vlnaEvanescentní vlna vlastně vlnou vůbec není. Fáze se ve směru šíření nemění, protože fázová konstanta je nulová, a amplituda exponenciálně klesá, protože konstanta útlumu je nenulová. Evanescentní vlna se může objevit za určitých podmínek např. na rozhraní dvou prostředí, když jedním z těchto prostředí se šíří (“normální”) vlna rovnoběžně s rozhraním. Ta do druhého prostředí nevniká, ale elektromagnetické pole tam difunduje (evanescentní “vlna”). Fourierova řadaSpektrum signálu s(t), který je periodický s periodou T1, je diskrétní a jeho k-tá složka je dána vztahem
V uvedeném vztahu (Fourierova transformace signálu s) je úhlový kmitočet ω1 = 2π/T1 a hvězdička značí komplexní sdruženost. Známe-li spektrální složky ck, můžeme zpětně rekonstruovat časový průběh signálu
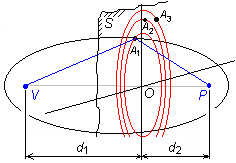
Výše uvedený vztah nazýváme Fourierovou řadou. Fresnelova difrakceTermínem Fresnelova difrakce popisujeme ohyb vlnění, ke kterému dochází při průchodu otvorem v tenké rovinné přepážce; přepážka sama vlnění ani neodráží a ani nepropouští. Fresnelova zónaMějme ve volném prostoru umístěn vysílač V a přijímač P, jak je naznačeno na obrázku. V libovolném rovinném řezu kolmém na spojnici VP nalezněme body A1 tak, aby lomená dráha VA1P byla právě o polovinu délky vlny delší než přímá spojnice VP. Takových bodů je nekonečně mnoho. Leží na kružnici, která má střed v bodě O. Plocha ohraničená touto kružnicí je tzv. první Fresnelova zóna a OA1 = r01 je její poloměr. Stejně můžeme nalézt další body A2, ...An, pro které platí
Plocha mezikruží mezi kružnicemi A2 a A1 je druhá Fresnelova zóna, atd. Poloměr n-té zóny lze vypočítat podle přibližného vzorce
Opakujeme-li popsanou úvahu např. pro body A1 v různých místech (řezech) podél spojnice VP, dostaneme různé hodnoty poloměru první Fresnelovy zóny. Všechny takto získané body A1 leží na rotačním elipsoidu, který se nazývá první Fresnelův elipsoid. Fresnelovy integrályFresnelovy integrály jsou dány vztahem
Jejich hodnotu můžeme vypočíst numerickou integrací v matlabu, můžeme ji najít v tabulkách nebo ji můžeme odečíst z klothoidy. Fázová rychlost (kapitola 2)Fázová rychlost udává, jakou vzdálenost urazí vlnoplocha s fází φ0 za jednu sekundu, tj. (ω je úhlový kmitočet, k’ = Re{k} značí fázovou konstantu). Obvykle měříme tuto vzdálenost rovnoběžně se směrem šíření vlny. V uvedeném vztahu jsou pak k a vf příslušné veličiny ve směru šíření vlny. Fázová rychlost, skupinová rychlost (kapitola 3)Fázová rychlost udává, jak se změní fáze vlny za jednotku času. Fázová rychlost není svázána s rychlostí přenosu energie, a proto může nabývat hodnot vyšších nežli je rychlost světla ve vakuu c = 3× 10+8 m/s. Fázová rychlost je nekonečná ve směrech, které leží na vlnoploše (tj. na ploše, v jejichž bodech má vlna stejnou fázi). Ke změně fáze o 2π radiánů zde totiž dochází během nekonečně krátkého časového intervalu. Naproti tomu skupinová (grupová) rychlost udává, jak rychle je v daném směru přenášena energie. Jelikož ve směrech, které leží na vlnoploše, k přenosu energie nedochází (vlnoplocha je kolmá ke směru šíření), je v těchto směrech skupinová rychlost nulová. Fázová a skupinová rychlost jsou v běžných prostředích vzájemně svázány vztahem
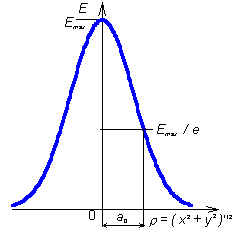
kde vf značí fázovou rychlost, vg je rychlost skupinová a v je rychlost světla ve volném prostoru, který má stejné elektrické a magnetické vlastnosti jako prostředí uvnitř vlnovodu. Galerkinova metoda (kapitola 3)Galerkinovou metodou rozumíme metodu vážených reziduí pro případ, kdy jsou váhovými funkcemi dílčí aproximační funkce. Galerkinova metoda (kapitola 4,6)Galerkinovou metodou rozumíme metodu vážených reziduí pro případ, kdy jsou váhovými funkcemi funkce bázové. Gaussův svazek, Gaussova funkceUvažujme laserový svazek základního vidu TEM00, který ze zdroje vystupuje jako rovnoběžný (vlnoplocha je rovinná a kolmá na směr šíření, na optickou osu). Svazek paprsků není záměrně modulovaný, ale rozložení intenzity pole po příčném průřezu svazku není z podstaty konstantní. U zmíněného vidu je intenzita největší na ose svazku a zmenšuje se k okraji podle Gaussovy funkce:
Zde ρ je radiální vzdálenost od osy svazku a průběh funkce vidíme na obrázku. Svazek s právě popsaným gaussovským příčným rozložením intenzity nazýváme Gaussovým svazkem.
Geometrická optikaGeometrická optika je metoda pro řešení vlnových dějů ve složitějších prostředích, která od klasické geometrické optiky převzala představu o šíření vln podél paprsků. Na rozdíl od klasické geometrické optiky však můžeme navíc počítat i změny amplitudy a fáze intenzity pole a polarizaci vln při šíření prostředím se spojitou změnou parametrů. Geometrická teorie difrakceGeometrická teorie difrakce (GTD) je rozšířením geometrické optiky prostředí s nespojitými nehomogenitami. Řeší se interakce paprsků s tělesy a zákony geometrické optiky se doplní tak, aby se odstranily zjevné nesprávnosti (nespojitosti intenzit na hranici odrazu a stínu), ale aby se zachovaly hlavní přednosti geometrické optiky (představa paprsků). Globální bázová funkceGlobální bázové funkce nabývají nenulových hodnot na celé analyzované oblasti. Jako globální bázové funkce se většinou používají funkce harmonické nebo funkce Besselovy. Greenova funkceGreenova funkce je funkcí úměrnosti mezi vektorem proudové hustoty J a mezi vektorovým potenciálem A. Hankelova funkceBesselově diferenciální rovnici (čárkou je označena derivace podle proměnné x) vyhovuje rovněž lineární kombinace Hankelových funkcí prvního druhu Hn(1)(x) a druhého druhu Hn(1)(x)
Pro Hankelovy funkce platí
Hertzův vektorPředpokládejme, že se nacházíme v ideálním dielektriku, polarizovaném vnějším elektrickým polem. Tato polarizace je popsána vektorem vnucené elektrické polarizace Pvn. Potom můžeme elektrickou indukci vyjádřit jako
Po dosazení elektrické indukce D (1) do prvé Maxwellovy rovnice dostáváme za předpokladu nulového vnuceného proudu Jvn = 0 (indukovaný proud je rovněž nulový, neboť ideální dielektrikum má nulovou vodivost)
a třetí Maxwellova rovnice přejde na tvar
Ze vztahů (2) a (3) získáme vlnové rovnice pro vektorový potenciál
a pro potenciál skalární
Vyjádřeme nyní potenciály A a φ s použitím pomocného vektoru Πe výrazy
Po dosazení (6) do vlnové rovnice (4) a (7) do (5) dojdeme ke vztahům
Určíme-li tedy vektor Πe tak, aby vyhovoval rovnici
jsou zároveň splněny rovnice (8) a (9). Tím jsme pro případ, kdy Jvn = 0, převedli řešení Maxwellových rovnic na řešení jediné nehomogenní rovnice. Tuto možnost objevil Hertz a vektor Πe je označován jako elektrický Hertzův vektor. Duálním postupem lze zavést Hertzův vektor magnetický. Hranové konečné prvkyHranové konečné prvky slouží k aproximaci vektorové funkce v analyzované struktuře. V nejjednodušším případě je vektorová veličina nad plochou každého konečného prvku aproximována lineární kombinací dílčích vektorových funkcí, z nichž každá nabývá na jedné určité hraně trojúhelníkového prvku jednotkové velikosti a směru hrany a na zbývajících dvou hranách hodnoty nulové. Násobíme-li dílčí vektorové funkce velikostí průmětu aproximované veličiny do dané hrany trojúhelníka a sečteme-li popsané součiny
dostaneme aproximaci vektorové veličiny E nad n-tým konečným prvkem E~(n). Ve výše uvedeném vztahu značí Em(n) hranovou hodnotu (velikost průmětu) vektoru E do m-té hrany n-tého trojúhelníkového prvku a Nm(n) je vektorová funkce nabývající jednotkové hodnoty na m-té hraně n-tého prvku a směru této hrany. Huygensův principHuygensův princip říká, že každý bod uzavřené plochy S (přesněji každý její element dS), který je zvnějšku ozářen vlněním, je sám pro oblast uvnitř plochy zdrojem elementární kulové vlny. Huygensův zdrojTermínem Huygensův zdroj označujeme nekonečně malou plošku dS, která je z jedné strany ozářena dopadající elektromagnetickou vlnou. Podle Huygensova principu se tato ploška sama stává zdrojem elektromagnetického vlnění. Skutečné plošné zdroje vlnění (trychtýřové antény, štěrbinové antény, ozářený parabolický reflektor) pak můžeme považovat za soubor Huygensových zdrojů. Hybridní konečné prvkyPři analýze stíněného mikropáskového vedení pomocí hybridních konečných prvků zahrnujeme do výpočtů všechny složky elektrické intenzity nebo všechny složky intenzity magnetické. Podstata hybridních konečných prvků spočívá v modelování podélné složky elektrické nebo magnetické intenzity pomocí uzlové aproximace a v modelování příčných složek elektrické nebo magnetické intenzity pomocí aproximace, založené na hranových vektorech (edge vectors). Impedanční transformátorImpedanční transformátor na vysokých frekvencích plní stejné funkce jako transformátor na nízkých kmitočtech. Transformuje napětí, proud a impedanci. Jen jeho konstrukce je jiná. Nejjednodušším příkladem vysokofrekvenčního impedančního transformátoru je vedení, dlouhé čtvrtinu vlnové délky. Pro takové vedení totiž platí
kde Z0tr2 značí kvadrát charakteristické impedance čtvrtvlnného vedení. Je-li vedení zakončeno impedancí Z0out, pak na jeho vstupu se jeví jako impedance Z0in. Impedanční šířka pásmaImpedanční šířku pásma nejčastěji definujeme jako kmitočtový interval, v němž do antény vstupuje 90% přiváděné energie (10% energie se odráží zpět ke generátoru). Popsané situaci odpovídá poměr stojatých vln přibližně rovný dvěma. Index lomuIndex lomu prostředí je dán poměrem vlnového čísla v daném prostředí a vlnového čísla ve vakuu. V bezeztrátovém prostředí pro index lomu platí
Jinak řečeno – index lomu udává, kolikrát větší je délka vlny ve vakuu než v daném prostředí. Indukované proudyDopadá-li na vodič elektromagnetické vlnění, jsou volné nosiče tímto vlněním uvedeny do pohybu (vznikají indukované proudy). Indukované proudy se samy o sobě stávají zdrojem sekundárního vlnění, které se skládá s vlněním primárním (dopadajícím na vodič). Výsledné vlnění je charakteristické tím, že složka vektoru elektrické intenzity, která je tečná k vodivému povrchu, je velmi malá (v případě dokonalého elektrického vodiče je nulová). Intenzita pole vytvořená Huygensovým zdrojemHuygensův zdroj (nekonečně malá ploška dS) z jedné strany ozářený vlnou s intenzitou E(S), který je součástí větší rovinné plochy (rovněž ozářené), vytvoří na neozářené straně kulovou vlnu, jež má ve vzdálenosti r intenzitu
Úhel ϑ je úhel mezi normálou k dS a průvodičem k místu pozorování. Interaktivní Smithův diagramSpolu s touto multimediální učebnicí jste obdrželi i interaktivní Smithův diagram. Je to program pro operační systém Microsoft Windows a je součástí programového balíku WinMIDE. V menu "Calculate" programu WinMIDE zvolte Smith Chart. Interaktivní Smithův diagram umožňuje vynášet impedance do Smithova diagramu a navrhovat jednoduché přizpůsobovací obvody. Tyto obvody lze uložit na disk ve formátu schemat programu WinMIDE a dále je použít pro sestavení složitějších obvodů. Ionosferická vrstvaUltrafialové záření Slunce ionizuje atmosférické plyny – molekuly a případně i atomy jsou štěpeny na kladný ion a záporný elektron. Ionizovaná vrstva atmosféry se nazývá ionosféra a je asi od 40 km výše. Koncentrace elektronů v ionosféře se mění s výškou a má zřetelná lokální maxima. Oblasti kolem lokálních maxim nazýváme ionosférickými vrstvami. Dopadá-li na ionosférickou vrstvu elektromagnetická vlna, její trajektorie se ve vrstvě zakřiví a za vhodných podmínek se vlna může obrátit zpět k zemi. Izotropní prostředí, anizotropní prostředíIzotropní prostředí má ve všech směrech stejné elektrické a magnetické vlastnosti (stejnou hodnotu permitivity a stejnou hodnotu permeability). V důsledku toho např. složka Dx elektrické indukce je závislá jen na složce Ex intenzity elektrického pole:
Z matematického hlediska jsou permitivita a permeabilita skalární veličiny. Anizotropní prostředí má v různých směrech různé vlastnosti. V důsledku toho např. složka Dx elektrické indukce je (v obecném případě) závislá na všech třech složkách elektrické intenzity:
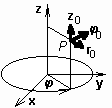
Z pohledu matematiky jsou permitivita a permeabilita tenzory, tj. matice o rozměru 3 × 3. Anizotropním prostředím je např. plasma, v níž existuje stejnosměrné magnetické pole, nebo ferit se stejnosměrnou magnetizací. Kartézská souřadná soustavaJe tvořena třemi přímočarými vzájemně kolmými bázovými vektory x0, y0, z0 (viz obrázek). Libovolný bod je v tomto souřadném systému popsán vektorem
Diferenciální operátory jsou v kartézském souřadném systému popsány následujícími vztahy:
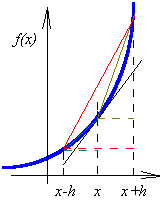
KaustikaPředpokládejme, že vlnění z bodového zdroje se šíří prostředím s relativní permitivitou 1, a z něho vstupuje do vrstvy, ve které permitivita nejprve klesá do jistého minima a pak opět roste k hodnotě 1. V jisté části popsané vrstvy pak dochází k tomu, že se paprsky otáčejí obloučky zpět ke zdroji. Vrcholky těchto obloučků je možné spojitmyšlenou plochou, přes kterou žádný paprsek nepřejde a (těsně) pod kterou se dva sousední paprsky protínají. Tato plocha se nazývá kaustika. KlothoidaKlothoida je grafickým vyjádřením Fresnelových integrálů. Na vodorovné ose je vynesena reálná část výsledku integrování C(x), na svislé ose se nachází část imaginární S(x). V popsaném souřadném systému mají potom Fresnelovy integrály tvar spirálové křivky, která je cejchována parametrem x. Chceme-li vyčíslit Fresnelovy integrály pro určitou hodnotu argumentu x0, najdeme tuto hodnotu na spirálové křivce a na vodorovné a svislé ose přímo odečítáme hodnoty integrálů C(x0) a S(x0). Kmitočtově selektivní povrchKmitočtově selektivní povrch (frequency-selective surface) si můžeme představit jako velmi rozlehlou dielektrickou desku, která má na své lícní straně rozmístěny (ekvidistantně nebo neekvidistantně) planární vodivé elementy a která má rubovou stranu zcela volnou (tj. bez pokovení). Planární vodivé elementy na líci mohou být přitom různě tvarovány, avšak v rámci jednoho kmitočtově selektivního povrchu bývají většinou všechny vodivé elementy stejné. Vodivé elementy mohou být přitom kovové (elektricky vodivé elementy) nebo mohou být realizovány jako štěrbiny ve zcela pokovené lícní straně (magneticky vodivé elementy). Pokud na lícní stranu povrchu dopadají harmonické rovinné vlny o různých kmitočtech, některé jsou povrchem propouštěny s minimálním útlumem, některé jsou zcela odráženy zpět do poloprostoru, z něhož na povrch dopadají, a některé jsou povrchem částečně propouštěny a částečně odráženy zpět. Povrch tedy vykonává kmitočtovou selekci dopadajících vln. Koeficient odrazu, koeficient prostupuKoeficient odrazu je definován jako poměr velikosti určité složky vektoru intenzity vlny, odražené od nehomogenity, k velikosti téže složky vektoru elektrické intenzity vlnění dopadajícího. Pod pojmem nehomogenita máme zde na mysli nějaký objekt, který je dostatečně rozlehlý ve směru příčném ke směru šíření vlny, takže ho vlna nemůže obejít, ale musí jím projít. Objekt má jiné elektrické parametry nebo jinou strukturu než prostředí, kterým se vlna šíří. U prostupu dělíme velikost určité složky intenzity vlny, která nehomogenitou prošla. Je tedy zřejmé, že činitel odrazu a činitel prostupu nabývají hodnot od nuly (nic se neodrazilo, nic neprošlo) do jedničky (všechno se odrazilo, všechno prošlo). Pokud je nehomogenity bezeztrátová, musí být součet činitele odrazu a činitele prostupu roven jedné. Koherentní zářeníZáření nazveme časově koherentním, pokud pro zvolený časový interval Δt naměříme kdekoli a kdykoli stejný fázový posuv Δφ. Záření je prostorově koherentní, pokud pro zvolenou vzdálenost Δl naměříme kdekoli a kdykoli stejný fázový posuv Δφ. Kolmá polarizace, rovnoběžná polarizacePolarizace popisuje, jak je u vlnění orientován vektor intenzity elektrického pole. Při šíření vlny v blízkosti roviny rozhraní dvou prostředí rozlišujeme polarizaci kolmou a polarizaci rovnoběžnou. Nejprve definujme rovinu dopadu: to je rovina kolmá k rovině rozhraní a současně rovnoběžná se směrem šíření vlny. Kolmo polarizovaná vlna má vektor E kolmý na rovinu dopadu, rovnoběžně polarizovaná vlna má vektor E rovnoběžný s rovinou dopadu. Je-li rovinou rozhraní rovina zemského povrchu, pak se často pro kolmo polarizovanou vlnu používá termín vlna horizontálně polarizovaná, pro vlnu rovnoběžně polarizovanou vlnu termín vlna vertikálně polarizovaná. Kolokační metodaKolokační metodou rozumíme metodu vážených reziduí pro případ, kdy jsou váhovými funkcemi Diracovy impulsy. Konečné diferenceKonečné diference používáme k nahrazení hodnoty derivace v případech, kdy derivaci funkce nemůžeme vypočíst. Derivace funkce f v bodě x udává směrnici tečny k funkci v daném bodě (na obrázku naznačeno černou čárou. Přibližnou hodnotu směrnice můžeme určit červeného pravoúhlého trojúhelníka jako
Diferencování, kdy bod x leží uprostřed výpočetního intervalu, nazýváme středovým (centrálním) diferencováním. Vidíme, že směrnice červené a černé přímky jsou si velmi blízké. Kromě středového diferencování se můžeme setkat s diferencováním dopředným (tmavě žlutý trojúhelník) a s diferencováním zpětným (modrozelený trojúhelník)
Vidíme, že směrnice modrozelené a tmavožluté přímky se od směrnice tečny liší mnohem výrazněji nežli v případě středové diference. Konečný prvekKonečný prvek označuje prostorový diskretizační element, na němž sledovaná veličina nabývá konečné energie. Konečný prvek tedy může být i nekonečně veliký, pokud na něm hodnota sledované veličiny dostatečně rychle klesá k nule. Např. energie elektromagnetického pole je na nekonečně velkém konečném prvku, pokrývajícím oblast, která začíná v dostatečně velké vzdálenosti od zdroje a končí v nekonečnu, je konečná. V jednorozměrném případě volíme za konečný prvek úsečku (sledovanou veličinu aproximujeme nad konečným prvkem úsečkou, danou hodnotami veličiny v krajních bodech úsečky), ve dvojrozměrném trojúhelník (aproximační rovina nad konečným prvkem je dána funkčními hodnotami sledované veličiny ve vrcholech) a v případě trojrozměrném čtyřstěn. Konstanta šíření, měrný útlum, měrná fázeSoučinitel přenosu (konstanta šíření) γ popisuje změnu amplitudy a změnu fáze vlnění v podélném směru vlnovodu. Součinitel přenosu je dán vztahem
kde β má význam měrného útlumu a α je měrná fáze (fázová konstanta). Měrný útlum nám říká, k jakému poklesu amplitudy dojde na délce 1 metr; amplituda poklesne na exp(-β) – násobek své počáteční hodnoty. Měrná fáze popisuje změnu fáze vlny na délce 1 metr ve směru šíření vlny (tj. v podélném směru). Kritický kmitočetKritický kmitočet vidu ve vlnovodu udává frekvenci, od které se daný vid začíná vlnovodem šířit. Krystalická mřížkaIdeální krystalická mřížka je modelové uspořádání atomů v objemu materiálu. Toto uspořádání má periodický charakter a lze je popsat elementární buňkou, představující rovnoběžnostěn o hraně a, v němž jsou umístěny jednotlivé částice. Délka hrany a je tzv. mřížková konstanta, která je důležitým parametrem popisu struktury krystalu. Kulová vlnaVlnoplochy kulové vlny jsou kulové plochy. Jejich společný střed je tzv. fázový střed zdroje. Kulovou vlnu můžeme pozorovat v blízkosti bodového zářiče ve volném prostoru (malé antény). Vlnění skutečných (rozměrných) zdrojů kulové není, ale s rostoucí vzdáleností od svého zdroje se postupně mění ve vlnu kulovou. Ve volném bezeztrátovém prostředí je amplituda intenzity pole kulové vlny nepřímo úměrná vzdálenosti od zdroje. Kvazi-statická analýza, vlnová analýzaKvazi-statická analýza mikropáskových vedení spočívá v modelování dominantního vidu (vid kvazi-TEM, šířícího se podél vedení, příčně elektromagnetickou vlnou. Siločáry pole této vlny je možné určit statickou analýzou struktury (na mikropásku uvažujeme napětí jeden volt, na stínicím vlnovodu předpokládáme nulový potenciál). Kvazi-statická analýza dává relativně dobré výsledky v pásmu nízkých mikrovlnných kmitočtů (typicky do 5 GHz). Pokud chceme analyzovat mikropáskové vedení na vyšších kmitočtech, musíme tak učinit pomocí vlnových (angl. full-wave) metod. Ty spočívají v přímém řešení Maxwellových rovnic. Kvazi-statické metodyKvazi-statické metody analýzy planárních mikrovlnných vedení jsou založeny na předpokladu, že dominantní vid vlny, šířící se podél mikropáskového vedení, je možno s dobrou přesností aproximovat příčně elektromagnetickou vlnou (transversal electromagnetic wave, TEM). Potom jsou příčné složky dynamického elektromagnetického pole velmi blízké složkám pole statického, takže přibližné rozložení pole na vedení můžeme získat řešením Laplaceovy rovnice pro skalární potenciál. Křížová polarizaceKřížová polarizace je parametr, který udává poměr mezi užitečnou složku elektrické intenzity v příslušné rovině antény (rovina E nebo rovina H) a složkou elektrické intenzity, která je na tuto složku kolmá. Lagrangeův polynomLagrangeův polynom n-tého stupně obecně vyjádříme pomocí simplexní souřadnice ξ vztahem
kde n je stupeň aproximačního polynomu. Vztah přitom popisuje najednou celou množinu polynomů, přičemž jednotlivé prvky této množiny se liší indexem m, který může nabývat hodnot od nuly po stupeň polynomu n. Nuly polynomů Rm(n) jsou ekvidistantně rozmístěny na souřadnicích ξ = 0, 1/n až (m-1)/n, jednotkové hodnoty polynom nabývá v ξ = m/n. Tudíž, Rm(n) má m ekvidistantně rozmístěných nul nalevo od souřadnice ξ = m/n a žádnou napravo. Lineární anténaLineární anténou rozumíme anténu, kterou je možno složit z konečného počtu elementárních dipólů. Opakem je plošná anténa, kterou skládáme z elementárních Huygensových zdrojů. Lineární kombinaceLineární kombinací vektorů (funkcí) rozumíme takový vektor (takovou funkci), kterou dostaneme sečtením původních vektorů (původních funkcí), vynásobených libovolnými skalárními nenulovými koeficienty. Lineární prostředíPermitivita a permeabilita lineárního prostředí jsou konstanty, nezávislé na intenzitách E a H. Zvyšujeme-li tedy intenzitu elektrického pole, přímo úměrně roste i elektrická indukce. Pokud je zvětšována velikost intenzity pole magnetického, přímo úměrně se zvyšuje magnetická indukce. Lokální bázová funkceLokální bázové funkce nabývají nenulové hodnoty vždy na jedné nebo několika málo diskretizačních buňkách a na zbývajících buňkách jsou nulové. Mezi typické představitele lokálních bázových funkcí patří funkce po částech konstantní nebo po částech lineární. Lorenzova sílaSíla působící na nabitou částici je závislá jen na pozici, rychlosti a množství náboje částice. Pro sílu působící na elementární náboj můžeme psát
kde E a B je elektrické pole a magnetická indukce v místě náboje a v je rychlost částice. Maticová optika, matice svazku, zákon ABCDMatice svazku je matice o rozměru 2×2, která popisuje změnu parametrů Gaussova svazku při průchodu optickým prvkem. Násobíme-li matici zprava sloupcovým vektorem, obsahujícím parametry svazku na vstupu optické soustavy, dostaneme sloupcový vektor parametrů svazku na jejím výstupu. Tento vztah nazýváme zákonem ABCD. Vzhledem k maticové povaze popsaných operací (ty platí pro paraxiální optiku) někdy hovoříme o maticové optice. Metoda indukovaných elektromotorických napětí, činitel vazby, činitel vlastní vazby, vlastní impedance, činitel vzájemné vazby, vzájemná impedanceMetoda umožňuje řešit napěťové, proudové a tedy i impedanční poměry v anténní soustavě. Podle této metody je napětí, které pozorujeme na svorkách jednoho (každého) prvku soustavy, vyvoláno (indukováno) vyzařováním všech prvků soustavy (včetně toho prvku samotného). Lze tedy složit z příspěvků od jednotlivých prvků, z nichž každý je úměrný proudu v příslušném prvku. Např. napětí U1 na svorkách prvního prvku je rovno součtu
kde I1, I2, I3 jsou proudy na svorkách jednotlivých prvků, Z11, Z12, Z13 jsou činitelé vazby mezi prvky. Z11 je činitel vlastní vazby (vlastní impedance), Z1n jsou činitelé vzájemné vazby (vzájemné impedance) mezi prvním prvkem a ostatními prvky v soustavě. Tito činitelé závisejí hlavně na vzájemné poloze a vzdálenosti prvků. Metoda konečných prvkůMetoda konečných prvků je obecnou metodou numerického řešení parciálních diferenciálních rovnic. Metoda konečných prvků sestává z těchto základních kroků:
Metoda vedeníObvykle tak označujeme postup, kdy analýzu složitého objektu (např. antény) si zjednodušíme tím, že aplikujeme (s vědomím určité nepřesnosti) teorii vedení. Metoda slouží např. k modelování vyzařování flíčkové antény. Spočívá v náhradě zářících hran flíčku štěrbinovým vedením. Metoda vedení vyniká jednoduchostí, a přitom umožňuje dosáhnout i poměrně přesných výsledků. Mikropásková anténa se štěrbinovým buzenímMikropáskové anténní zářiče jsou buzeny prostřednictvím štěrbin v zemní ploše. Vlastní napájecí vedení se pak nachází na substrátu, který je umístěný pod substrátem s anténou. Spodní substrát má s horním substrátem společnou zemní plochu se štěrbinou, na lícní (tedy dolní) straně spodního substrátu je pak vytvořeno samotné napájecí vedení. Mikropásková anténa, mikropáskový dipól, flíčková anténa, klasická mikropásková anténaTermínem mikropásková anténa nazýváme souhrnně všechny antény, které jsou vyrobeny mikropáskovou technologií. V naší učebnici do této kategorie spadá mikropáskový dipól (úzký mikropáskový vodič na lícní straně substrátu, který je uprostřed přerušen úzkou štěrbinou, na niž je přivedeno skrze substrát symetrické napájecí napětí) a flíčková anténa (obdélníkový mikropáskový anténní prvek na lícní straně substrátu, který může být napájen mikropáskovým vedení, koaxiálním vedením či štěrbinou v zemní ploše). V české literatuře se pojem flíčková anténa příliš nevžil. Místo tohoto pojmu se používá termínu mikropásková anténa, což vnáší do naší terminologie trochu zmatek. Mikropáskové vedení (kapitola 3)Mikropáskové vedení je tvořeno velmi tenkým a relativně úzkým páskovým vedením, které je umístěno na lícní straně dielektrického substrátu. Spodní (rubová) strana substrátu je souvisle pokovena a slouží jako zemní deska s nulovým potenciálem. Celé vedení bývá většinou umístěno do obdélníkového vlnovodu, který souží jako stínění. Všechny kovové části vedení (mikropásek, zemní deska kovový vlnovod) musejí být přitom vyrobeny z velmi dobrého elektrického vodiče, aby vedení vykazovalo co nejmenší útlum. Z téhož důvodu musí být i dielektrický substrát co nejméně ztrátový. Mikropáskové vedení, zemní plocha (kapitola 4)Mikropáskovým vedením rozumíme vedení, které sestává z relativně úzkého kovového pásku na lícní straně dielektrického substrátu. Rubová strana substrátu je zcela pokovena a má nulový potenciál. Proto rubovou stranu nazýváme zemní plochou. Mikrovlnné kmitočtové pásmoMikrovlnné kmitočtové pásmo je intervalem kmitočtů od 300 MHz do 300 GHz. Těmto kmitočtům odpovídá délka vlny ve volném prostoru (vakuu) od 1 m do 1 mm. Modální analýza planárních anténPři modální analýze planární antény je anténa modelována jako rezonanční dutina, která je zdola i shora ohraničena dokonalými elektrickými stěnami (PEC – perfect electric conductor). Základním předpokladem platnosti modální analýzy je tenký dielektrický substrát. Pokud tloušťka dielektrického substrátu h je mnohem menší než vlnová délka λ, změna elektrického pole ve směru kolmém na kovový flíček (směr osy z) je zanedbatelná. Díky aplikovaným okrajovým podmínkám je elektrické pole nenulové pouze ve směru osy z, zatímco magnetické pole má složky pouze ve směru os x a y. Na hranách kovového flíčku platí Neumannova okrajová podmínka pro elektrické pole (∂E/∂n = 0, kde n je normála k hranám flíčku). Proto hrany kovového flíčku lze považovat za dokonale magnetické stěny (PMC – perfect magnetic conductor). Momentová metodaMomentová metoda je numerická metoda pro řešení integrálních rovnic (hledaná funkce, např. rozložení proudu na anténě, vystupuje v integrandu určitého integrálu). Podstata metody spočívá v diskretizaci struktury, ve formální aproximaci hledané funkce pomocí známých bázových funkcí (např. konstantní funkce na jednotlivých diskretizačních buňkách) a neznámých aproximačních koeficientů (hodnota konstantní funkce na jednotlivých buňkách), v dosazení aproximace do výchozího vztahu (neznámé aproximační konstanty vytkneme před integrál a integrujeme známé bázové funkce), v minimalizaci chyby aproximace (výchozí vztah s dosazenou formální aproximací postupně násobíme Diracovými impulsy ve středech jednotlivých diskretizačních buněk a integrujeme přes celou zkoumanou strukturu – dostáváme tak N rovnic pro N neznámých aproximačních koeficientů) a v řešení výsledné maticové rovnice (získáváme aproximační koeficienty a tedy i aproximaci řešení – hledané funkce v integradu integrální rovnice). Momentová metoda ve spektrální oblasti (kapitola 6)Předpokládejme, že kmitočtově selektivní povrch je nekonečně rozlehlý a že rozmístění vodivých elementů je periodické. Je-li takový selektivní povrch ozařován rovinnou vlnou, je potom rovněž rozložení indukovaných proudů na elementech je periodickou funkcí. Jelikož spektrum periodické funkce je diskrétní, spojitému rozložení proudů na vodivých elementech odpovídá diskrétní prostorové spektrum. Rovnice pro diskrétní spektra pak lze relativně snadno přepsat do maticové formy a získané maticové rovnice lze poté řešit na počítači. Momentová metoda ve spektrální oblasti, momentová metoda v prostorové oblasti (kapitola 4)Časoprostorové rozložení elektromagnetického pole je popsáno členem exp[j(ωt-kr)], kde ω je úhlový kmitočet (změna fáze za jednu sekundu), t značí čas, k je vlnové číslo (změna fáze na jednom metru v daném směru, tedy prostorový kmitočet) a r značí vzdálenost (v daném směru). Analýza v prostorové oblasti je založena na výpočtech pro jedinou hodnotu prostorového kmitočtu k (vzdálenost r je proměnná). U analýzy ve spektrální oblasti je tomu naopak – vzdálenost r bereme jako fixní a výpočet provádíme pro všechny možné prostorové kmitočty k. Momentová tabulkaTermínem momentová tabulka označujeme matici, která obsahuje vzájemné příspěvky mezi jednotlivými nábojovými a proudovými buňkami Nehomogenní vlnová rovniceTermínem homogenní vlnová rovnice označujeme rovnici
Uvedená rovnice platí v kartézském souřadném systému. Pokud vektor E vyhovuje uvedené rovnici, potom tento vektor popisuje šíření vlny. Je-li pravá strana rovnice nulová, jsme daleko od zdrojů a zdrojem vlnění je vlnění samo. Nehomogenní vlnová rovnice má na rozdíl od (1) nenulovou pravou stranu
Na pravé straně (2) vystupuje časová derivace (jω) zdrojového proudu Je. Tato rovnice se musí používat v blízkosti zdrojů vlnění (antén). Nábojová buňkaNábojová buňka je posunuta o polovinu segmentu vzhledem k buňce proudové. Střed nábojové buňky tak leží na hraně buňky proudové. Tento střed odpovídá bodu, v němž počítáme hodnotu náboje. Obecná teorie difrakceObecná teorie difrakce se zabývá výpočtem ohybu vlnění na překážkách obecného tvaru. Jelikož se jedná o nesmírně obtížný úkol, v praxi využíváme výsledků pro relativně jednoduché geometrické struktury (např. pro rotační elipsoid) a reálná tělesa se snažíme těmto objektům přiblížit (např. úsek vodiče můžeme považovat za extrémně protáhlý elipsoid). Odraz vlnyK odrazu vlny dochází při dopadu vlnění na dostatečně rozlehlé a dokonale hladké rovinné rozhraní mezi dvěma prostředími s různými elektrickými parametry. OhniskoTermínem ohnisko označujeme místo, v němž se protínají paprsky. Okrajové podmínkyOkrajové podmínky jsou podmínky, které musí splňovat elektromagnetické pole na rozhraní dvou různých prostředí. Pro složky intenzity E tečné k rozhraní platí Eteč 1 = Eteč 2. Obě intenzity jsou intenzity v bodech těsně přilehlých k rozhraní, ale po jeho různých stranách. Pro normálové složky elektrické indukce platí obdobně Dnorm 1 = Dnorm 2. Pro magnetické pole platí analogicky rovnost tečných složek intenzity H a normálových složek indukce B. Ve zvláštním případě, kdy jedno prostředí je dokonale vodivé pro elektrické proudy nebo pro magnetické proudy, můžeme okrajové podmínky rozdělit na podmínku Dirichletovu a podmínku Neumannovu. Dirichletova podmínka říká, že ta složka vektoru elektrické (magnetické) intenzity, která je tečná k dokonalému elektrickému (magnetickému) vodiči, musí být na tomto vodiči nulová
Neumannova podmínka říká, že derivace (změna) vektoru elektrické (magnetické) intenzity ve směru normály k dokonalému magnetickému (elektrickému) vodiči musí být na tomto vodiči nulová.
Zkratkou PEC značíme dokonalý elektrický vodič (Perfect Electric Conductor), zkratkou PMC dokonalý vodič magnetický (Perfect Magnetic Conductor). Symbol n značí normálu k vodivému povrchu. PaprsekPaprsek je křivka, jejíž tečna má v každém bodě směr gradientu eikonály. Paprsek má v každém bodě směr nejstrměji se měnící fáze a je to i směr Poyntingova vektoru, tedy směr toku energie. Paraxiální vlnyParaxiální vlny jsou vlny, jejichž směry šíření jsou téměř stejné (jejich paprsky svírají vzájemně malé úhly). O paraxiálních vlnách hovoříme většinou tehdy, když jejich soubor (součet) má nějaký zvláštní význam. Např. jedinou neuniformní rovinnou vlnu šířící se ve směru osy z můžeme vyjádřit součtem paraxiálních uniformních rovinných vln, šířících se ve směrech nepatrně odchýlených od osy z. PhononJedná se o kvazičástici, která byla zavedena, aby reprezentovala kvantum vibrační energie krystalické mřížky. Pomocí těchto částic popisujeme šíření zvukových (mechanických) vln v krystalech. Planární mikrovlnné vedeníPlanárním mikrovlnným vedením budeme obecně rozumět strukturu, sestávající z kovové rovinné zemní desky a z jednoho nebo více s ní rovnoběžných planárních vodičů (z kovových pásků jako elektrických vodičů nebo ze štěrbin v kovové desce jako vodičů magnetických). Popsaná struktura může být dále doplněna různými dielektrickými vrstvami, které se mohou vzájemně lišit svými elektrickými a magnetickými vlastnostmi. Planární vedení může být buď otevřené (open, to jsme právě popsali) nebo stíněné (shielded), tj. umístěné dovnitř kovového obdélníkového vlnovodu. Podélně homogenní vlnovodTermín podélně homogenní vlnovod nám říká, že vlastnosti vlnovodu jsou v podélném směru neměnné. Je-li vlnovod bezeztrátový, mění se v podélném směru pouze fáze vlnění – jeho amplituda zůstává konstantní. Polarizace dielektrikaDielektrikum neobsahuje volné nosiče náboje. Dielektrikum sestává z atomů, u nichž je kladný náboj jádra roven zápornému náboji elektronů. Pokud vložíme dielektrikum do vnějšího elektrického pole, je jádro s kladným nábojem vychýleno proti směru vnější elektrické intenzity a elektrony se záporným nábojem jsou vychýleny ve směru vnější intenzity. V dielektriku tak vzniká vnitřní elektrické pole, jehož intenzita má opačnou orientaci nežli je tomu u pole vnějšího. Vnější elektrické pole je tedy uvnitř dielektrika zeslabováno. Polarizace vlnPolarizace popisuje, jak je u vlnění orientován vektor intenzity elektrického pole. Při šíření vlny ve volném prostředí může existovat polarizace lineární nebo eliptická. Vlna je lineárně polarizovaná, když vektor E má během celé periody stále stejný směr. Znázorníme-li vektor okamžité hodnoty intenzity šipkou, pak její délka se mění během půlperiody od nuly do maxima a zpět, během druhé půlperiody se opakuje totéž s opačnou orientací. Koncový bod se pohybuje po úsečce. Je-li vlna elipticky polarizovaná, její vektor intenzity elektrického pole během periody mění svůj směr. Šipka, znázorňující okamžitou hodnotu intenzity pole se během periody otáčí a současně mění svou délku tak, že její koncový bod se pohybuje po elipse. Tu oběhne právě za jednu periodu. Ve zvláštním případě může se koncový bod pohybovat po kružnici (kruhová polarizace). Eliptická (kruhová) polarizace může být pravotočivá nebo levotočivá. Smysl otáčení se posuzuje při pohledu ve směru šíření. Elipticky polarizovanou vlnu lze považovat za superpozici dvou koherentních lineárně polarizovaných vln, jejichž vektory E kmitají v různých směrech a s určitým nenulovým vzájemným posuvem. Při šíření vlny v blízkosti roviny rozhraní dvou prostředí rozlišujeme polarizaci kolmou a polarizaci rovnoběžnou. Nejprve definujme rovinu dopadu: to je rovina kolmá k rovině rozhraní a současně rovnoběžná se směrem šíření vlny. Kolmo polarizovaná vlna má vektor E kolmý na rovinu dopadu, rovnoběžně polarizovaná vlna má vektor E rovnoběžný s rovinou dopadu. Je-li rovinou rozhraní rovina zemského povrchu, pak se často pro kolmo polarizovanou vlnu používá termín vlna horizontálně polarizovaná, pro vlnu rovnoběžně polarizovanou vlnu termín vlna vertikálně polarizovaná. Poměr stojatých vlnPoměr stojatých vln (PSV) kvantifikuje stojaté vlnění. PSV je pro bezeztrátové vedení (prostředí) konstantní a je definován jako poměr amplitudy napětí (proudu) stojaté vlny v kmitně k amplitudě napětí (proudu) v uzlu. Pro vedení (prostředí) ztrátové počítáme PSV v určitém místě z hodnoty činitele odrazu ρ v tomtéž místě
Postupné vlněníPokud se vlnění šíří nekonečně rozlehlým a zcela volným prostředím, šíří se jako postupné vlnění. Fáze kmitání se ve směru šíření rovnoměrně zpožďuje o k' radiánů na každý metr vzdálenosti a amplituda vlnění je buď konstantní (v bezeztrátovém prostředí) nebo monotónně klesá (ve ztrátovém prostředí). Povrchová vlnaPovrchové vlny jsou vlny vedené rozhraním mezi dvěma prostředími. Šíří se podél tohoto rozhraní. S povrchovými vlnami se můžeme setkat např. na rozhraní vzduchu a zemského povrchu nebo u mikropáskových vedení (dielektrický substrát, jehož rubová strana je zcela pokovena a na jehož lícní straně se nachází relativně úzký pásek). Jedná se o vlnění, které se nešíří podél páskového vodiče ale rozhraním dielektrikum – vzduch. Amplituda tohoto vlnění ve směru kolmém na rozhraní exponenciálně klesá. Poyntingův vektorPoyntingův vektor matematicky vypočteme jako vektorový součin vektoru elektrické intenzity a komplexně sdruženého vektoru intenzity magnetické. Směr Poyntingova vektoru je totožný se směrem šíření energie, velikost Poyntingova vektoru je ve většině situací rovna plošné hustotě výkonu [W/m], přenášeného vlněním. Poytingův vektorPoytingův vektor matematicky vypočteme jako vektorový součin vektoru elektrické intenzity a komplexně sdruženého vektoru intenzity magnetické. Směr Poytingova vektoru je totožný se směrem šíření energie, velikost Poytingova vektoru je ve většině případů rovna plošné hustotě výkonu [W/m] přenášeného vedením. Počítání s malými číslyPředpokládejme, že máme velmi malou skalární hodnotu x<<1. Potom pro toto číslo platí následující přibližné vztahy:
konkrétně např.
Besselovy funkce:
Neumannovy funkce:
Princip dualityPohledem na Maxwellovy rovnice
se snadno se přesvědčíme o tom, že záměnami
přejde levá soustava rovnic v pravou a naopak. Stejnými záměnami lze však získat i výsledek řešení třeba pravé soustavy z výsledku řešení levé soustavy při stejných okrajových podmínkách. Mějme např. dvě podobné úlohy, které se liší jenom tím, že v první je pole buzeno elektrickými proudy a v druhé proudy magnetickými. Řešení první úlohy tedy vychází z levé dvojice rovnic (1), (2), řešení druhé úlohy z pravé dvojice. Řešení první úlohy známe, druhá úloha nám dělá potíže. To však nevadí. Podle principu duality získáme hledané řešení druhé úlohy pouhou záměnou (3) ve výsledku úlohy první. Podmínky pro aplikaci principu duality jsou splněny u komplementárních útvarů. Dva komplementární útvary jsou dva rovinné útvary. U jednoho je část roviny vodivá (plech), zbývající část je nevodivá (prázdná, vzduch). U druhého útvaru je to přesně obráceně. Např. k úzkému pásku plechu je komplementární úzká štěrbina ve velké vodivé desce; pásek a štěrbina musí mít stejné rozměry. V pásku lze vybudit elektrický proud a pak září jako dipól. Ve štěrbině lze vybudit magnetický proud. Vzorec pro vyzařování štěrbiny lze získat ze vzorce pro záření dipólu záměnami (3). Princip zrcadleníPrincip zrcadlení umožňuje snadno postihnout vliv dobře vodivých rovinných ploch v blízkosti antény na její záření. Záření antény totiž indukuje na ploše proudy, které k záření antény také přispívají. Podle principu zrcadlení je příspěvek indukovaných proudů shodný se zářením zrcadlových obrazů elementů skutečné antény. Vertikální element se zrcadlí s proudem shodným co do amplitudy i fáze. Horizontální element má v zrcadlovém obrazu proud s opačnou fází. Program WinMIDEPříklady k deváté kapitole jsou připraveny v programu WinMIDE. Abyste je mohli opravdu využít, potřebujete si tento program nainstalovat. Uveďme si nyní základní informace o tomto programu. Licenční podmínkyVerze WinMIDE, která k Vám přichází s multimediální učebnicí, nesmí být využívána ke komerčním účelům. Nesmí také být šířena mimo tuto učebnici. Není povoleno její modifikování. Na její správnou funkci není autory poskytována žádná záruka. UrčeníProgram WinMIDE je určen k analýze a optimalizaci lineárních vf. a mikrovlnných obvodů. Tyto obvody mohou být složeny z prakticky libovolného počtu prvků. Knihovna programu obsahuje vedení, vázaná vedení a další prvky, ze kterých lze sestavit řadu obvodů. Prvky, které nejsou v knihovně přímo obsaženy, lze zadat prostřednictvím vzorce (je-li znám), nebo pomocí souboru obsahujícího (změřené) parametry obvodu. Uživatelské rozhraní je vytvořeno tak, aby bylo program možno snadno ovládat. Obsahuje grafický editor obvodů (schemat). Výstupem analýzy mohou být rozptylové parametry obvodu (přenosy a odrazy) a činitel stability. Optimalizovat lze vzhledem k libovolné kombinaci požadovaných rozptylových parametrů či činitelů stability. Součástí instalace WinMIDE jsou i dva pomocné programy - Interaktivní Smithův diagram (slouží mj. k automatizovanému návrhu přizpůsobovacích obvodů) a program pro analýzu a syntézu základních mikrovlnných vedení. Požadavky na vybavení počítačePC, monitor s rozlišením alespoň 800x600, operační systém Microsoft Windows 98, Windows ME, Windows NT SP6, Windows 2000 SP2. Doporučuje se alespoň 128 MB paměti. Volné místo na disku: 10 MB. Omezení verze přicházející s učebnicíVerze programu obsažená v učebnici umožňuje optimalizovat nejvýše čtyři proměnné. Krom toho knihovna demoverze neobsahuje diskontinuity na vedeních. Demoverze plně postačuje k probrání všech příkladů, dodaných s touto multimediální učebnicí. Stejně tak postačuje k samostatnému procvičení látky. Jak instalovat programNejprve je třeba získat instalační soubory. Aktuální verzi programu naleznete na http://www.mide.cz/ucebnice/images/WinMIDE.exe ve formě samorozbalovacího archivu. Spusťte instalační program, který Vás provede instalací. V případě, že se při instalaci WinMIDE na Váš počítač vyskytnou problémy, kontaktujte support@mide.cz. Prostorová perioda, prostorová frekvence (kapitola 6)Tak jako jsme v časové oblasti označovali termínem perioda nejmenší časovou vzdálenost (časový interval, [s]) dvou okamžiků, v nichž se fáze harmonického kmitání liší o 2π (je zdánlivě stejná), tak analogicky v prostorové oblasti označujeme vzdálenost [m] dvou míst, v nichž se fáze vlnění liší o 2π (a je tedy zdánlivě stejná) jako prostorovou periodu.
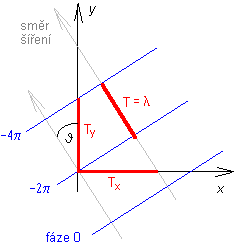
Na obrázku je naznačeno šíření rovinné vlny šikmo doleva nahoru a jsou v něm zakresleny tři rovinné vlnoplochy kolmé na směr šíření. Symbolem T je okótována prostorová perioda ve směru šíření, symboly Tx a Ty označují prostorové periody ve směrech zvolených souřadných os x a y. prostorová perioda má rozměr [metr] a prostorová perioda ve směru šíření je rovna vlnové délce λ. Převrácená hodnota prostorové periody je prostorová frekvence: f = 1/T, fx = 1/Tx a fy = 1/Ty (ve směru šíření, ve směru x a ve směru y). Má rozměr 1/m. Z obrázku se snadno přesvědčíme, že 2πf = ω = 2π/T = 2π/λ = k (vlnové číslo ve směru šíření) a podobně např. 2πfy = ωy = ky (vlnové číslo ve směru y). Protože ky = k cos(ϑ), je prostorová frekvence závislá na směru šíření. Prostorová perioda, prostorová frekvence (kapitola 7)Termíny prostorová perioda a prostorová frekvence se vztahují k elementárnímu optickému signálu. Tak jako jsme v časové oblasti označovali termínem perioda nejmenší časovou vzdálenost [sekunda] dvou okamžiků, v němž má signál stejnou fázi, analogicky v prostorové oblasti označujeme vzdálenost [metr] dvou míst stejnou fází jako prostorovou periodu. Prostorová frekvence je pak obrácenou hodnotou prostorové periody. Vzhledem k tomu, že prostorový signál je dvojrozměrný, máme i dvě prostorové periody (Tx ve směru x a Ty ve směru y) a dvě prostorové frekvence (fx = 1/Tx a fy = 1/Ty). Prostorový signál, optický signál, elementární prostorový signálProstorový signál (nebo také optický signál) je přenášen elektromagnetickým vlněním. Informace není obsažena v časové závislosti intenzity pole , nýbrž v rozložení amplitudy intenzity pole v rovině kolmé na směr šíření: E = E(x,y) když z je směr šíření. Elementární prostorový signál má rozložení amplitudy v jednom směru (např. x) harmonické, v druhém směru konstantní. Proudová buňkaProudová buňka je totožná s diskretizační buňkou při analýze mikropáskových antén (flíčků, dipólu) momentovou metodou. Nad plochou proudové buňky jsme vždy předpokládali konstantní hodnotu proudu. Příčně elektromagnetická vlnaTermínem příčně elektromagnetická vlna označujeme vlnu, u níž jsou jak vektor intenzity elektrického pole tak vektor intenzity pole magnetického kolmé na směr šíření. S takovou vlnou se setkáváme např. u koaxiálního vedení (vektory intenzity elektrického pole jsou směrovány radiálně od vnitřního vodiče k vodiči vnějšímu, siločáry magnetického pole tvoří soustředné prstence mezi vnitřním a vnějším vodičem). Obecně můžeme říci, že příčně elektromagnetické vlny se šíří po vedeních, která sestávají ze dvou nebo více vodičů, jež jsou umístěny v homogenním prostředí. Mikropáskové vedení je sice vedením dvouvodičovým (mikropásek a zemní deska), avšak není splněna podmínka homogenního prostředí (substrát má jiné elektrické parametry než vakuum nad páskem). Jelikož při šíření příčně elektromagnetické vlny by nebyly splněny podmínky na rozhraní dvou dielektrik, musí mít pole vždy podélnou složku. RadomAnglickým slovem radom označujeme anténní kryt, který má za úkol chránit anténu před vlivem prostředí (déšť, hmyz, ptáci, atd.). Anténní kryt by měl rovněž tvořit vhodné rozhraní, které umožní dosáhnout požadovaných parametrů antény (měl by způsobovat minimální ztráty při prostupu vlny, neměl by jakkoli degradovat parametry chráněné antény, atd.). Rayleighova vzdálenostRayleighova vzdálenost je vzdálenost, od níž se vlna nešíří ve směrech odpovídajících rovnoběžným paprskům, ale ve směrech, které odpovídají paprskům rozbíhavým. Reflektorová anténaReflektorové antény sestávají z tzv. primárního zářiče (např. dipól) a z reflektoru (např. paraboloid). Dopadá-li na paraboloid rovinná vlna, parabolický reflektor soustřeďuje veškerou zachycenou energii do svého ohniska. Je-li v ohnisku umístěna primární anténa, je výsledkem velmi silný signál na jejím výstupu. Reziduum, metoda vážených reziduí, váhová funkcePokud dosadíme do řešené rovnice aproximaci tohoto řešení a ne řešení přesné, nebude řešená rovnice splněna zcela přesně. Tuto skutečnost respektujeme přičtením zbytkové funkce (rezidua) k pravé straně rovnice s dosazenou aproximací. Abychom zbytkovou funkci minimalizovali (tj. abychom dostali co možná nejpřesnější aproximaci), násobíme zbytkovou funkci funkcí váhovou, integrujeme přes celou oblast řešení a výsledek položíme roven nule. Tento postup nazýváme metodou vážených reziduí. Rezonanční odporTermínem rezonanční odpor značíme vstupní odpor flíčkové antény, která je právě v rezonanci (délka flíčku je rovna polovině vlnové délky). Hodnotu rezonančního odporu můžeme ovlivňovat volbou šířky flíčku a změnou pozice vstupu antény (v případě mikropáskového napájení vnořujeme napájecí mikropásek do flíčku). Rovina E, rovina HRovinou H nazýváme rovinu, v níž leží siločáry magnetického pole, vyzařovaného anténou. V případě dipólu to je rovina, která je na dipól kolmá. Rovinou E nazýváme rovinu, v níž leží siločáry pole elektrického. U dipólu se jedná o všechny roviny, v nichž leží samotný dipól. Rovina dopaduRovina dopadu je kolmá na rovinu rozhraní a je rovnoběžná se směrem šíření dopadající vlny. Rovina rozhraníRovinou rozhraní rozumíme rovinu, která odděluje dvě prostředí s různými elektrickými a magnetickými parametry. Rovinná vlna (kapitola 2,3,4)Rovinná vlna je charakteristická rovinnou vlnoplochou (spojením míst se stejnou fází dostaneme rovinu). Za rovinnou vlnu můžeme považovat vlnu ve velmi velké vzdálenosti od zdroje, pokud ji pozorujeme jen v malé části prostoru (v rámci velké oblasti je vlna vždy vlnou kulovou). Rovinná vlna (kapitola 6)Rovinná vlna je charakteristická rovinnou vlnoplochou (tj. místa se stejnou fází tvoří rovinu). S rovinnou vlnou se můžeme setkat ve velké vzdálenosti od zdroje vlnění. Je-li zdrojem bodový zářič, jsou vlnoplochy vyzařovaného vlnění kulové. S rostoucí vzdáleností se však zakřivení vlnoplochy zmenšuje, takže ve velké vzdálenosti můžeme toto zakřivení zanedbat a s původně kulovou vlnou můžeme pracovat jako s vlnou rovinnou. Rovnice kontinuityRovnice kontinuity popisuje vzájemný vztah mezi změnou náboje v uzavřeném objemu a mezi proudy, které z tohoto objemu vytékají
Výtok proudu (divergence vektoru proudové hustoty) je roven poklesu (proto záporné znaménko) objemové hustoty náboje za jednotku času. Rozložení proudu, kmitna, uzelProud, který vtéká do dipólu, se na jeho koncích odráží a vrací se zpět do generátoru. Vtékající a odražený proud se na anténě sčítají. V místech, kde se tyto proudy setkají se stejnou fází, se objeví maximální amplituda proudu (mluvíme o kmitně stojatého vlnění). V místech, kde se proudy setkají s opačnou fází, bude amplituda proudu minimální (mluvíme o uzlu stojatého vlnění). Průběh amplitudy proudu na anténě nazýváme rozložením proudu (proudovou distribucí). Rozptyl vlněníNení-li rozhraní dokonale hladké (je drsné), pak se dopadající vlnění “odráží” v různých místech do různých směrů a odražená vlna v pravém slova smyslu nevzniká. Takový jev se nazývá rozptyl a vlnění vznikající na drsném rozhraní je vlnění rozptýlené. Jako rozptyl se také označuje vznik nového vlnění na velikém počtu náhodně situovaných částic nebo plošek, které jsou současně ozářeny nějakou dopadající (šířící se) vlnou. Příkladem je rozptyl vlnění na velikém souboru dešťových kapek za deště. Rozptylová maticeOznačíme-li napěťovou vlnu vstupující do dvojbranu branou 1 (2) a1 (a2) a vlny vystupující obdobně b1 a b2, lze pak v případě dvojbranu psát maticově jako Tato rovnice dává do souvislosti ekvivalentní napěťové vlny vstupující do dvojbranu a vlny z něho vystupující. Vztah je zprostředkován normovanou rozptylovou maticí. Při návrhu mikrovlnných obvodů je zvykem používat právě parametry, zvané rozptylové (Scattering parameters). Sférický souřadný systémJe tvořen dvěma křivočarými bázovými vektory φ0, ϑ0 a jedním přímočarým bázovým vektorem r0. Bázové vektory jsou vzájemně kolmé (viz obrázek). Libovolný bod je v tomto souřadném systému popsán vektorem
Diferenciální operátory jsou popsány následujícími vztahy:
Simplexní souřadniceV případě trojúhelníkových konečných prvků mají simplexní souřadnicové osy směr výšek trojúhelníka. Simplexní souřadnice nabývají hodnoty 1 ve vrcholu trojúhelníku a hodnoty 0 na protilehlé straně trojúhelníka. Simplexní souřadnice nezávisejí na tvaru ani na velikosti trojúhelníkového prvku, a proto lze všechny potřebné výpočty provést v simplexních souřadnicích pouze pro jediný konečný prvek a získané výsledky pak přepočíst pro konečné prvky ostatní. Co se týká fyzikální podstaty simplexních souřadnic, obecný bod P na ploše trojúhelníkového prvku rozděluje tuto plochu na tři dílčí trojúhelníky. Podíl obsahu dílčího trojúhelníka, ležícího proti prvnímu uzlu, k obsahu celého trojúhelníkového konečného prvku, udává souřadnici bodu P na první simplexní souřadné ose, přičemž se zbývajícími simplexními souřadnými osami je to podobné. Je tudíž zřejmé, že součet všech tří simplexních souřadnic v libovolném bodě trojúhelníkového konečného prvku musí být roven jedné. Skalární Greenova funkceSkalární Greenova funkce je funkcí úměrnosti mezi nábojovou hustotou ρ a mezi skalárním potenciálem V. Skalární potenciálSkalární potenciál usnadňuje zkoumání vlivu nepohybujících se nábojů (časové derivace se rovnají nule). Pole je pak popsáno první a třetí Maxwellovou rovnicí ve tvaru
Jelikož rotace gradientu je identicky rovna nule, bude (1) vždy splněna, položíme-li
(φ je zmíněný skalární potenciál). Nám pak postačí řešit jedinou skalární rovnici, rovnici Laplaceovu
Vztah (3) platí všude tam, kde je potenciál konečný a spojitý. Díky (3) máme pole popsáno jedinou parciální diferenciální rovnicí pro skalární funkci φ. Potenciál φ má i svůj fyzikální význam, vyplývající ze vztahu (2)
Jelikož součin E.dr je roven práci, kterou by pole vykonalo při přesunu jednotkového náboje po elementární dráze dr, udává nám elementární potenciál dφ úbytek (proto záporné znaménko) potenciální energie tohoto jednotkového náboje v našem elektrostatickém poli. Skládaný dipólSkládaný dipól sestává ze symetrického dipólu a z blízkého vodiče, který je s dipólem rovnoběžný a stejně dlouhý. Konce dipólu jsou spojeny s konci paralelního vodiče. Střed paralelního vodiče (bod naproti napájecí štěrbině) má nulový potenciál. Skládaný dipól se vyznačuje větší šířkou pásma a větší vstupní impedancí ve srovnání s obyčejným symetrickým dipólem. Smithův diagramSmithův diagram získáme vykreslením křivek, spojujících stejné hodnoty odporu a stejné hodnoty reaktance, do fázorové roviny činitele odrazu. Jeho kouzlo spočívá v tom, že umožňuje transformovat impedanci z konce vedení na jeho vstup, aniž bychom museli cokoli počítat. Stačí nám:
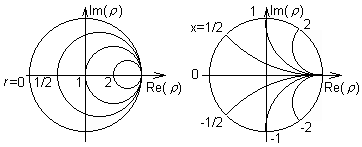
Směrová charakteristika anténySměrová charakteristika (směrový diagram) je grafickým vyjádřením směrových vlastností antény. Směrové vlastnosti přitom vyjadřujeme ve formě absolutní hodnoty podílu elektrické intenzity vyzařovaného vlnění v daném směru a nejvyšší hodnoty intenzity vyzařovaného vlnění (vše počítáme pro velmi velkou vzdálenost od antény). Směrová charakteristika se většinou vykresluje pro určitou rovinu (např. pro rovinu kolmou k dipólu nebo pro rovinu, v níž dipól leží). Snellův zákonSnellův zákon popisuje vztah mezi úhlem θ1, pod nímž dopadá vlna na rovinné rozhraní dvou dielektrik, a mezi úhlem θ2, který svírá směr šíření vlny s normálou k rozhraní v druhém prostředí (viz obrázek). Je-li index lomu prvého prostředí n1 (to vlna opouští) a index prostředí druhého n2 (do něho vlna vstupuje), jsou úhly svázány vztahem
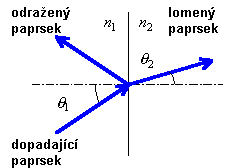
Součtové větySoučtovými větami rozumíme vztahy pro sinus a kosinus součtu (rozdílu) argumentů:
Spektrální funkce, Fourierova transformace, zpětná Fourierova transformaceSpektrální funkce vyjadřuje kmitočtovou závislost fázorů (komplexních amplitud) spektrálních složek signálu. Spektrální funkci S(ω) můžeme vypočítat ze známého časového průběhu signálu (např. U(t)) pomocí Fourierovy transformace:
Naopak, ze známé spektrální funkce můžeme určit časový průběh signálu pomocí zpětné Fourierovy transformace
Ve výše uvedených vztazích značí S(ω) spektrální funkci, U(t) je časový průběh signálu, ω je úhlový kmitočet a t značí čas. Stojaté vlněníJestliže se prostorem šíří alespoň dvě koherentní vlny různými směry, pak spolu interferují: v některých místech jsou jejich fáze trvale stejné, jejich intenzity se přímo sčítají a výsledná intenzita pole je velká. V jiných místech fáze stejné nejsou a součet intenzit je menší. Výsledná intenzita pole je tedy v různých místech různá, ale nemění se monotónně jako u postupné vlny, a ani fáze výsledného kmitání se nemění rovnoměrně. V prostoru vzniklo stojaté vlnění. V místech, kde je amplituda výsledného kmitání největší, jsou kmitny, v místech, kde je kmitání nejmenší, jsou uzly. Se stojatým vlněním se nejčastěji setkáváme tam, kde dochází k odrazu vlnění (v nehomogenním prostředí nebo na vedení). Vlna přímá interferuje s vlnou odraženou. Jejich směry šíření se liší o 180 stupňů. Sudý vid, lichý vidVid nebo mod je označením pro možné rozložení elektromagnetického pole v dané struktuře (vedení, rezonátoru). Z hlediska konstruktéra jsou pro každý vid důležité především dva následující parametry: konstanta šíření (útlum a fázový posun) a charakteristická impedance .Z hlediska kapitoly 7 mají zvláštní význam vidy sudé a liché. Tyto vidy vznikají na vedení tvořeném (alespoň) třemi galvanicky oddělenými vodiči, z nichž jeden tvoří společnou zem a dva vodiče jsou signálové. Uvedené pojmy předpokládají symetrické vedení, (velikosti napětí i proudů jsou na signálových vodičích stejné). Tato symetrie je dána zejména tehdy, pokud jsou rozměry a poloha obou vodičů vůči zemnímu vodiči stejné. Sudý vid (odd mode) se strukturou šíří, pokud jsou oba signálové vodiče napájeny soufázově. Lichý vid (even mode) se šíří, pokud jsou oba signálové vodiče buzeny v protifázi. U vedení s vlnou TEM mají oba vidy stejnou vlnovou délku (reálné části konstanty šíření jsou shodné). Světlost trasyUvažujme radiokomunikační spoj, sestávající z vysílače V a z přijímače P. V reálném terénu se mezi vysílačem a přijímačem mohou nacházet různé překážky (kopce, budovy), které ovlivňují kvalitu spoje. Světlostí trasy označujeme vzdálenost mezi vrcholem překážky a spojnicí vysílač – přijímač. Symetrický dipólSymetrickým dipólem rozumíme anténu, která sestává ze dvou stejně dlouhých lineárních ramen se společnou osou. Ramena jsou od sebe oddělena úzkou štěrbinou, do níž umisťujeme symetrický napěťový zdroj. Tvarová funkce, bázová funkce (kapitola 3)Termínem tvarová funkce označujeme dílčí aproximační funkci nad konečným prvkem, která v jednom uzlu konečného prvku nabývá jednotkové hodnoty a ve všech ostatních uzlech hodnoty nulové. Mezi nejčastěji používané tvarové funkce patří funkce lineární (rovina, která nabývá v jenom uzlu jednotkové hodnoty a která se svažuje do nuly v ostatních uzlech) a funkce kvadratická (funkce je opět v jednom uzlu jednotková a v ostatních uzlech nabývá nulové hodnoty). Všechny tvarové funkce, které nabývají jednotkové hodnoty ve stejném uzlu, pak společně tvoří funkci bázovou (basis function). V případě dvourozměrných lineárních funkcí má bázová funkce tvar jehlanu v jednotkovou hodnotou ve vrcholu a s nulovou hodnotou na hranách všech konečných prvků, které sdílejí společný uzel s jednotkovou hodnotou. Uniformní rovinná vlna, neuniformní rovinná vlnaTermínem uniformní rovinná vlna označujeme vlnu, která má na vlnoploše (v našem případě je vlnoplochou rovina) nejen stejnou fázi, ale i stejnou amplitudu vlnění. Naproti tomu u neuniformní rovinné vlny se velikost amplitudy vlnění na vlnoploše mění. Uzlová hodnotaUzlovou hodnotou rozumíme hodnotu hledané funkce v určitém, přesně definovaném bodě (uzlu). U po částech konstantní aproximace volíme uzly ve středech diskretizačních buněk. Uzlové konečné prvkyUzlové konečné prvky slouží k po částech spojité aproximaci rozložení skalární veličiny v analyzované struktuře. V nejjednodušším případě je skalární veličina nad plochou každého konečného prvku aproximována lineární funkcí. Tuto lineární aproximaci přitom skládáme ze tří dílčích lineárních funkcí, z nichž každá nabývá v jednom určitém vrcholu trojúhelníkového prvku jednotkové hodnoty a ve zbývajících dvou vrcholech hodnoty nulové. Násobíme-li dílčí lineární funkce hodnotou aproximované veličiny v tom vrcholu trojúhelníka (v tom uzlu), v němž nabývá funkce jednotky, a sečteme-li popsané součiny dostaneme lineární aproximaci veličiny E nad n-tým konečným prvkem E~(n). Ve výše uvedeném vztahu značí Em(n) uzlovou hodnotu veličiny E v m-tém uzlu (v m-tém vrcholu) n-tého trojúhelníkového prvku a Nm(n) je lineární funkce nabývající jednotkové hodnoty v m-tém uzlu n-tého prvku. U popsané uzlové aproximace mají uzlové hodnoty veličiny Em význam prostorových vzorků aproximované veličiny E. Vektorový potenciálVektorový potenciál A zavádíme tak, aby byla identicky splněna čtvrtá Maxwellova rovnice
Jelikož identicky rovna nule je divergence rotace, definujeme vektorový potenciál vztahem
Rozložení potenciálu A tedy jednoznačně určuje pole B. Naopak určitému poli B neodpovídá jediný potenciál A. Jestliže (1) platí pro nějaký vektor A, je potom tento vztah splněn i pro všechny možné vektory A’=A + grad ψ , kde ψ je libovolná skalární funkce. Rotace gradientu je totiž identicky rovna nule. Popsané nejednoznačnosti se zbavíme, pokud formulujeme pro A nějakou dodatečnou podmínku. Zavedení této dodatečné podmínky je nazýváno kalibrací potenciálu. Zmiňme se ještě o fyzikálním významu potenciál A.Ten vyplývá z definičního vztahu pro magnetický indukční tok plochou S
Na základě uvedeného vztahu můžeme říci, že magnetický indukční tok plochou S je roven cirkulaci vektorového potenciálu po okrajové křivce této plochy. Vid vlny, vidová čísla, dominantní vid, pásmo jednovidovostiVlny, které se šíří ve vlnovodu, jsou charakterizovány určitým příčným rozložením pole. O vlně s určitým příčným rozložením pole mluvíme jako o určitém vidu (módu) vlny. Každý vid je charakterizován určitým kritickým kmitočtem, určitou fázovou rychlostí, délkou vlny a rychlostí skupinovou. Vid s nejnižším kritickým kmitočtem nazýváme dominantním videm. Pásmo kmitočtů, pro něž se vlnovodem šíří jediný vid vlny, nazýváme pásmem jednovidovosti. Každý vid bývá charakterizován určitými celočíselnými konstantami. Tyto konstanty nazýváme vidovými čísly. V případě obdélníkového vlnovodu nám vlnová čísla říkají, kolik půlvln stojatého vedení je naskládáno ve směrech příčných souřadnic. Např. u vidu TM11 (příčně magnetická vlna) má podélná složka vektoru intenzity elektrického pole jednu půlvlnu ve směru osy x a jednu půlvlnu ve směru osy y (je-li osa z totožná s osou vlnovodu). U vidu TE10 (příčně elektrická vlna, dominantní vid obdélníkového vlnovodu) je ve směru x jedna půlvlna podélné složky vektoru intenzity magnetického pole a ve směru y je tato složka konstantní (v tomto směru máme 0 půlvln stojaté vlny). Vlna kolmo polarizovanáVlna kolmo polarizovaná má vektor E kolmý na rovinu dopadu. Vlna rovnoběžně polarizovanáVlna rovnoběžně polarizovaná má vektor E rovnoběžný s rovinou dopadu. VlnoplochaVlnoplochou rozumíme plochu, na které má vlna konstantní fázi. Amplituda vlny může být na vlnoploše jak konstantní (mluvíme o uniformní vlně) tak proměnná (vlna neuniformní). VlnovodVlnovodem rozumíme dutou kovovou trubici, jejíž příčné rozměry jsou srovnatelné s délkou vlny přenášeného signálu. Vlnění se vlnovodem šíří v podélném směru způsobem, který je možno interpretovat jako postupné odrazy od stěn. V příčném směru vzniká stojatá vlna (v různých bodech příčného průřezu je obecně různá amplituda intenzity pole). Vlnová délkaVlnová délka je nejmenší možná vzdálenost dvou míst v prostoru, v němž má vlnění stejnou fázi. Vlnová rovniceVlnová rovnice je diferenciální rovnicí druhého řádu pro vektor intenzity elektrického nebo magnetického pole. Jestliže intenzity pole vlnové rovnici vyhovují, má pole charakter vlnění. Pro intenzitu harmonického elektrického pole má vlnová rovnice tvar
V rovnici je ∇ diferenciální operátor (v kartézských souřadnicích ∇f = [∂f/∂x; ∂f/∂y; ∂f/∂z]), E je vektor intenzity elektrického pole, k značí vlnové číslo, ω je úhlový kmitočet harmonické vlny, μ značí permeabilitu prostředí a Jvn je zdrojový (vnucený) proud, který vlnění budí. Pro intenzitu harmonického pole magnetického je vlnová rovnice tvaru obdobného. Homogenní vlnová rovnice má nulovou pravou stranu (tj. nevystupuje v ní zdrojový proud). Homogenní rovnicí můžeme popsat vlnění ve velké vzdálenosti od zdroje, v níž je již vliv zdroje zanedbatelný a v níž je vlna sama zdrojem dalšího vlnění. Vlnové metodyVlnové metody vycházejí z popisu elektromagnetického pole na vedení pomocí úplných, nezjednodušených Maxwellových rovnic. Platnost vlnových metod tedy není kmitočtově omezena. Na druhou stranu jsou vlnové metody založeny na numerických metodách (analytické řešení Maxwellových rovnic pro planární vedení neznáme), takže vyžadují vysoký výpočetní výkon. Vlnové číslo (kapitola 2,3,7)V bezeztrátovém prostředí vlnové číslo udává, o kolik radiánů se mění fáze šířící se vlny na každý metr vzdálenosti v určitém směru. Nejčastěji je to směr šíření vlny. Rozměr vlnového čísla je rad/m. Vlnové číslo bezprostředně souvisí s délkou vlny vztahem k = 2π/λ a fázovou rychlostí šíření k = ω/vf. Je-li vlnové číslo k vlnovým číslem ve směru šíření vlny, pak i vlnová délka a fázová rychlost jsou veličiny platné pro směr šíření. Pro jiný směr, než je směr šíření, platí uvedené vztahy beze změny, jen všechny tři veličiny nabývají hodnot platných pro onen jiný směr. Ve směru šíření je vlnové číslo největší, vlnová délka a fázová rychlost jsou nejmenší. Ve ztrátovém prostředí je vlnové číslo komplexní. Jeho reálná část k' udává změnu fáze vlnění na vzdálenosti jednoho metru, jak bylo vysvětleno výše. Záporně vzatá imaginární část k'' udává měrný útlum vlny. Pokles amplitudy vlnění na vzdálenosti r je
kde k'' je imaginární část vlnového čísla ve směru r. Vlnové číslo (kapitola 4)Vlnové číslo udává, o kolik radiánů se změní fáze vlny na jednom metru délky, tj. k = 2π/λ, kde λ je délka vlny v tom směru, v němž počítáme vlnové číslo. Délka vlny λ je nejkratší prostorovou vzdáleností dvou míst se stejnou fází. Jedná se tedy o prostorovou obdobu periody T, která udává nejkratší časovou vzdálenost dvou okamžiků, v nichž má vlna stejnou fázi. Porovnáme-li vztah pro úhlový kmitočet ω = 2π/T (udává, o kolik radiánů se změní fáze během jedné sekundy) se vztahem pro vlnové číslo, nalezneme u nich formální shodu. Proto můžeme vlnové číslo považovat za prostorový kmitočet. Vlnový vektor, vlnové číslo (kapitola 6)V bezeztrátovém prostředí vlnové číslo udává, o kolik radiánů se mění fáze šířící se vlny na každý metr vzdálenosti v určitém směru. Nejčastěji je to směr šíření vlny. Rozměr vlnového čísla je rad/m. Vlnové číslo bezprostředně souvisí s délkou vlny vztahem k = 2π/λ a fázovou rychlostí šíření k = ω/vf. Je-li vlnové číslo k vlnovým číslem ve směru šíření vlny, pak i vlnová délka a fázová rychlost jsou veličiny platné pro směr šíření. Pro jiný směr, než je směr šíření, platí uvedené vztahy beze změny, jen všechny tři veličiny nabývají hodnot platných pro onen jiný směr. Ve směru šíření je vlnové číslo největší, vlnová délka a fázová rychlost jsou nejmenší. Velikost vlnového vektoru je shodná s velikostí vlnového čísla. Směr vlnového vektoru je shodný se směrem šíření elektromagnetické vlny. Vypočteme-li průměty vlnového vektoru do různých směrů, můžeme z těchto průmětů snadno vypočíst délku vlny a fázovou rychlost v těchto směrech. Vrstevnatá prostředíTermínem vrstevnaté prostředí označujeme prostředí, sestávající z několika planparalelních vrstev s různými elektrickými vlastnostmi (s různou permitivitou). Pokud se takovým prostředím šíří rovinná vlna, na rozhraních jednotlivých vrstev dochází k částečným odrazům. Prostupující vlny se skládají s vlnami odraženými, takže v prostředí vzniká stojaté vlnění. Vstupní impedance antény, impedance zářeníVstupní impedance antény je impedance, kterou bychom naměřili na vstupních svorkách antény. Vstupní impedance sestává z odporu záření RΣ(vynásobíme-li jej kvadrátem vstupního proudu Ivst2, dostaneme činný vyzářený výkon), ze ztrátového odporu Rztr (Rztr Ivst2 udává výkon, který se v anténě a jejím okolí mění v teplo) a z reaktance záření XΣ (popisuje vzájemné přelévání energie mezi anténou a elektromagnetickým polem v jejím okolí). Odpor záření a reaktance záření tvoří dohromady impedanci záření. Vzdálená oblast, oblast zářeníVzdálenou oblastí rozumíme oblast vymezenou vzdáleností od antény a nekonečnem (d je největší příčný rozměr antény a λ značí vlnovou délku). Pro vzdálenou oblast můžeme použít představu, že dráhy vln z jednotlivých bodů antény do bodu příjmu jsou rovnoběžné. Válcová souřadná soustavaJe tvořena jedním křivočarým bázovým vektorem φ0 a dvěmi přímočarými bázovými vektory r0, z0. Bázové vektory jsou vzájemně kolmé (viz obrázek). Libovolný bod je v tomto souřadném systému popsán vektorem
Diferenciální operátory jsou ve válcovém souřadném systému popsány následujícími vztahy:
Válcová vlnaVálcová vlna je charakteristická válcovým tvarem vlnoplochy. Zdrojem válcové vlny může být např. nekonečně dlouhý vodič, protékaný střídavým proudem. Zisk antényZiskem antény rozumíme decibelové vyjádření maximální hodnoty činitele směrovosti
To je tzv. absolutní zisk. Relativní zisk udává, o kolik decibelů je maximální činitel směrovosti antény větší než činitel směrovosti nějaké referenční (vztažné) antény:
Za referenční anténu se často používá půlvlnný dipól. Činitel směrovosti D(φ,ϑ) popisuje směrovost vyzařování antény: činitel směrovosti je větší než jedna v těch směrech, do nichž zdroj záření soustřeďuje, a menší než jednička v těch směrech, v nichž je záření potlačováno. Činitel směrovosti všesměrového zdroje je pro všechny směry roven jedné. Znaménková konvenceČasoprostorové rozložení harmonického vlnění obvykle popisujeme členem exp(+jωt - jkr), kde úhlový kmitočet ω popisuje změnu fáze za jednotku času (t) a vlnové číslo k změnu fáze na jednotkové délce (r). Při posuvu časem se fáze zvětšuje, při posuvu prostorem ve směru šíření se zpožďuje. Pokud znaménka u sčítanců v exponenciální funkci přehodíme na exp(-jω t + jkr), na podstatě studovaných jevů se nic nezmění (zůstávají v platnosti všechny zákony). Nicméně je velmi důležité říci, kterou znaménkovou konvenci používáme, a je nezbytně nutné zvolenou konvenci uvažovat v celém výpočtu. Když potřebujeme nějaký matematický vztah převést z jedné konvence do druhé, stačí změnit znaménka u všech imaginárních jednotek (+j ↔ -j). Základní vid, parazitní vidyPři studiu šíření vln označujeme jako dominantní vid (základní vid) takový vid, který má nejmenší kritický kmitočet. Při studiu šíření vln přes periodické struktury (vln vyzařovaných z periodických struktur) označujeme jako základní ten vid, který má nejmenší prostorový kmitočet. Pod pojmem vid máme zde na mysli určitý směr vyzařovaného vlnění, v němž vlny, vycházející ze všech prvků struktury, přicházejí do místa pozorování se stejnou fází. Kdybychom přirovnali strukturu k anténní soustavě a prvky struktury odpovídaly prvkům této soustavy, pak základním videm by bylo vlnění, ve směru hlavního laloku soustavy. Nejmenší prostorový kmitočet má vlnění, šířící se ve směru, který je blízký směru normály ke struktuře (je-li shodný se směrem normály, je prostorový kmitočet roven nule). Stejně jako anténní soustava může mít kromě hlavního laloku (směřujícího kolmo nebo přibližně kolmo k ose řady) ještě stejně velký lalok směřující úplně jinam, tak i periodická struktura může intenzivně vyzařovat i v jiném směru, značně odchýleném od normály. Toto vyzařování je většinou nežádoucí (parazitní vid). Účinnost antény, účinnost vyzařování antényÚčinnost antény se definuje poměrem vyzařovaného výkonu ku příkonu. Pro účinnost můžeme odvodit jednoduchý vztah: (RΣvst je odpor záření, vztažený ke vstupnímu proudu, a Rztr je ztrátový odpor antény, vztažený ke vstupnímu proudu). Dobrá účinnost antény je podmíněna buď malým ztrátovým odporem a (nebo) velkým odporem záření. Naopak nízkou účinnost mají antény s malým odporem záření – a to jsou antény krátké proti délce vlny. Při výpočtu účinnosti vyzařování uvažujeme bezeztrátovou anténu (ztrátový odpor je nulový). Pak je účinnost vyzařování dána poměrem činného výkonu vyzářeného anténou (získá se integrací Poyntingova vektoru ve vzdálené oblasti přes celý poloprostor) a činného výkonu na napájecí svorce zářiče (antény). Činitel jakosti rezonátoruČinitel jakosti jakéhokoliv rezonančního obvodu s úhlovým kmitočtem ω0 je dán vztahem
kde W je energie elektromagnetického pole v obvodu a PZ značí ztracený výkon v obvodu. Činitel směrovostiČinitel směrovosti D(φ, ϑ) popisuje, do kterých směrů vyzařuje anténa větší výkon a do kterých výkon menší. U všesměrového zářiče je činitel směrovosti jednotkový pro všechny úhly φ a ϑ. U reálných antén nabývá činitel směrovosti hodnoty větší než jedna ve směrech, do nichž anténa záření soustřeďuje, a hodnoty menší než jednička v těch směrech, kam je záření potlačováno. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||