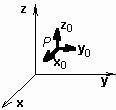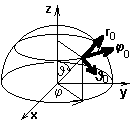RegisterAmpér lawAmpér law expresses the fact that the summation of induced conductive current Iind, of enforced conductive current Ivn and of displacement current dψ/dt, which pass the surface bounded by the closed curve l in the positive direction, equals to the circulation of the magnetic field intensity vector along this curve.
Circulation of vector A along the closed curve l can be imagined as a summation of scalar products of the vector A and a vector of elementary curve dl in the certain number of points on l. More points are considered, more accurate result is obtained. Antenna efficiency, efficiency of antenna radiationAntenna efficiency is defined as a ratio of a radiated power and a supplied one. Efficiency can be evaluated exploiting the following relation: (RΣvst is radiation resistance related to input current, and Rztr is lossy resistance related to input current). Good antenna efficiency is conditioned by a small lossy resistance and (or) by a high radiation resistance. On the contrary, low efficiency is exhibited by antennas of small radiation resistance, which is typical for antennas much shorter that the wavelength. Computing radiation efficiency, a lossles antenna is assumed (lossy resistance is zero). Then radiation efficiency is given as a ratio of a real power radiated by the antenna (we integrate Poynting vector in the far-field region over the whole half-space) and a real power at the input terminal of the antenna. Antenna gainAs the gain of the antenna, the maximum value of the directivity factor (in decibels) is understood
This gain is called the absolute one. The relative gain tells us, how much is the maximum directivity factor higher that the directivity factor of the reference antenna:
As the reference antenna, the half-wavelength long dipole is usually considered. Directivity factor D(φ, ϑ) describes the directivity of the antenna radiation: directivity factor is higher than one in those directions, where the radiation is concentrated, and is smaller than one in those directions, where the radiation is suppressed. Directivity factor of the isotropic source equals to one. Aperture-fed microstrip antennaMicrostrip antenna elements are excited via slots in the ground plane. The feeding transmission line is etched on a substrate, which is positioned below the substrate with the antenna. Both the substrates share the common ground plane with a slot. The transmission line can be found on the true side of the lower substrate. Basic mode, parasitic modesStudying wave propagation, the mode of the lowest critical frequency is called the dominant (basic) mode. Studying wave propagation through periodic structures, the mode of the lowest spatial frequency is called the basic mode. The term mode denotes here a certain direction of the radiated wave, for which waves radiated from all the parts of the antenna reach the observation point with the same phase. In analogy to the antenna array, the basic mode can be understood as a wave propagating in the main lobe direction. Wave propagating in the direction, which is nearly perpendicular to the structure, is of the lowest spatial frequency (for perpendicular direction, spatial frequency equals to zero). In analogy to the antenna array, even the periodic structure can have a side-lobe (an intensive radiation to another direction, significantly declining the normal). This radiation is usually undesired (parasitic mode). Basis functionBasis function forms a basis of approximating an unknown, sought function. Piecewise constant functions (functions are of unitary value over a single discretization element and are zero over the rest of elements) and piecewise linear functions are the most frequently used basis functions. BeamBeam is a curve, which tangent is of the same direction as the gradient of eiconale in every point. Beam is of the direction of the steepest phase variation and of the direction of Poynting vector, i.e. the direction of the energy flow. Bessel function, Neumann functionSolving wave equation in cylindrical and spherical coordinates by the method of variables separation, Bessel differential equation is obtained for a single variable (radial coordinate)
If n is not an integer number, linear combination of Bessel functions of order n and -n is the solution of the equation
If n = n is an integer number, solutions Jν(x) and J-ν(x) are linearly dependent and Neumann function Nn(x) has to be used as the second particular integral.
Biot-Savart lawThe force between electric charges in motion is called the magnetic force. The force field, which is created by a moving charge, is called the magnetic field. Magnetic field of the charge Q1, which moves by the velocity v 1, is quantified by magnetic displacement B. Magnetic displacement is given by Biot-Savart law Magnetic displacement tells us the force, which is caused by the charge Q1 moving by velocity v1 and which affects the unitary charge in r moving by unitary velocity. The symbol m0 denotes permeability of vacuum (m0= 1.26 * 10-6 H * m-1). Boundary conditionsBoundary conditions are met by the electromagnetic field on the boundary of two different media. For the component of E , which is tangential to the boundary, we write: Etang 1 = Etang 2. Both the intensities are measured in points, which are located near the boundary on different sides. For normal components of electric displacement vector, we in analogy get: Dnorm 1 = Dnorm 2. Dealing with magnetic field, tangential components of H and normal components of B have to meet similar conditions. If one medium is perfectly conductive for electric currents or magnetic ones, boundary conditions can be divided to Dirichlet condition and to Neumann one. Dirichlet condition expresses the fact that the component of electric (magnetic) field intensity, which is tangential to the perfect electric (magnetic) conductor, has to be zero
Neumann condition expresses the fact that derivative of the electric (magnetic) field intensity vector in the normal direction to the perfect magnetic (electric) conductor has to be zero
PEC denotes Perfect Electric Conductor, PMC denotes Perfect Magnetic Conductor and n is a normal to the conductive surface. Cartesian coordinate systemIt consists of three rectilinear mutually perpendicular basis vectors x0, y0, z0 (see figure). In this system, an arbitrary point is described by the vector
Differential operators are described by the following relations:
CausticsAssume that a wave radiated by a point source propagates through the medium with the unitary dielectric constant first, and then continues through the layer which dielectric constant decreases down to a certain minimum, and then rises to 1 again. In a certain part of the layer, beams return by curls back to the source. Tops of the curls can be connected by an imaginary spline, which is not crossed by any beam, and in a close vicinity of which (below) two neighboring beams intersect. This spline (or a surface in space) is called caustics. Cavity resonatorCavity resonators belong among microwave circuits. As a cavity resonator, dielectrics of an arbitrary shape can be used, which is bounded by a conductive surface. Resonant frequency is given by dimensions and a shape of dielectrics, parameters of dielectrics, and by a mode of oscillations. Quality factor of cavity resonators varies from 103 to 105. Characteristic impedanceCharacteristic impedance Z0 is an important parameter of the transmission line. If the transmission line is ended by the complex impedance Z0, all the energy is transmitted by the line and there is no reflection. If the ending impedance is different, a part of the energy is reflected back to the source. A standing wave is formed then over the transmission line. The characteristic impedance is equal to the ratio of the voltage over the current of the transit wave. In an ideal transmission line Z0 is real and there are no losses in the tranmission line. In a normal transmission line there is a small imaginary part. The value of the characteristic impedance depends on the radius, the shape and the dielectrical constant of the transmission line. Charge cellCharge cell is shifted for one half of the discretization element with respect to the current cell. The center of the charge cell appears at the edge of the current cell. This center is identical with the point, where the value of charge is computed. Coherent radiationRadiation exhibits time-coherence, if identical phase shift Δφ can be measured whenever and everywhere for a given time interval Δt. Radiation exhibits space-coherence, if identical phase shift Δφ can be measured whenever and everywhere for a given spatial distance Δl. Collocation methodMethod of weighted residua is called the collocation method when Dirac pulses play the role of weighting functions. Continuity equationContinuity equation describes the mutual relation between the time variation of a charge in a closed volume and currents, which flow out of this volume
Outflow of current (divergence of current density) is equal to the decrease (therefore minus) of charge density per second. Coulomb lawAssume two charges Q1 and Q2 in vacuum in the mutual distance d. Charges are of the opposite polarity and do not move. The charges mutually attracts by a force, which magnitude is
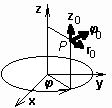
The above-given relation expresses Coulomb law. The symbol π denotes Ludolf number and ε0 is permittivity of vacuum (ε0 = 8.85 * 10-12 F * m-1). Critical frequencyCritical frequency of a mode in a waveguide specifies a frequency, when the mode starts to propagate in the waveguide. If frequency is lower than the critical one, then the mode does not propagate. Cross polarizationCross polarization equals to the ratio of an electric-field intensity component in a given plane (E or H) and of a component, which is perpendicular to the previous one. Crystal latticeIdeal crystal lattice is a model arrangement of atoms in the volume of material. This arrangement has a periodic character and can be described by the elementary cell, representing by a parallelepiped with the edge of length a in which individual particles are located. Edge length a is called the lattice constant and it is an important parameter to describe the crystal structure. Current cellCurrent cell is identical with the discretization element in the analysis of planar antennas by moment method. Over the surface of the current cell, a constant value of current is usually assumed. Current distributionCurrent, which flows into the dipole, reflects from the ends of the arms and returns back to the generator. The forward current and the backward one interfere. In the position, where the forward current and the backward one are of the same phase, the maximum amplitude of the current appears. In the position, where the forward current and the backward one are of the opposite phase, the minimum amplitude of the current appears. Spatial course of the current amplitude is called the current distribution. Current inductionIf electromagnetic wave impacts a conductor, free charge carriers are set into a motion (induced currents appear). Induced currents become a source of the secondary wave, which interferes with the primary one (impacting the conductor). The component of the total electric field intensity vector, which is tangential to the conductive surface, is very small (is zero if the conductor is perfectly conductive). Cylindrical coordinate systemIt consists of a single curvilinear basis vector φ0 and two rectilinear basis vectors r0, z0. Basis vectors are mutually perpendicular (see figure). In this coordinate system, an arbitrary point is described by the vector
Differential operators are of the following form:
Cylindrical waveCylindrical wave is characteristic by the cylindrical shape of the equiphase surface. Infinitely long conductor flown by an alternate current can be the source of the cylindrical wave, e.g. De-embeddingThe above-given term denotes such a way of computing reflection (transmission) coefficient from voltage and current of a localized source so that they correspond to the measurement when long cables are used. Diffraction factorDiffraction factor is proportionality constant between the amplitude of diffraction waves and the amplitude of the incident wave. Dirac pulseDirac pulse is an infinitely narrow pulse (is non-zero in a single point), and infinitely high pulse (the functional value tends to infinity in this single point). The filtering property of Dirac pulse is of highest importance. Since Dirac pulse D (x-x0) is non-zero in x0 only, integration produces the functional value of f in x0. Directivity factorDirectivity factor D(φ, ϑ) quantifies antenna radiation in different directions. Considering isotropic radiator, directivity factor is unitary for all the angles φ a ϑ. Dealing with real antennas, directivity factor is higher than one for those directions, where radiations is concentrated by the antenna, and lower than one for those directions, where the radiation is suppressed. Directivity pattern of the antennaDirectivity pattern is a graphic representation of directional properties of the antenna. Directional properties are usually expressed in the form of the absolute value of the radio of electric intensity of the radiated wave in a given direction and its maximum value (computation is performed for the far field of the antenna). Directivity pattern is usually drawn for a certain plane (e.g., plane perpendicular to the dipole, plane containing the dipole). Duality principleInvestigating Maxwell equations
we can simply understand, that exchanges
transform the left-hand side of equations to right-hand side and vice versa. Performing similar exchanges, the solution of right-hand set of equations can be obtained from the solution of left-hand side set under the same boundary conditions. E.g., two similar tasks are assumed, which differ by feeding (electric current in the first case, magnetic current in the second one) only. Solution of the first task is based on the left-hand couple of equations (1), (2), solution of the right-hand task on the right-hand couple. Solution of the first task is known, solution of the second task is rather problematic. According to the duality principle, solution of the second task is obtained by exchanging (3) in the result of the first task. Conditions for the application of the duality principle are met at complementary objects. Two complementary objects are two planar objects. At the first one, a part of the plane is conductive (metal), the rest is not conductive (air). At the second object, the situation is reverse. E.g., a slot is complementary to a conductive strip, both the slot and the strip have to be of identical dimensions. In the strip, electric current can be excited, and the strip radiates as a dipole. In the slot, magnetic current is excited. Relation for slot radiation is the same as relation for dipole radiation if exchanges (3) are done. Dyadic Green functionDyadic Green function is a function of the proportionality between the current density vector J and vector potential A . Dyadic Green function can be imagined as a matrix of the size 3 x 3, where each element is a function. E.g., the function in the first column and in the second row gives the contribution of the current component Jx to the potential component Ay, etc. Edge finite elementsEdge finite elements are used to the approximation of a vector quantity in an analyzed structure. In the simplest case, the vector quantity is approximated over a finite element by a linear combination of vector functions, which are unitary vectors along a single edge of the element (different one for every function), and which are zero on the rest of edges. If partial vector functions are multiplied by the magnitude of the projection of the approximated quantity to the respective edge of the element and is the products are summed
we get approximation of vector quantity E over nth finite element E~(n). In the above-given relation, Em(n) is the edge value (projection magnitude) of the vector E to mth edge of nth element (a triangular one because the summation is performed over three vertexes) and Nm(n) is a vector function, which is unitary on mth edge of nth element and which is of the same orientation as the edge. Effective permittivityAnalysis of structures, which consist of several dielectric layers (a substrate and air, e.g.), is rather complicated (boundary conditions have to be met on all the boundaries). Approximate solutions therefore replace inhomogeneous dielectrics by such homogeneous one, so that electromagnetic properties of the original structure are kept unchanged. Value of permittivity of such substitutive homogeneous dielectrics is denoted as effective permittivity. EiconaleEiconale is such a scalar function of coordinates which gradient (the direction of the steepest descent of the function) is identical with the direction of wave propagation in every point. Electrically thin substrateThe above-given term denotes a dielectric substrate, which height is much smaller compared to wavelength in that substrate. Elementary electric dipoleAssume an ideal dielectric (no free charges). Positive and negative charges form together neutral atoms (charges can move inside the atom only). If static external electric field takes the effect, then atoms keeps the neutrality in their whole, but the gravity center of positive and negative charges shifts. Atoms are polarized (atoms become electric dipoles).
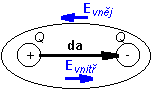
Electric dipole is described by the moment of electric dipole p [C.m] where da is a positional vector from the negative pole of the atom to the positive one, and Q is charge on poles. If external electric field varies in time, even the magnitude of a charge at the ends of the dipole changes a corresponding way. The changes of the magnitude of charge can be imagined being caused by a current flowing through the dipole (see continuity equation). Elementary loop, magnetic dipoleIn every atom, electrons move around the kernel. This movement of electrons along orbits can be imagined as a current loop, flowing by current I. Since electrons in motion create magnetic field, effects of the elementary current loop can be described by the moment of magnetic dipole
where dS is the vector of the surface bounded by the current loop. In ferromagnetic, external magnetic field causes such skewing of current loops so that moments of magnetic dipole approach the direction of the external magnetic induction. That way, the external field is amplified inside the ferromagnetic. Elementary loop can be considered as the simplest loop antenna (elementary magnetic dipole). Equiphase surfaceEquiphase surface is a surface of a constant phase of a wave. On the equiphase surface, amplitude can be constant (uniform wave) or can vary (non-uniform wave). Evanescent waveEvanescent wave is not a real wave in a fact. Phase does not change in the propagation direction because phase constant is zero. Amplitude exponentially decreases because attenuation constant is non-zero. Evanescent wave can appear (under certain circumstances) on the boundary of two media when wave propagates in parallel with the boundary in one medium. Then, the wave does not enter the second medium, but electromagnetic field diffuses there (evanescent wave). Far-field regionFar-field region is given by the distance from the antenna to infinity (d is the largest transversal dimension of the antenna, λ denotes wavelength). For far-field region, trajectories of waves radiated from various parts of the antenna can be assumed to be in parallel. Field intensity created by Huygens sourceHuygens source (infinitely small facet dS) illuminated by the wave of the intensity E(S) from one side, which is a part of larger planar surface (also illuminated), creates a spherical wave on to non-illuminated side, which is of the following intensity in the distance r
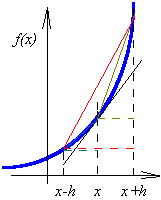
Angle ϑ is the angle between the normal to dS and the radius vector of the observation point. Finite differencesFinite differences are used to replace the value of a derivative in such situation, when the derivative cannot be evaluated. The derivative of the function f in the point x determines the tangent direction of a function in a given point (black line in Figure). This direction can be approximated exploiting the red rectangle as
If the point x is in the middle of the interval then we speak about the central differentiation. Red line and black one seem to be very similar. Except of the central differentiation, the forward differentiation (dark-yellow rectangle) and the backward differentiation (cyan triangle) exist. Nevertheless, the difference between the dark-yellow line and black one (or a cyan line and black one) is more significant than in the case of the central differentiation. Finite elementThe term finite element denotes a spatial discretization element where the examined quantity is of a finite energy. A finite element can be even of an infinite extent if an examined quantity satisfactorily quickly decreases to zero over its area. E.g., energy of electromagnetic field is finite over an infinitely large element covering the area from a very long distance from the source to infinity. In one-dimensional space, the finite element is of the form of an abscissa (the examined quantity is approximated over finite element by an abscissa, which is given by the values of the quantity in marginal points (nodes). In two-dimensional space, the finite element is of the form of a triangle (the quantity is approximated by a plane given by three points - nodal values in vertexes). In three-dimensional space, the finite element is of the form of a tetrahedron. Finite-element methodFinite-element method is a general numerical method of solving partial differential equations. The method consists of the following steps:
FocusThe term focus denotes a point where beams intersect. Folded dipoleFolded dipole consists of a symmetric dipole and a near conductor, which is positioned in parallel to the dipole and which is of the same length as the dipole. Ends of the dipole are connected to the ends of the parallel conductor. The center of the parallel conductor (in front of the feeding gap) is of zero potential. The folded dipole is of wider frequency band and of higher input impedance compared to the symmetric dipole. Fourier seriesSpectrum of a signal s(t), which is periodic with the period T1, is discrete, and its k-th component is given by the relation
In the above-given relation (Fourier transform of a signal s), ω1 = 2π/T1 denotes angular frequency and asterisk denotes complex conjunction. If spectral components ck are known, then time course of the signal can be reconstructed
The above-given relation is called Fourier series. Frequency selective surfaceFrequency selective surface can be imagined as a dielectric layer of very large extent, which contains planar conductive elements on its true side and which backside is free (without any metallic part). Planar conductive elements can be arbitrarily shaped, but within one selective surface, all the elements are usually identical. Conductive elements can be conductive (electrically conductive elements) or can be implemented as slots in continuous metallic true side (magnetically conductive elements). If the true side of the selective surface is illuminated by harmonic waves of various frequencies, some waves are transmitted with a minimum attenuation, some waves are totally reflected back to the half-space of the source, and some waves are partially transmitted and partially reflected. Hence, the surface performs a frequency selection of incident waves. Fresnel diffractionThe term Fresnel diffraction describes the wave diffraction, which appears when wave transmits a cut in a thin planar obstacle. The obstacle neither transmits nor reflects the wave. Fresnel integrals, klothoidyFresnel integrals are given by the relation
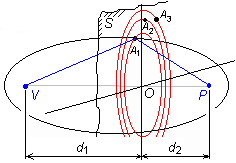
Their values can be computed by numerical integration in matlab, can be found in tables, can be read from klothoidy. Klothoidy is a graphical representation of Fresnel integrals. On the horizontal axis, there is a real part of the integration result C(x ), on the vertical axis, there is an imaginary part of the result S(x). In the above-described coordinate system, Fresnel integrals are of the form of a spiral curve, which is scaled by the parameter x. If the value of Fresnel integrals is computed for a given value of argument x0, the value of argument is found on the scale of the spiral curve, and then, the value of integrals C(x0) and S(x0) is directly read on the horizontal axis and the vertical one. Fresnel zonesIn free space, assume a transmitter V and a receiver P as depicted in the figure. In an arbitrary planar cut, which is perpendicular to the line VP, such points A1 are searched so that the pointed line VA1 P can be half wavelength longer than the direct distance VP. There is infinite number of such points and form together a circle of the center in O . Surface bounded by this circle is so called first Fresnel zone, and OA1= r01 is its radius. The same way, the other points A2, ... An can be found, which meet
The annulus surface between A2 and A1 is the second Fresnel zone, etc. Radius of nth zone can be computed using the approximate relation
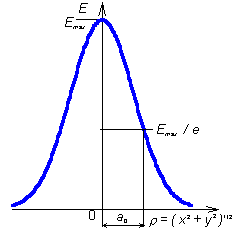
Repeating the above-described consideration for points A1 in different positions (cuts) along the line VP, different values of the radius of the first Fresnel zone are obtained. All the points A1 are part of a rotational ellipsoid, which is called the first Fresnel ellipsoid. Full-wave methodsFull-wave methods are based on the electromagnetic field description by complete Maxwell equations. Validity of full-wave methods is not frequency-limited. On the other hand, full-wave methods require adoption of numerical approaches (analytical solution of Maxwell equations is not known for planar structures), and hence, high computational power is needed. Galerkin methodIf weighting functions are identical with basis ones in the method of weighting residua, we speak about Galerkin method. Gaussian beam, Gaussian functionAssume a laser beam of the basic mode TEM00 , which leaves the source as parallel (equiphase surface is planar and perpendicular to the direction of propagation, to the optical axis). Although the beam is not intentionally modulated, transversal field distribution is not constant. Considering the above-mentioned mode, the maximum intensity is in the axis of the beam, and the intensity decreases towards margin of the beam following Gaussian function:
Here, r is radial distance from the axis of the beam, and the function is depicted in the figure. Beam, which is characteristic by the above-described transversal Gaussian distribution of field intensity, is called Gaussian beam.
General theory of diffractionGeneral theory of diffraction deals with the wave diffraction on obstacles of an arbitrary shape. Since the general approach is rather complicated, results for relatively simple geometries are usually used only, and real obstacles are tried to be approximated by these objects (e.g., a conductor of finite length can be assumed as an extremely long ellipsoid). Geometric theory of diffractionGeometric theory of diffraction (GTD) is an extension of geometrical optics to the medium containing discontinuous inhomogeneities. We solve the interaction of beams and obstacles, and laws of geometrical optics are completed that way, so that obvious incorrectness (discontinuities on the boundary of reflection region and shade one) are eliminated on one hand, and the advantages of the geometrical optics (the idea of beams) are preserved on the other hand. Geometrical opticsGeometrical optics is a method for the solution of wave phenomena in complex media. The method adopted the conception of wave propagation along beams from the classical geometrical optics. On the contrary, geometrical optics enables us to compute amplitude and phase variations of field intensity and wave polarization when wave propagates in the media of continuously changing parameters. Global basis functionsGlobal basis functions are of non-zero value over the whole analyzed area. As global basis functions, harmonic functions or Bessel ones are usually used. Green functionGreen function is a function of the proportionality between the current density vector J and vector potential A. Hankel functionsBessel differential equation is met even by the linear combination of Hankel functions of the first kind Hn(1)(x) and of the second kind Hn(1)(x)
Hankel functions meet
Hertz vectorAssume ideal dielectrics, which is polarized by the external electric field. The vector of enforced electric polarization Pvn describes polarization. Then, electric displacement vector can be expressed as
Substituting electric displacement vector D (1) to the first Maxwell equation, and assuming zero enforced current Jvn = 0 (induced current is zero too, because the ideal dielectrics is of zero conductivity)
Then, the third Maxwell equation can be rewritten to
On the basis of (2) and (3), wave equation for vector potential can be obtained
For the scalar potential, we get
We express potentials A and φ using an auxiliary vector Πe
Substituting (6) to wave equation (4) and (7) to (5), we get
If vector πe is determined to meet the equation
even (8) and (9) are met at the same time. That way, solution of Maxwell equations is transformed to the solution of a single inhomogeneous equation when Jvn = 0. Hertz discovered this possibility, and the vector Πe is therefore called electric Hertz vector. In dual way, magnetic Hertz vector can be introduced. Huygens principleHuygens principle says that every point of a closed surface S (more accurately, every elementary facet dS), which is illuminated by a wave arriving from outside, behaves as a source of an elementary spherical wave for the region inside the surface. Huygens source, elementary sourceThe term Huygens source denotes infinitely small facet dS, which is illuminated by an incident wave from one side. Applying Huygens principle, this facet becomes a source of an electromagnetic wave. Real surface sources of waves (horn antennas, slot antennas, illuminated parabolic reflector) can be considered then as a set of Huygens sources. Hybrid finite elementsIf a shielded microstrip transmission line is analyzed using hybrid finite elements, all the components of electric field intensity or all the components of magnetic field intensity are included into the computation. The matter of hybrid finite elements consists in modeling a longitudinal intensity component by nodal approximation, and in modeling transversal intensity components by edge-vector approximation. Impedance bandwidthImpedance bandwidth can be defined as a frequency interval, where 90% of supplied energy enters the antenna (10% energy is reflected back to the generator). The described situation corresponds approximately to the standing wave ratio equal 2. Impedance transformerOn high frequencies, impedance transformer plays the same role as the classical transformer on lower frequencies: voltage, current and impedance are transformed. Transformers differ in their construction. As the simplest impedance transformer, one-quarter-wavelength-long transmission line can be used. The following relation describes such transmission line:
Here, Z0tr 2 is squared value of characteristic impedance of transmission line. If the impedance Z0out ends the transmission line, then the impedance Z0in appears at its input. Inhomogeneous wave equationThe term homogeneous wave equation denotes the equation of the form
This equation is valid for Cartesian coordinate system. If vector E meets the equation then this vector describes wave propagation. If right-hand side of the equation is zero, we are far away from the sources and wave is a source of a wave. The right-hand side of the inhomogeneous wave equation is non-zero in contrast to (1)
In the right-hand side of (2), time derivative (jw) of the source current Je is present. This equation has to be applied if regions near sources (antennas) are investigated. Input impedance of the antenna, radiation impedanceInput impedance of the antenna can be measured at the input port of the antenna. Input impedance consists of the radiation resistance RΣ (when multiplied by the squared input current Ivst2, real radiated power is obtained), of the loss-making resistance Rztr (Rztr Ivst2 equals to the power, which is converted to the heat in the antenna and its surrounding) and of the radiation reactance XΣ (describes the mutual energy exchange between the antenna and the electromagnetic field in its surrounding). Radiation resistance and radiation reactance form the radiation impedance together. Ionospheric layerThe ultra-violet radiation of Sun ionizes atmospheric gases - the fission of molecules or atoms produce a positive ion and a negative electron. An ionized layer of atmosphere is called the ionosphere. The ionosphere begins in the height of 40 km from the earth surface. Concentration of electrons in the ionosphere varies with height, and significant local maxims can be observed. Intervals around local maxims are called ionospheric layers. If electromagnetic wave impacts the ionospheric layer, then the wave trajectory is curved, and under proper conditions, the wave can return back to the earth. Isotropic medium, anisotropic mediumIsotropic medium is of the same electric and magnetic properties in all the directions (of the same permittivity and permeability). Therefore, magnitude of the x-component of electric displacement density Dx depends on the magnitude of the x-component of the electric field intensity Ex only:
From the mathematical point of view, permittivity and permeability are scalar quantities. Anisotropic medium is of different properties in different directions. Therefore, the x-component of the electric displacement density Dx depends (in general) on all the three components of electric field intensity:
From the mathematical point of view, permittivity and permeability are tensors, i.e. matrices of the size 3 x 3. Plasma, where steady magnetic field exists, or steady-magnetized ferrite, are examples of anisotropic media. Lagrange interpolation polynomialsLagrange polynomial of degree n can be in general expressed using the simplex coordinate x as
Here, n is degree of the approximation polynomial. Equation describes the whole family of polynomials; members of the family differ an index m, which can vary from zero to n. Nulls of polynomials Rm(n) are equidistantly distributed on coordinates x=0, 1/n to (m-1)/n, polynomial is of unitary value in x = m/n. Therefore, Rm(n) contains m equidistantly distributed nulls on the left from x = m/n and no null on the right. Linear antennaLinear antenna can be composed of a finite number of elementary dipoles. On the contrary, planar antennas can be composed of a finite number of Huygens sources. Linear combinationThe term linear combination of vectors (functions) denotes such vector (such function), which is obtained by adding primary vectors (primary functions) that are multiplied by arbitrary scalar non-zero coefficients. Linear mediumPermittivity and permeability of a linear medium are constants, which are independent on intensities E and H. If electric field intensity is increased then electric displacement density proportionally rises. If magnetic field intensity is increased then magnetic flux density proportionally rises. Local basis functionsLocal basis functions are of non-zero value over a single (or a few) discretization element, and over the rest of elements, they are zero. Piecewise constant or piecewise linear function are typical representatives of local basis functions. Longitudinally homogeneous waveguideThe term longitudinally homogeneous waveguide expresses the fact that waveguide parameters are constant in the longitudinal direction. If the waveguide is lossless, only phase of the wave changes in the longitudinal direction (amplitude stays constant). Lorenz forceThe force acting on a charged particle depends only on its position, speed and amount of charge. The force acting on the elementary charge can be written as
where E and B is the electric field and magnetic induction at the position of the hub. Matrix optics, matrix of beam, ABCD lawMatrix of beam is a matrix of size 2 x 2, which describes changes of Gaussian beam parameters when passing through an optical element. If matrix is multiplied (from the right-hand side) by a column vector, which contains beam parameters at the input of an optical element, we obtain a column vector of beam parameters at its output. The relation is called ABCD law. Due to the matrix nature of above-described operations, we speak about matrix optics. Method of induced electromotoric forces, mutual impedance, self-impedanceThe method helps us to compute voltages, currents and impedances in antenna systems. The method understands the voltage, which is observed at the input port of every single antenna element, being induced by the radiation of all the antenna elements (including the own element). The voltage can be composed from contributions of single elements. Each contribution is proportional to the current of the respective element. E.g., voltage U1 at the input of the first antenna element equals to the summation where I1, I2, I3 are currents at the input ports of single elements, Z11, Z12, Z13 are impedances. Z11 is self-impedance, Z1n are mutual impedances between the first element and the other elements in the antenna system. These impedances depend on the mutual position and mutual distance of antenna elements. Microstrip antenna, microstrip dipole, patch antennaThe term microstrip antenna denotes all the antennas, which are fabricated by the microstrip technology. In this textbook, a microstrip dipole (narrow microstrip conductor on the true side of the substrate, which is interrupted by a feeding gap) and a patch antenna (rectangular antenna element of the true side of the substrate, which can be fed by a microstrip, by a coaxial probe, or by an aperture in the ground plane) belong to this class of antennas. Microstrip transmission line, ground planeMicrostrip transmission line consists of a very thin and relatively narrow strip line, which is placed to a true side of a dielectric substrate. The backside of the substrate is covered by continuous metallic layer and serves as a ground plate of zero potential. The whole transmission line is usually put into a rectangular waveguide, which plays to role of shielding. All the metallic parts of the structure (microstrip, ground plate, metallic waveguide) have to be fabricated from a well-conducting electric conductor in order to reach as low attenuation as possible. Considering the same reason, dielectric substrate has to be of as low losses as possible. Microwave frequency bandMicrowave frequency band denotes the interval of frequencies from 300 MHz to 300 GHz. Those frequencies correspond to the wavelengths from 1 m to 1 mm in a free space (in vacuum). Mirror principleThe mirror principle enables simple modeling of the effect of well-conductive planes, which are near a radiating antenna. The radiation induces currents on the surface of the plane, which contribute to the antenna radiation as well. According to the mirror principle, contribution of induced currents equals to the contribution of a mirror images of real antenna elements. A vertical element mirrors with a current of the identical amplitude and phase. A horizontal element mirrors with a current of the identical amplitude and opposite phase. Modal analysis of patch antennasFor modal analysis the planar antenna is modeled as a resonant cavity with perfect electric walls at the top and bottom. The main restriction is that the thickness of the dielectric substrate must be much smaller than the wavelength. Then the variance of the electric field in the plane perpendicular to the patch (axis z) is negligible. Because of the applied boundary conditions the electric field is non-zero only along the axis z, whereas the magnetic field has non-zero components only in the x-y plane. Along the boundaries of the metallic patch the Neumann condition for electric field is valid. It expresses the fact that the derivative of the electric field intensity vector normal to the perfect magnetic conductor has to be zero (∂E/∂n = 0). It implies the boundaries of the patch can be considered as perfect magnetic conductor. Modes, mode numbers, dominant mode, band of unimodalityWaves propagating in a waveguide are characterized by a given transversal field distribution. The wave of a given transversal field distribution is denoted as a given mode of a wave. Every mode can be characterized by a given critical frequency, a given phase velocity, a given wavelength and a given group velocity. The mode of the lowest critical frequency is called the dominant mode. The frequency band, in which a single mode of a wave propagates in the waveguide, is called the band of unimodality. Every mode is characterized by integer constants. Those constants are called mode numbers. Considering rectangular waveguide, mode numbers specify the number of half-waves of standing waves in the directions of transversal coordinates. E.g. TM11 (transversal magnetic wave) is of a single half-wave of the longitudinal component of electric field intensity in x and a single half-wave in y (if z is identical with waveguide axis). Considering TE10 (transversal electric wave, the dominant mode of a rectangular waveguide), a single half-wave of the longitudinal component of magnetic field intensity appears in x, and in y , this component is constant. Moment method in spectral domain, spatial domainTemporal-spatial distribution of electromagnetic field is described by the term exp[j(ω t-kr)], where ω is angular frequency (a change of a phase over one second), t denotes time, k is wave-number (variation of phase over 1 meter in a given direction, i.e. spatial frequency), and r denotes length (in a given direction). Space-domain analysis is based on computations for a single value of the spatial frequency k (the distance r is a variable). In spectral-domain analysis, the distance r is considered as a constant, and computations are performed for all the possible spatial frequencies k. Moment method, moment solutionMoment method is a numeric method of solving integral equations (a sought function, e.g. current distribution on the antenna, is included in the integrated function). The method consists in the discretization of the analyzed structure, in formal approximation of the sought function (known basis functions and unknown approximation coefficients), in substituting the formal approximation to the solved equation (unknown approximation coefficients are removed from the integrated function and known basis functions are integrated), in minimizing the approximation error (the solved equation containing the formal approximation is sequentially multiplied by Dirac pulses in the center of discretization elements and the product is integrated over the whole analyzed structure - we obtain N equations for N unknown approximation coefficients) and in solving the final matrix equation (unknown approximation coefficients, and therefore, the approximation of the solution is obtained). Moment tableThe term moment table denotes a matrix, which contains mutual contributions among single charge cells and current ones. Nodal finite elementsNodal finite elements serve to piecewise continuous approximation of a scalar quantity in an analyzed structure. In the simplest case, the scalar quantity is approximated by linear function over a finite element. The linear approximation is composed of partial linear functions, which are unitary in a given vertex of the element (different one for every function) and which are zero in the rest of vertexes. If partial linear functions are multiplied by the value of the approximated quantity in such vertex of the element (in such node), where the function is of unitary value, and the products are summed we get a linear approximation of E over nth finite element E~(n). In the above-given relation, Em(n) is a nodal value of the quantity E in mth node (vertex) of nth finite element (a triangular one because the summation is performed over three vertexes) and Nm(n) is a linear function, which is unitary in mth node of nth element. Considering the above-described nodal approximation, the nodal values of the quantity Em are spatial samples of the approximated quantity E. Nodal valueThe term nodal value denotes the value of a sought function in a given, exactly defined point (node). If piecewise constant approximation is used, then nodes are usually positioned to the center of discretization elements. Parallel polarization of waveIn the case of the parallel polarization, the vector E of the wave is parallel with the plane of incidence. Paraxial wavesParaxial waves are waves, which directions of propagation are nearly the same (they mutually decline for a very small angle). We speak about paraxial waves if their sum is of a special meaning. E.g., a single non-uniform wave propagating in z-direction can be expressed as a sum of paraxial uniform waves, which propagate in directions those slightly decline z. Perpendicular polarization of waveIn the case of perpendicular polarization, the vector E of the wave is perpendicular to the plane of incidence. Perpendicular polarization, parallel polarizationPolarization describes orientation of the vector of electric field intensity of a wave. If wave propagates near the boundary of two media, we distinguish the perpendicular polarization and the parallel polarization. First, the plane of incidence is defined as a plane, which is perpendicular to the plane of boundary and which is parallel to the direction of propagation. The vector E of the perpendicularly polarized wave is perpendicular to the plane of incidence. The vector E of the wave polarized in parallel is parallel to the plane of incidence. If the plane of boundary is identical with the earth surface, then perpendicular polarization is called horizontal polarization, and the parallel polarization is called the vertical polarization. Phase velocity, group velocityPhase velocity determines the change of phase of wave per second. Phase velocity is not associated with the velocity of energy transmission, and therefore, it can be higher than velocity of light in vacuum c = 3 * 10+8 m/s. Phase velocity tends to infinity in all directions lying on the equiphase surface (i.e. on the surface associating points of the same phase): the phase changes for 2π radians within infinitely short time period here. On the other hand, group velocity determines the speed of energy transmission. Since in the directions, which lie on the wave-surface, energy is not transmitted (wave-surface is perpendicular to the propagation direction), group velocity is zero here. In common media, phase velocity and group one are mutually related according to
Here vf denotes phase velocity, vg is group velocity, and v is free-space velocity of light. PhononThis is a quasi-paticle, which was introduced to represent the quantum vibrational energy of the crystal lattice. Using these particles we can describe the propagation of sound (mechanical) waves in crystals. Planar microwave transmission lineThe term planar microwave transmission line denotes a structure consisting of a metallic planar ground plate and of one or more plan-parallel planar conductors (metallic strips as electric conductors or slots in metallic plate as magnetic conductors). Various dielectric layers differing in their electric or magnetic parameters can complete the structure. Planar transmission line can be open (just described) or shielded (placed into a metallic waveguide. Plane E, plane HMagnetic lines of waves radiated by the antenna determine the plane H. Considering the dipole, plane H is perpendicular to the axis of the dipole. Electric lines of waves radiated by the antenna determine the plane E. Considering the dipole, all planes containing the dipole are plane E. Plane of boundaryPlane of boundary is a plane, which separates two media of different electric properties and magnetic ones. Plane of incidencePlane of incidence is perpendicular to the plane of boundary and is parallel with the propagation direction of the incident wave Plane wavePlane wave is characteristic by the planar equiphase surface (connecting points of the same phase, a plane is obtained). As a plane wave, we can consider a wave in a very long distance form the source when observed in a very small part of the space (in the frame of a large region, the wave is already of the spherical nature). Point sourceThe term point source denotes such source of electromagnetic waves, which the only ability is the radiation ability. The source is of zero weight and zero size. Polarization of dielectricsDielectrics do not contain free charge carriers. Dielectrics consist of atoms, where the positive charge of the kernel equals to the negative charge of the electrons. If the dielectrics are inserted into the external electric field, the kernel of positive charge is deflected in the contra-direction of the external electric-field intensity, and electrons of the negative charge are deflected in the direction of the external electric field. In dielectrics, an inner electrical field appears, which intensity is of the opposite orientation than the intensity of the external one. Therefore, the external electric field is weakened in the dielectrics. Poynting vectorFrom the mathematical point of view, Poynting vector can be computed as vector product of electric field intensity vector and complex conjugated magnetic one. Direction of Poynting vector is identical with the direction of energy propagation. In most situations, magnitude of Poynting vector equals to the surface power density of a wave. Propagation constant, attenuation constant, phase constantPropagation constant γ describes variation of amplitude and variation of phase of a wave in the longitudinal direction in a waveguide. Propagation constant is given by the relation
Here, β is attenuation constant and α is phase constant). Attenuation constant describes the amplitude decrease on the trajectory 1 meter long; the amplitude decreases to exp(-β) - multiple of its initial value. Phase constant describes the phase variation on the trajectory 1 meter long in the direction of wave. Quality factor of a resonatorQuality factor of an arbitrary resonant circuit of angular frequency ω0 is given by where W is energy of electromagnetic field in a circuit, and PZ is lost power in a circuit. Quasi-static analysis, full-wave analysisQuasi-static analysis of a microstrip transmission line consists in modeling a dominant mode (mode quasi-TEM) propagating along the line, by a transversal electromagnetic wave. Field distribution of such wave can be determined by a static analysis of the structure (microstrip is assumed to be of the potential 1 Volt, the shielding waveguide is grounded). Quasi-static analysis gives good results typically below 5 GHz. If a microstrip transmission line is going to be analyzed on higher microwave frequencies, then full-wave methods have to be applied, which are based on a direct solution of Maxwell equations. Quasi-static methodsQuasi-static methods of the analysis of planar microwave transmission lines are based on the assumption that the dominant wave propagating along the microstrip transmission line can be satisfactorily approximated by the transversal electromagnetic wave, TEM. Then, transversal components of the dynamic electromagnetic field are close to the components of the static field. Therefore, the approximate field distribution in the transmission line can be obtained by solving Laplace equation for scalar potential. RadomeThe term radome denotes an antenna cover, which should protect an antenna to the influence of the surrounding (rain, insects, birds, etc.). The antenna cover should even form a proper interface, which enables to reach desired properties of the antenna (minimal transmission losses, minimal influence to antenna parameters, etc.). Rayleigh distanceFrom a certain distance (Rayleigh distance), wave does not propagate in directions, which correspond to the parallel beams, but it propagates in directions, which correspond to divergent beams. Reflection coefficient, transmission coefficientReflection coefficient is defined as a ratio of the magnitude of a certain component of electric field intensity of a wave, which is reflected from an obstacle, and the same component of electric field intensity of incident wave. As an obstacle, we assume an object, which is large enough in the direction transversal to the direction of wave propagation (there is no diffraction there). The obstacle is of different electrical parameters than the surrounding. Transmission coefficient is defined as a ratio of the magnitude of a certain component of electric field intensity of a wave, which transmitted through an obstacle, and the same component of electric field intensity of incident wave. Reflector antennasReflector antennas consist of a primary radiator (a dipole, e.g.) and a reflector (parabolic one, e.g.). If plane wave is incident to such a reflector, the reflector concentrates all the energy in the focus. If a primary antenna is positioned to the focus, a strong power appears at its output. Refractive indexRefractive index is given by the ratio of wave number in a given medium and wave number in the vacuum. In lossless medium, we get
Other words - refractive index says, how longer is wavelength in the vacuum comparing to the wavelength in a given medium. Resonant resistanceThe term denotes input resistance of a patch antenna in resonance (the patch length equals to the half of wavelength). Magnitude of resonant resistance can be influenced by the patch width and by the position of the antenna input (in patch is fed by a microstrip, then feeder is immersed into the patch). Scalar Green functionScalar Green function is a function of the proportionality between the charge density ρ and scalar potential V. Scalar potentialScalar potential simplifies the investigation of the influence of static charges (time derivative equals to zero). Field is then described by the first and the third Maxwell equation in the form
Since curl of gradient identically equals to zero, (1) is met if
(j is scalar potential). Hence, the single scalar equation (Laplace one) has to be solved
Eqn. (3) is valid in every region, where potential is finite and continuous. Thanks to (3), the field is described by a single partial differential equation for a scalar function j. Physical notion j can be built on the basis of (2)
Since the product E .d r equals to the work, which is performed by the field when moving unitary charge along the elementary path dr, elementary potential dj equals to the decrease (therefore minus) of the potential energy of this unitary charge in electrostatic field. Shape functionThe term shape function denotes a partial approximation function over a single finite element, which is unitary in a single node and which is zero in the rest of nodes. Among the most frequently used shape functions, a liner function belongs: a plane, which is unitary in a single node and which slopes down to zero in the rest of nodes. All the shape functions, which are unitary in a common node, form a basis function together. In a two-dimensional case, linear basis function is a pyramid, which is unitary in a common node, and which slopes down to zero on edges of all the finite elements, which share the common node. Sign conventionTemporal-spatial distribution of a harmonic wave is usually described by the term exp(+jwt - jkr), where angular frequency ω describes the phase change within one second and wave-number k the phase change within one meter. Moving in time, the phase increases. Moving in space in the direction of propagation, the phase decreases. If signs in the exponential term are swapped to exp(-jwt+ jkr), then the matter of studied phenomena does not change (all the laws stay valid). Nevertheless, we have to say which sign convention is used and we have to keep the same convention during the whole computation. If some mathematical relation is going to be transformed from one convention to the second one, only signs at all the imaginary units have to be changed (+j « -j). Simplex coordinatesConsidering triangular finite element, simplex coordinate axes are of the same orientation as the triangle heights. Simplex coordinates are unitary in the vertex and zero on the opposite edge. Simplex coordinates depend neither on the shape nor on the size of the triangle. Therefore, computations can be performed for only one finite element, and results can be recomputed then to an arbitrary triangle. Dealing with physical matter of simplex coordinates, a general point P inside the triangle subdivides its surface to three partial triangles. Ratio of the surface of a partial triangle, lying opposite to the first node, to the surface of the whole finite element, equals to the coordinate of P on the first simplex coordinate axis (similarly, the second coordinate and the third one can be obtained). Obviously, sum of all the three simplex coordinates equals to one. Small numbers computingAssume a very small scalar value x << 1. Then, following approximate relations are valid:
e.g.
Bessel functions:
Neumann functions:
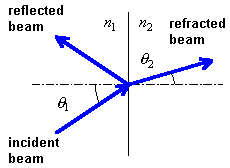
Snell lawSnell law describes the relation between the angle q (under this angle, wave impacts the planar boundary of two media), and the angle q2 (angle between the direction of propagation and the normal to the boundary in the second medium). If refraction index of the first medium is n1 (wave leaves this medium), and refraction index of the second medium is n2 (wave enters this medium), then angles are related by the following equation:
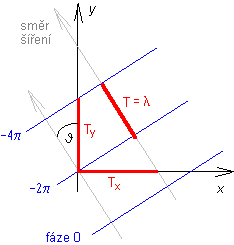
Spatial period, spatial frequencyIn time domain, the term period denoted the shortest time distance (time interval, [s]) of two moments, when phase of harmonic oscillation differs for 2π. In spatial domain, the shortest distance [m] of two points, where phase differs for 2π is denoted as spatial period.
In Figure, plane wave propagation is depicted, and three planar equiphase surfaces, which are perpendicular to the wave propagation, are shown. The symbol T denotes the spatial period in the direction of propagation, and symbols Tx and Ty denote spatial periods in directions of coordinate axes x and y. Unit of the spatial period is [meter]. In the direction of propagation, spatial period equals to the wavelength λ. Inverted value of the spatial period is spatial frequency: f = 1/T,fx = 1/Tx a fy = 1/Ty (in the direction of propagation, in the direction x and in the direction y). The unit is 1/m. Considering Figure, we can see 2πf= ω = 2π /T= 2π/λ = k (wave-number in the direction of propagation), and similarly 2π fy = wy = ky (wave-number in the direction y). Since ky = k cos( j), spatial frequency depends od the direction of propagation. Spatial signal, optic signal, elementary spatial signalSpatial signal (or optic signal) is transmitted by electromagnetic wave. Information is not stored in time course of field intensity but in the amplitude distribution of field intensity in the transversal plane (perpendicular to the direction of propagation): E = E( x, y), z denotes direction of propagation. Amplitude distribution of elementary spatial signal is harmonic in one direction and is constant in another direction. Spectral domain moment methodAssume a frequency selective surface of infinite extent and of periodic position of conductive elements. If such surface is illuminated by a plane wave, then even the distribution of induced currents is periodic. Since spectrum of periodic function is discrete, a continuous current distribution over conductive elements corresponds to the discrete spatial spectrum. Equation for discrete spectra can be simply rewritten to the matrix form, and matrix equations can be solved on the computer. Spectral function, Fourier transform, inverse Fourier transformSpectral function describes frequency dependency of complex amplitudes of spectral components of a signal. Spectral function S( ω) can be computed from a known time course of a signal s(t) using Fourier transform:
On the contrary, time course of a signal can be computed from a known spectral function using inverse Fourier transform
In the above-given relations, S(ω) denotes a spectral function, U(t) is a time course of a signal, ω is angular frequency and t denotes time. Spherical coordinate systemThe system consists of two curvilinear basis vectors j0, j0 and a single direct basis vector r0. Basis vectors are mutually perpendicular (see Figure). An arbitrary point in this coordinate system is described by the vector
Differential operators of the spherical coordinate system are described by the following relations:
Spherical waveEquiphase surfaces of a spherical wave are spherical surfaces. Their common center is called the phase center of a source. Spherical wave can be observed near a point radiator in free space (small antennas). Wave of real (large) sources is not spherical. However, assuming increasing distance from the source, the wave becomes spherical. In a free lossless medium, amplitude of the field intensity of the spherical wave is inversely proportional to the distance from the source. Standing waveIf at least two coherent waves propagate in different directions, then they mutually interfere. In some regions, their phase is permanently identical, intensities are summed and the total intensity is high. In other regions, their phase is not identical, and the sum of intensities is lower. The total field intensity differs from region to region. The variation is not monotonous, and even the phase does not change equably. In the space, the standing wave appeared. Regions of the lowest amplitude of field intensity are called nodes, and regions of the highest intensity are called loops. Standing waves can be observed in media where wave reflection appears (inhomogeneous medium). The forward wave interferes with the backward one. Their propagation directions differ in 180 degrees. Standing wave lengthStanding wave length denotes the shortest distance between two neighboring points, where wave is of the maximally possible amplitude. Similar definition can be stated using minima of amplitudes (nodes). Surface wavesSurface waves are guided by the boundary between two media. Surface waves propagate along this boundary. Surface waves can be observed at the boundary of air and earth surface or at microstrip transmission lines, where the wave does not propagate along the microstrip conductor. Amplitude of surface waves exponentially decreases in the direction, which is perpendicular to the boundary. Symmetric dipoleSymmetric dipole is an antenna consisting of two linear arms of the same length and the same axis. Arms are separated by a small gap, which is used for the excitation of the antenna. Transmission line methodThe above-given term denotes the method of analyzing a complex object (antenna, e.g.) by applying theory of transmission lines. That way, radiation of patch antennas can be computed, e.g. (radiating edges of patches are replaced by slot lines). The method excels in simplicity on one hand, and enables to reach relatively accurate results on the other hand. Transversal electromagnetic waveThe term transversal electromagnetic wave (TEM) denotes the wave, which electric field intensity components and magnetic field ones are perpendicular to the propagation direction. Such wave propagates along the coaxial transmission line e.g.: components of electric-field intensity are oriented in radial direction, components of magnetic-field intensity form rings between the internal conductor and external one. In general, TEM waves propagate along transmission lines consisting of two or more conductors in a homogeneous medium. Although the microstrip transmission line consists of two wires (strip and ground plate), TEM wave does not propagate along because the medium is not homogeneous (dielectric substrate is of different parameters than the vacuum above the strip). Since TEM wave does not enable to meet boundary conditions on the border dielectrics-vacuum, the wave has to contain even longitudinal components. Traveling waveIf wave propagates in the infinite, totally free space, the wave is of traveling nature. In the propagation direction, the phase of oscillations is equably retarded for k' radians per meter. Wave amplitude can be constant (in lossless medium) or can monotonously decline (in lossy medium). Uniform plane wave, non-uniform plane waveThe term uniform plane wave denotes a wave, which amplitude is constant on the equiphase surface. In case of non-uniform wave, amplitude vary on the waveform. Vector potentialWe introduce vector potential A in order to identically meet the fourth Maxwell equation
Since divergence of curl operation equals to zero, vector potential is defined as
Distribution of potential A uniquely determines the field B. On the contrary, a given field B is not uniquely related to a single potential A. If (1) if valid for a vector A, then the same relation is valid even for all vectors A '=A + grad y, where y is an arbitrary scalar function (curl of gradient identically equals to zero). The described ambiguity can be eliminated if an additional condition is formulated for A. Introduction of such condition is called calibration of a potential. Physical notion of vector potential A is described by a relation defining the magnetic flux through the surface S
Obviously, the magnetic inductive flux through the surface S equals to the circulation of vector potential along the boundary curve of this surface. Wave diffraction, diffraction taskIf the wave illuminates an obstacle, which does not contain relatively large, planar and smooth surface, wave reflection does not appear in this situation. On the other hand, the obstacle significantly influences wave propagation. The respective electromagnetic phenomenon is called diffraction. We can imagine that wave trajectories are curved near the obstacle, and therefore, the wave appears even behind the obstacle (even if the obstacle does not transmit the wave). As diffraction, even the other phenomena are explained although the trajectory curvature is not obvious at the first sight (e.g., some cases of guiding waves). In all the situations, the electromagnetic wave mutually interacts with some substantial object of different electrical parameters (permittivity, conductivity, permeability). Wave dispersionThe term dispersion describes the phenomenon when signals on different frequencies propagate by different velocities. Different frequency components are of different delays at the output, and therefore, they represent a signal, which differs from the input one (signal is distorted). Wave equationWave equation is second-order differential equation for the intensity vector of electric field or the magnetic one. If field intensities meet wave equation, the field is of the form of wave. Considering intensity of harmonic electric field, wave equation is of the form
Here, ∇ is differential operator (in Cartesian coordinates, ∇f = [∂f/∂x; ∂f/∂y;∂f/∂z]), E is the vector of electric field intensity, k denotes wave number, ω is angular frequency of harmonic wave, μ denotes permeability of the medium and Jvn is source current exciting wave. Dealing with the intensity of harmonic magnetic field, wave equation is of the similar form. Homogeneous wave equation is of the zero right-hand side (i.e., no source current appears here). Homogeneous wave equation describes the wave in a long distance from the source, where the influence of the source is negligible, and where wave becomes the source of another wave. Wave polarizationPolarization describes the orientation of the electric field intensity vector of an electromagnetic wave. If wave propagates in free space, linear or elliptic polarization can exist. The wave is linearly polarized if the vector E is oriented to the same direction during the whole time period. If an arrow represents instantaneous intensity vector, then its length changes from zero to maximum and back during the half-period. During the second half-period, the described phenomenon repeats with an opposite polarity. The ending point of the arrow moves along a line. If the wave is of elliptic polarization, then the electric field intensity vector changes its direction during the time period. The arrow representing the instantaneous intensity vector rotates during the period, and at the same time, changes its length that way, that the ending point moves along the ellipse. The ellipse is run around within one period exactly. In a special case, the ending point can move along the circle (circular polarization). Elliptic (circular) polarization can be of clockwise or anti-clockwise nature. The sense of rotation is determined from the direction of wave propagation. Elliptically polarized wave can be understood as a superposition of two coherent linearly polarized waves, which vectors E oscillate in different directions and a non-zero mutual shift. If the wave propagates near the plane of boundary of two media, we distinguish between the perpendicular polarization and the parallel one. Let us define the plane of incidence: it is a plane, which is perpendicular to the plane of boundary, and at the same time, is parallel to the wave propagation. The vector E of the perpendicularly polarized wave is perpendicular to the plane of incidence. The vector E of the parallel-polarized wave is parallel to the plane of incidence. If the plane of boundary is identical with the earth surface, then the perpendicularly polarized wave is denoted as horizontally polarized, and the parallel-polarized wave is called vertically polarized one. Wave reflectionReflection of a wave is caused by the incidence of a wave on satisfactorily large and perfectly smooth planar boundary between two media of different electrical parameters. Wave scatteringIf the boundary between two media is not perfectly smooth (is rough), then the incident wave ”reflects” in different areas to different directions. This phenomenon is called scattering and the wave appearing on the rough surface is called the scattered wave. The term scattering denotes even the appearance of a new wave on a very high number of randomly situated particles or facets, which are illuminated by an incident wave in the same moment. As an example, scattering on a large set of raindrops can be given. Wave vector, wave-numberIn a lossless medium, wave number specifies the phase change [radians] of a propagating wave on the one-meter long trajectory in a given direction. Therefore, wave number is given in radians per meter. Wave number is associated with the wavelength k = 2π/λ and with the phase velocity of propagation k = ω/vf. If wave-number k is associated with the direction of wave propagation, then both the wavelength and the phase velocity are associated with the direction of wave propagation. If another direction is considered, the above-given relations stay valid, but all the three quantities are associated with the given direction. In the direction of propagation, wave number is of the highest value, wavelength and phase velocity are of the lowest one. In a lossy medium, wave number is complex. Its real part k' gives the phase change of wave on the one-meter long trajectory as already explained. Imaginary part (when sign is changed) k'' gives the specific wave attenuation. The wave amplitude decreases on the trajectory of the length r for where k'' is imaginary part of wave-number in the direction r. Magnitude of the wave vector is identical with the magnitude of wave number. Direction of the wave vector is identical with the direction of wave propagation. If projections of wave vector to various directions are computed, then wavelength and phase velocity for those directions can be determined. WaveguideThe term waveguide denotes a hollow metallic tube, which transversal dimensions are comparable to the wavelength. Wave propagation in a waveguide can be interpreted as sequential reflections from the walls of the waveguide. In the transversal directions, a standing wave appears (in different points of the cross-section, different amplitudes of field intensities can be measured). WavelengthWavelength is the shortest distance between two points, where wave is of the same phase. Weighting function, residuum, method of weighting residuaIf approximation of the solution is substituted to the solved equation, the solved equation is not met exactly. This fact is respected by adding a residual function to the right-hand side of the equation. In order to minimize the residual function (i.e., in order to get as accurate approximation as possible), the residual function is multiplied by a weighting function, the product is integrated over the whole analyzed structure and the result is put to equal zero. This algorithm is called the method of weighted residua. Wire dipoleThe dipole is a direct segment of a conductor, which is interrupted by a feeding gap in the center. If a symmetric source of the harmonic voltage is connected to the gap, then in the first half-period, a current flows to one arm, and charges of the current concentrate at the end of the arm. In the second half-period, accumulated charges flow back to the source. In the second arm, the situation is similar (in the first half-period, accumulated charges flow back to the source, in the second half-period, the charges accumulate). Dealing with the wire dipole, a circular profile and a small radius (with respect to the wavelength) of the antenna wire are assumed. Yagi antenna, reflector, directorYagi antenna consists of a single active element and several passive ones. The role of the active element is usually played by a symmetric (or folded) dipole operating in one-quarter-wavelength resonance. Passive elements are dipoles without the excitation gap. One passive element, which is longer than the active one, is positioned behind the active element and plays the role of the reflector. The other passive elements are shorter than the active one, are positioned in front of the active element, and are called directors. |