3 Optimality conditions - examples

Using examples, we are going to demonstrate the way how can be tested optimality of a given point. For simplicity, we start with a single-variable function, and further, we extent our approach to a two-variable function.

3.1 Single-Variable Function

Assume the following function :

(3.1)

The function is expected to have minims in points x1 = -1, x2 = 0 and x3 = +1. We are aimed to verify it.

First, the stationarity condition has to be verified. Hence, we compute the first derivative of (3.1)

(3.2)

and we evaluate it for x1, x2 and x3. Whereas the value of the first derivative is zero in the first point and in the third one, the value in the second point equals to -2. Whereas the first-order optimality condition is met in x1 and x3, in x2 this condition is not met, and the objective function cannot have minimum in that point.

In the next step, we have to decide whether the objective function have minims, maxims or inflexions in x1 and x3. We therefore compute the second derivative of the objective function

(3.3)

and evaluate it in points x1 and x3. In both the cases, we come to the value +802. The positive value of the second derivative proves the minims in the points x1 and x3.

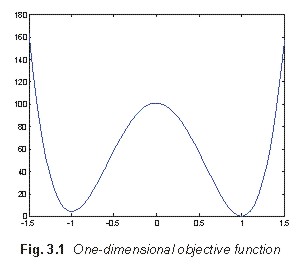
Correctness of the computation is illustrated by Fig. 3.1, which shows the function (3.1) near the origin of the coordinate system. We can see that minims really appear in the points x1 and x3 and that there is a maximum in a small distance from x2.

3.2 Two-Variable Function

Assume the following function :

(3.4)

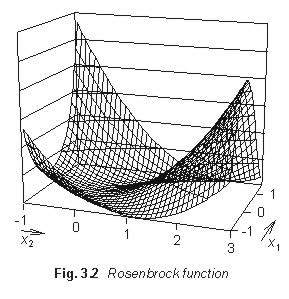
The function (3.4) is called Rosenbrock one. Rosenbrock function describes a banana-shaped valey of steep slopes in one direction and of a flat bottom in other direction. From the optimization viewpoint, such functions are difficult to be minimized, and therefore, Rosenbrock function is used for testing properties of optimization methods. Rosenbrock function near the origin of the coordinate system is depicted in Fig. 3.2.

We are aimed to verify if the minimum of Rosenbrock function is in the point [1, 1].

In order to verify the first-order optimality condition, we have to compute the gradient of the objective function (3.4)

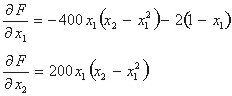(3.5)

Substituting x1 = 1 and x2 = 1 in (3.5), both the components of the gradient become zero. The norm of the gradient is therefore zero in [1, 1], and hence, we can expect a minimum, a maximum or a saddle point there. In order to decide, which of the three-listed cases corresponds to the point [1,1], we have to compute Hess matrix

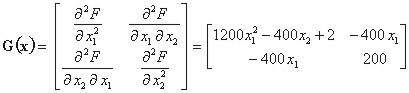(3.6)

We substitute x1 = 1 and x2 = 1 to (3.6) and evaluate eigenvalues of Hess matrix in MATLABu using the function eig: k1 = 1001,6 and k2 = 0,4. Both the eigenvalues are positive, Hess matrix is positive definite, and there is a minimum of Rosenbrock function in [1,1].

3.3 When the Derivatives are Unknown ...

When solving practical optimization problems, derivatives can be computed analyticaly in the expected optimal point exceptionally. When designing an antenna, e.g., its numerical model stays at our disposal in the computer, which is able to produce a current distribution on antenna metallic parts and field distribution on antenna apertures for given frequency and given dimensions of the antenna. In a fact, the numeric model maps dimesnions as state variables to electric quantities as parameters of the optimization problem. An analytic expression of the objective function is not known, and therefore, the gradient and the Hess matrix have to be computed numerically.

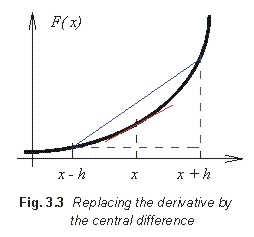
The numeric evaluation of the gradient is based on replacing derivatives by central differences (Fig. 3.3). When computing the value of the first derivative in the point x, we are interested in the direction of the red tangent. Doing a side-step h above the value x, and a side-step h below the value x, we create the blue rectangular triangle, which hypotenuse is of the direction close to the direction of the tangent. The correspondence of both the directions is better and better when the length of the side-step h is smaller and smaller. Mathematically, the substitution of the derivative by the central difference can be expressed by the following way:

(3.7)

The eqn. (3.7) shows us, that the length of the side-step cannot be arbitrarily shortened: when dividing by a very small number, the numeric error of the computation significantly rises.

When computing a second derivative by central differences, the computation is divided into two steps:

- using differences, we compute first derivatives in the points x-h and x+h

(3.8)

- forming a central difference from (3.8), we create the second derivative estimate in x.

Working with central differences, we have to carefully consider points, where the estimate of the derivative is valid.

Now, the above-described method is going to be illustrated by an example. In the Matlab file rosenbrock.m, Rosenbrock function (3.4) is stored. The content of the file is assumed to be unknown, and the file is expected to provide a functional value on the basis of input parameters x1 and x2 only. We are again aimed to verify, whether there is the minimum in the point [1,1] or not.

Let us start with the stationarity condition, and express components of the gradient using central differences cond01.m:


function g = cond01( x)

h = 1e-6;

X1(1,1) = rosenbrock( [x(1,1) + h; x(2,1)]);
X1(2,1) = rosenbrock( [x(1,1) - h; x(2,1)]);

X2(1,1) = rosenbrock( [x(1,1); x(2,1) + h]);
X2(2,1) = rosenbrock( [x(1,1); x(2,1) - h]);

g(1,1) = (X1(1,1) - X1(2,1)) / (2*h);
g(2,1) = (X2(1,1) - X2(2,1)) / (2*h);

When evaluating the first component of the gradient, we operate the first variable only, and second variable stays constant. When evaluating the second component of the gradient, the approach is similar. Using the side-step h = 10-6, components of the gradient are smaller than 10-10. Using the side-step h = 10-8, components of the gradient are smaller than 10-13. We can therefore conclude: the norm of the gradient approaches zero when decreasing the length of the side-step h. Therefore, the stationarity condition can be considered to be met.

Let's turn our attention to the optimality condition cond02.m:


function g = cond02( x)

h = 1e-8;

X1(1,1) = rosenbrock( [x(1,1) + 2*h; x(2,1)]);
X1(2,1) = rosenbrock( [x(1,1) ; x(2,1)]);
X1(3,1) = rosenbrock( [x(1,1) - 2*h; x(2,1)]);

f1 = (X1(1,1) - X1(2,1)) / (2*h);
f2 = (X1(2,1) - X1(3,1)) / (2*h);

G(1,1) = (f1 - f2) / (2*h);

X2(1,1) = rosenbrock( [x(1,1); x(2,1) + 2*h]);
X2(2,1) = rosenbrock( [x(1,1); x(2,1)]);
X2(3,1) = rosenbrock( [x(1,1); x(2,1) - 2*h]);

f1 = (X2(1,1) - X2(2,1)) / (2*h);
f2 = (X2(2,1) - X2(3,1)) / (2*h);

G(2,2) = (f1 - f2) / (2*h);

X3(1,1) = rosenbrock( [x(1,1) + h; x(2,1) + h]);
X3(2,1) = rosenbrock( [x(1,1) + h; x(2,1) - h]);
X3(3,1) = rosenbrock( [x(1,1) - h; x(2,1) + h]);
X3(4,1) = rosenbrock( [x(1,1) - h; x(2,1) - h]);

G(1,2) = (X3(1,1) - X3(2,1) - X3(3,1) + X3(4,1)) / (2*h)^2;
G(2,1) = G(1,2);

g = eig( G);

In the first two blocks, we compute the second derivative according to x1, and the second derivative according to x2. That way, we obtain the elements G(1,1) and G(2,2) of Hess matrix. The computation follows the above-descried approach (see eqn. 3.8).

Elements G(1,2) and G(2,1) of Hess matrix are evaluated according to

(3.9)

When the side-step is set to h = 10-8, the numerical computation provides results, which are identical with the analytical computation.