4.4 Metoda nejmenších čtverců

V mnoha případech má kriteriální funkce F(x) charakter součtu kvadrátů (čtverců) nelineárních funkcí

(4.17)

Potom lze gradient a hesián vyjádřit ve speciálním tvaru. Tento speciální tvar vychází z tvz. jakobiánu (Jacobiho matice). Pro případ naší kriteriální funkce (4.17) můžeme jakobián vyjádřit následovně:

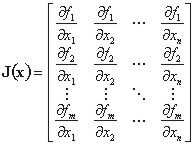
(4.18)

V prvním řádku jakobiánu vystupují parciální derivace první funkce podle všech proměnných, v m-tém řádku derivujeme podle všech proměnných funkci m-tou.

Máme-li takto vypočten jakobián, lze gradient vyjádřit vztahem

(4.19a)

a hesián vztahem

(4.19b)

kde

(4.19c)

a f(x) = [f₁(x) f₂(x) ... f_m(x)]^T.

Tohoto speciálního vyjádření pak využívají různé optimalizační metody k tomu, aby byl algoritmus pro minimalizaci kriteriální funkce co možná nejefektivnější. My se v dalších odstavcích seznámíme s dvěma metodami - metodou Gaussovou-Newtonovou a metodou Levenbergovou-Marquardtovou.

4.4.1 Gaussova-Newtonova metoda

Gaussova Newtonova metoda vychází z předpokladu, že člen J(x)^T . J(x), v němž vystupují pouze parciální derivace prvého řádu, dominuje nad členem Q, který má v submaticích G ukryty parciální derivace druhého řádu. Dosadíme-li gradient a hesián do Newtonova vztahu (4.13), dostáváme

(4.20)

Ze vztahu (4.20) můžeme určit směr hledání minima p_k. Pokud se vrátíme zpět k našemu předpokladu, že člen s derivacemi prvého řádu dominuje nad členem s derivacemi řádu druhého, vztah (4.20) přejde na

(4.21)

Jak již bylo řečeno, vztah (4.21) obsahuje pouze derivace prvého řádu. Vyřešením (4.21) dospějeme ke Gaussovu-Newtonovu směru p_k.

4.4.2 Levenbergova-Marquardtova metoda

U Levenbergovy-Marquardtovy metody je směr hledání definován jako řešení následující rovnice:

(4.22)

V této rovnici značí I jednotkovou matici a l_k je nezáporný skalár. Zvolíme-li l_k = 0, je řešením (4.22) Gaussův-Newtonův směr hledání minima p_k. Předpokládáme-li, že se l_k blíží k nekonečnu, je směr hledání p_k orientován rovnoběžně se směrem hledání metody nejstrmějšího sestupu.