univariate optimization

4.1 Univariate Optimization

We assume a single minimum of the objective function within the interval <a, b>. Reveling this minimum as accurately as needed is our task.

4.1.1 Fibonacci Search

Fibonacci search is an optimal search strategy (maximal shortening of the original interval for a given number of functional values of the objective function). The strategy is based on Fibonacci numbers {X_i} meeting the condition

(4.1)

If N functional values of the objective function are given then Fibonacci numbers X_N_-1, X_N_-2, ... can define points, where the objective function is evaluated. These points form the sequence of a shortening interval; we start by the initial interval <0, X_N>.

If the initial interval is assumed being <0, X₂> (X₂ = 2), the objective function F is evaluated in two points

(4.2)

Here, d is a very small number eliminating evaluation of the objective function in the same point. No matter what is the value of F( x₁) and F( x₂), the initial interval is shortened to the half of the initial one (see Fig. 4.1). Exploiting N functional values, the initial interval can be shortened to 1/F N of its initial length.

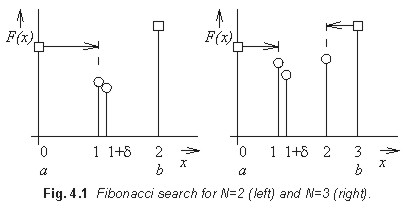
The main disadvantage of Fibonacci search is hidden in the fact that the optimal number of Fibonacci numbers (and therefore, the number of evaluation the objective function) is unknown a priori. This fact complicates meeting the desired accuracy of the search.

4.1.2 Golden Section Search

Golden section search does not require a priori information about the size of the final interval on one hand and exhibits nearly the same efficiency as the Fibonnaci search on the other hand.

We can show that

(4.3)

where t meets the quadratic equation

(4.4)

Iteratively, the objective function is evaluated in points corresponding to t = 0.6180 and (1- t ) = 0.3820, which ensures reduction of the interval of relative length 1 to the interval of the relative length t in every iteration step.

4.1.3 An Example

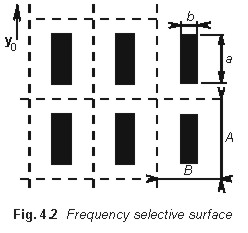In antenna techniques, planar structures called frequency-selective surfaces (FSS) are frequently used as radomes or frequency-selective reflectors. FSS are periodic structures, which can consist, e.g., of equidistantly distributed identical rectangular elements on a dielectric substrate. On given frequencies, FSS behave as a perfect reflector, which reflect all the energy of the incident wave (FSS exhibits the same properties as an continuous metallic reflector). On the contrary, there are frequencies, where FSS behaves as a dielectric layer without any metallic part (most power of the incident wave passed through the FSS to the space behind the structure. These properties are caused by proper phasing of currents induced to patches by the incident wave.

In our example, we assume all the metallic parts of FSS to be perfectly electrically conductive (PEC). The conductive rectangles are positioned in the center of a discrete cell of the infinite plane of the same electrical parameters as the surrounding environment. The height of the conductive element is fixed at the value a = 11 mm, and even the height of the cell is assumed to be constant A = 12 mm. The width of the conductive element is changed within the interval b = <1 mm, 7 mm>, and the width of the cell can intervene between B =<10 mm, 22 mm>.

Exploiting the golden section search, we are going to find such a frequency f within a given interval <f_min, f_max>, where a given FSS of the dimensions a, A, b, and B exhibits the maximum magnitude of the reflection coefficient. Reflection coefficient is computed by the m-file fss2.zip, where the spectral-domain moment-method analysis of FSS is performed. MATLAB source code golden.m of the searching routine is listed below. A detailed description is given in comments.

function out = golden( fmin, fmax, a, A, b, B, D)

% fmin, fmax = frequency interval where the maximum reflection should appear
% a, b = dimensions of a metallic patch of FSS
% A, B = dimensions of a cell of FSS
% D = maximum magnitude of reflection coefficient

tau = 2 / (1+sqrt(5));                       % golden section frequencies
f = fmin + [0; 1-tau; tau; 1]*(fmax-fmin);
mod = fss2( f, a, A, b, B);                  % analyzing FSS on frequencies f

while min( abs(D-mod))>0.005                 % stop if 0.5 per cent accuracy reached

   [rmx,imx] = max( abs( D-mod));            % maximum value of objective function

if imx==1                              % ... on the left
    f( 1:2,1) = f( 2:3, 1);              % left border eliminated
    f( 3, 1) = tau*(f(4,1)-f(1,1)) + f(1,1);
    mod(1:2,1) = mod(2:3,1);             % new golden frequency
    mod(3, 1) = fss2( f(3), a, A, b, B);     % new analysis
end

if imx==4                                  % ... on the right
    f( 3:4,1) = f( 2:3, 1);                  % right border eliminated
    f( 2, 1) = (1-tau)*(f(4,1)-f(1,1)) + f(1,1);
    mod(3:4,1) = mod(2:3,1);                 % new golden frequency
    mod(2, 1) = fss2( f(2), a, A, b, B);     % new analysis
end

end                                          % end of the iteration loop

[rmx,imx] = min( abs(D-mod));
out = f( imx);                               % frequency of the maximum reflect.coef.