2 Základní pojmy - příklady

Význam základních pojmů optimalizace budeme ilustrovat dvěma konkrétními příklady z oblasti elektrotechniky. Prvním příkladem je optimalizace symetrického dipólu, druhým příkladem je optimalizace vlnovodu s příčným profilem ve tvaru H.

2.1 Symetrický dipól

Vlastnosti symetrického dipólu (obr. 2.1) na zadaném kmitočtu f jsou dány jeho délkou l a poloměrem anténního vodiče a. Tyto proměnné jsou tedy proměnnými stavovými, z nichž sestavíme stavový vektor z dvojrozměrného reálného prostoru

(2.1)

Vlastnosti symetrického dipólu budeme posuzovat z hlediska vstupního odporu R(l, a) a vstupní reaktance X(l, a). Při optimalizaci tedy budeme měnit délku a poloměr anténního vodiče tak, abychom dosáhli požadované hodnoty R_d a X_d. Kriteriální funkci tedy můžeme vyjádřit vztahem

(2.2)

Čím menší bude hodnota kriteriální funkce, tím blíže budou aktuální hodnoty vstupního odporu a vstupní reaktance hodnotám požadovaným.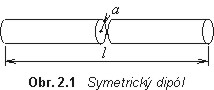

Ze vztahu (2.2) je rovněž vidět, proč rozdíly aktuálních a požadovaných hodnot vstupních parametrů umocňujeme. V opačném případě (bez umocnění) by mohl být velký kladný rozdíl odporů kompenzován velkým záporným rozdílem reaktancí a hodnota kriteriální funkce by nabývala malé hodnoty i v případě, kdy se nacházíme daleko od optima. 

Pokud bychom chtěli kriteriální funkci (2.2) zařadit z hlediska klasifikace optimalizačních problémů, jak bylo uvedeno ve vrstvě A, bude se jednat o součet čtverců nelineárních funkcí (závislost vstupního odporu a vstupní reaktance na rozměrech dipólu je nelineární).

Při hledání takových rozměrů dipólu, který bude mít na daném kmitočtu vstupní impedanci, jež je v ideálním případě rovna vstupní impedanci požadované, minimalizujeme kriteriální funkci (2.2)

(2.3)

Jelikož rozměry a a l nemohou být záporné, doplníme neomezenou optimalizaci (2.3) omezujícími podmínkami

(2.4a)

Tyto podmínky nazýváme prostým omezením nerovností (viz klasifikace omezujících podmínek ve vrstvě A).

Aby si anténa uchovala charakter dipólu, musí být délka antény l mnohem větší než poloměr vodiče a (v opačném případě bychom dostali deskový kondenzátor s kruhovým tvarem elektrod). Požadujeme-li alespoň 100-krát větší délku antény vzhledem k poloměru vodiče, musíme přidat další omezující podmínku

(2.4b)

Podmínku (2.4b) můžeme klasifikovat jako omezení lineární nerovností. Přípustná oblast optimalizace, vymezená podm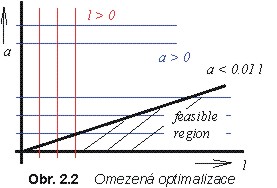ínkami (2.4), je vyznačena na obr. 2.2. Optimální hodnoty stavových proměnných a a l tedy nehledáme v celé rovině [a, l], ale omezujeme se pouze na šrafovaný klínový výřez. Tím jsme podstatně zmenšili oblast, kterou při hledání optima prohledáváme.

Další omezení, jímž bychom přípustnou oblast ohraničili na oblast konečných rozměrů, by spočívala v definování maximálních možných rozměrů, jichž anténa může nabývat. Tato omezení zde však pro jednoduchost již neuvádíme.

Nyní se pokusíme celý náš optimalizační problém přepsat do maticového tvaru, který bude odpovídat vztahům (2.4) v základní vrstvě.

Prostá omezení (2.4a) můžeme vyjádřit vztahy

(2.5a)

Lineární omezení (2.4b) pak můžeme přepsat do tvaru

(2.5b)

Jelikož naše omezení jsou lineární, mají funkce c₁, c₂ a c₃ charakter vektorů koeficientů c₁ = [0, 1], c₂ = [1, 0] a c₃ = [0.01, -1] .

Tím je náš první příklad u konce mělo by z něj být zřejmé, jaký je konkrétní význam základních pojmů z oblasti optimalizace.

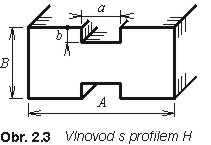
2.2 Kovový vlnovod s profilem H

Nyní si všechny kroky, popsané v odstavci 2.1, zopakujeme pro formulaci optimalizace dutého kovového vlnovodu s příčným profilem ve tvaru písmene H (obr. 2.3). Pro jednoduchost budeme předpokládat, že vlnovod je vyroben z dokonalého elektrického vodiče (PEC, perfect electric conductor) a že uvnitř vlnovodu je vakuum. Dále předpokládáme, že vlnovod je nekonečně dlouhý a jeho parametry se v podélném směru nemění (říkáme, že vlnovod je podélně homogenní). Vnější rozměry vlnovodu jsou shodné s rozměry vlnovodu R100, tj. A = 22,86 mm a B = 10,16 mm. Při optimalizaci budeme měnit šířku prolisu a a jeho výšku b tak, abychom dosáhli jednovidovosti vlnovodu v předepsaném pásmu kmitočtů. Pásmo jednovidovosti je dáno kritickým kmitočtem dominantního vidu TE10 (od této frekvence se vlnovodem začíná šířit elektromagnetická vlna) a kritickým kmitočtem druhého vyššího vidu TE20 (od této frekvence se vlnovodem začínají šířit různou rychlostí dvě vlny, které se vzájemně skládají).

Kriteriální funkci budeme formulovat jako součet čtverců rozdílů mezi aktuální hodnotou kritického kmitočtu vidu TE10 f₁₀(a, b) a hodnotou požadovanou f_10,d, a dále mezi aktuální hodnotou kritického vidu TE20 f₂₀(a, b) a hodnotou požadovanou f_20,d

(2.6)

Z hlediska klasifikace se opět jedná o součet čtverů nelineárních funkcí.

Kriteriální funkci budeme minimalizovat vzhledem k rozměrům prolisu a, b

(2.7)

Z rozměrů prolisu sestavíme stavový vektor

(2.8)

Minimum kriteriální funkce tedy budeme opět hledat ve dvojrozměrném reálném stavovém prostoru, nyní [a, b]. Stavový prostor však musíme stejně jako u dipólu omezit. Šířku prolisu a budeme měnit od hodnoty 0 mm (vlnovod nemá žádný prolis) do hodnoty 18 mm (nožička písmene H je tlustá 4,86 mm). Výšku prolisu b měníme od hodnoty 0 mm (bez prolisu) do hodnoty 4 mm (tloušťka příčky v písmenu H je 2,16 mm). Dostáváme tedy prostá omezení, která můžeme v maticové formě vyjádřit vztahy

(2.9)

V případě vlnovodu s příčným profilem ve tvaru písmene H tedy hledáme minimum kriteriální funkce (2.6) v obdélníkové přípustné oblasti o konečné ploše 18 mm x 4 mm.

Tím je formulace optimalizačního problému hotova. Nyní stačí vybrat vhodnou metodu minimalizace a najít v přípustné oblasti optimum. O metodách neomezené optimalizace (tj. minimalizace bez omezujících podmínek) pojednává 4. kapitola.