2 Základní pojmy

Co je to vlastně optimalizace? Je to proces hledání toho nejvhodnějšího (optimálního) řešení, té nejkratší (optimální) cesty, nákup co možná nejlevnějšího a současně nejkvalitnějšího (optimálního) zboží.

Při optimalizaci měníme tzv. stavové proměnné optimalizovaného objektu a sledujeme, jaký vliv má změna těchto proměnných na výsledné parametry. Připravujeme-li jídlo, mohou hrát roli stavových proměnných (určují stav jídla) hmotnosti jednotlivých ingrediencí. Sledovaným parametrem jídla může být jeho chuť. Optimalizátor - kuchařka - tak dlouho mění množství přísad, dokud nedosáhne požadované chuti.

Optimalizací tedy rozumíme hledání takových hodnot stavových proměnných (state variables ) systému, které zajistí, že systém bude dosahovat požadovaných parametrů nebo že se parametry systému budou co možná nejvíce blížit parametrům žádaným.

Odchylka aktuálních parametrů systému (nedochucené jídlo) od parametrů žádaných (ideální chuť) v závislosti na stavových proměnných systému (množství ingrediencí) je popisována kriteriální (účelovou, chybovou) funkcí (criterial, cost, error function) . Samotnou optimalizaci pak lze chápat jako hledání minima nebo maxima kriteriální funkce změnou hodnot stavových proměnných.

Označme stavové proměnné optimalizovaného systému symboly x₁, x₂, ..., x_n, parametry optimalizovaného systému y₁, y₂, ..., y_m a žádané hodnoty těchto parametrů d₁, d₂, d_m. Obecný optimalizační problém pak lze popsat jako minimalizaci

(2.1)

Kriteriální funkci můžeme vyjádřit jako součet kvadrátů odchylek mezi aktuálními hodnotami parametrů a hodnotami požadovanými

(2.2)

Aktuální hodnota parametrů optimalizovaného systému, a tudíž i hodnota minimalizované kriteriální funkce, závisejí na stavovém vektoru (sloupcový vektor stavových proměnných)

(2.3)

Ve vztahu (2.1) předpokládáme, že prvky stavového vektoru jsou reálná čísla (vektor x je prvkem n-rozměrného reálného prostoru).

Optimalizační problém (2.1) nazýváme neomezenou optimalizací (unconstrained optimization ), tzn. že prvky stavového prostoru se mohou během optimalizace měnit bez jakýchkoli omezení. V praktických situacích tomu ovšem tak není: při ochucování jídla mohou být hmotnosti jednotlivých ingrediencí pouze kladné a navíc nemohou nabývat neomezeně velké hodnoty. V takových případech hovoříme o optimalizaci omezené omezujícími podmínkami (constrained optimization ).

Omezující podmínky můžeme obecně vyjádřit vztahy

	(2.4a)
	(2.4b)

Podmínku (2.4a) nazýváme omezením rovností (equality constraint ). Omezení říká, že stavová proměnná nebo funkce stavových proměnných (lineární či nelineární) musí být rovna nule. Definujeme k' omezení rovností.

Podmínka (2.4b) je omezením nerovností (inequality constraint ). Zde vyjadřujeme, že stavová proměnná nebo funkce stavových proměnných (lineární či nelineární) musí být větší nebo rovna nule Vynásobíme-li obě strany koeficientem -1, dostáváme podmínku, že stavová proměnná nebo funkce stavových proměnných je menší nebo rovna nule.

Soustavu vztahů (2.1), (2.4a) a (2.4b) nazýváme nelineárně omezený problém (NCP, non-linearly constrained problem). V podstatě je jedná o nejobecnější optimalizační problém. Konkrétní příklady uvádíme ve vrstvě B v české verzi a ve vrstvě C ve verzi anglické.

2.1 Klasifikace optimalizačních úloh

Jak bylo vysvětleno v předchozích odstavcích, formulace optimalizačního problému spočívá jednak ve formulaci samotné kriteriální funkce a jednak ve formulaci omezujících podmínek. Při klasifikaci optimalizačních úloh tedy musíme brát v potaz jak charakter omezujících podmínek tak charakter kriteriální funkce. Potom lze optimalizační problémy klasifikovat, jak je uvedeno v tab. 2.1.

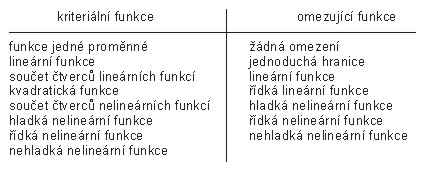
Tab. 2.1 Klasifikace optimalizačních úloh dle charakteru
kriteriální funkce a omezujících podmínek

Nejjednodušším případem je kriteriální funkce jedné proměnné (během optimalizace měníme hodnotu jediné stavové proměnné). Pro minimalizaci takové funkce (je-li hladká a spojitá) můžeme použít přístupy známé ze základních kursů matematiky. Není-li funkce hladká a spojitá, lze využít vyhledávání minima, které je založeno na Fibonacciho číslech. Tyto vyhledávací metody jsou popsány v podkapitole 4.1.

O něco složitějším případem je lineární funkce N proměnných (rovina v N-rozměrném prostoru). Sama lineární kriteriální funkce má minimum v nekonečnu, takže její neomezená optimalizace nedává smysl. Pokud však lineární kriteriální funkci doplníme sadou omezujících podmínek, musíme hledat nejníže položený bod na hranici přípustné oblasti. V případě lineární kriteriální funkce je takové hledání opět relativně snadné.

O něco komplikovanějším případem je součet čtverců lineárních funkcí. V podstatě je jedná o součet paraboloidů v N-rozměrném lineárním prostoru, jehož výsledkem je opět paraboloid. Paraboloid má jedno dobře definované minimum, do něhož se monotónně svažují stěny paraboloidu. Sklouznutí po stěně do minima lze opět relativně jednoduše realizovat. Do stejné kategorie složitosti lze rovněž zahrnout minimalizaci kvadratických funkcí.

Součet čtverů nelineárních funcí je problémem, který jsme na dvou aplikačních případech vysvětlili ve vrstvě B a ve vrstvě C. Proto na tomto místě další vysvětlování vynecháme. Pouze si uvědomme, že vzhledem k nelineárnímu charakteru minimalizovaných funkcí vzniká řada lokálních minim, která musíme při hledání minima globálního ignorovat. Termíny lokální minimum a globální minimum vysvětlíme v odstavci 2.2.

Hladnou nelineární funkcí je obecná nelineární funkce, která je spojitá a má spojitou první a druhou derivaci. Vzhledem k obecnosti této funkce nelze učinit speciální předpoklady jako u součtu čtverců nelineárních funkcí, což minimalizaci komplikuje.

Zbývající dva typy kriteriálních funkcí patří mezi nejkomplikovanější optimalizační problémy. Řídká nehladká nelineární funkce je funkcí, která vykazuje nespojitosti. Vzhledem k těmto nespojitostem lze k minimalizaci funkce použít pouze srovnávací metody - počítáme hodnotu kriteriální funkce v několika bodech N-rozměrného prostoru, najdeme oblast nejnižších funkčních hodnot kriteriální funkce a v této oblasti se snažíme hledat body s ještě nižší funkční hodnotou.

Co se týký efektivnosti optimalizačních metod, ta je nejvyšší v případě jedné proměnné a směrem k nehladké nelineární funkci klesá. Zatímco metody pro minimalizaci nehladkých nelineárních funkcí mají obecnou platnost (lze je použít i pro minimalizaci funkce jedné proměnné, i když s mizernou efektivitou), metody pro minimalizaci jednodušších kriteriálních funkcí nelze použít v případě funkcí složitějších. Metody pro minimalizaci kvadratických funkcí mohu použít pro minimalizaci funkce jedné proměnné, ale nemohu ji aplikovat na minimalizaci nelineární nehladké funkce.

Je tedy zřejmé, že správná klasifikace optimalizačního problému hraje důležitou roli. Umožňuje nám totiž vybrat tu nejefektivnější metodu minimalizace, která nás dovede k cíli.

Obdobným způsobem jsou v tabulce řazeny omezující podmínky. Nejjednodušším omezením je omezení žádné. O něco komplikovanějšími omezeními jsou jednoduché hranice a lineární omezení, jak bylo vysvětleno ve vrstvě B a ve vrstvě C na aplikačních příkladech. Zatímco při omezení lineární funkcí definujeme přímé hranice přípustné oblasti, v případě omezení nelineární funkcíjsou hranice přípustné oblasti křivočaré. Komplikovanějšími hranicemi se nebudeme zabývat.

2.2 Klasifikace optimalizačních metod

Stejně jako optimalizační úlohy můžeme klasifikovat optimalizační metody. Způsobů dělení metod optimalizace je celá řada. My si zde uvedeme pouze dělení na globální metody a metody lokální. Nejprve si však vysvětleme pojmy lokální a globální optimum.

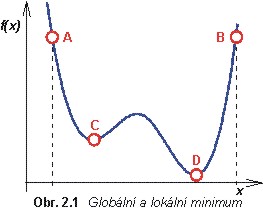
Na obr. 2.1 je nakreslen možný průběh minimalizované kriteriální funkce. Pokud minimum definujeme jako bod, od nějž nalevo i napravo kriteriální funkce roste, můžeme termínem minimum označit jak bod C tak bod D. Minimum, v němž kriteriální funkce nabývá nejmenší funkční hodnoty (v našem případě D), nazveme minimem globálním. Minima, v nichž je funkční hodnota větší, nazveme minimy lokálními (v našem případě C).

U metod, které kloužou po průběhu funkce tak dlouho, dokud se nedostanou do minima, může dojít k uváznutí v minimu lokálním, i když globální minimum nemusí být daleko. Vezmeme-li jako počáteční bod optimalizace bod A, dojde k právě popsanému uváznutí v lokálním minimu C. Pokud však optimalizaci zahájíme v bodě B, metody dospějí do globálního minima B.

Popsaná vlastnost je typická pro lokální optimalizační metody. Metody globální jsou naproti tomu schopny překonat lokální minima a přiblížit se k minimu globálnímu. Nevýhodou globálních metod je nesrovnatelně vyšší výpočetní náročnost.

Tím končí kapitola, která se věnovala vysvětlení základních pojmů z oblasti optimalizace a která popsala klasifikaci optimalizačních problémů a optimalizačních metod.